【bzoj2238】Mst(树链剖分+线段树)
2238: Mst
Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 465 Solved: 131
[Submit][Status][Discuss]
Description
给出一个N个点M条边的无向带权图,以及Q个询问,每次询问在图中删掉一条边后图的最小生成树。(各询问间独立,每次询问不对之后的询问产生影响,即被删掉的边在下一条询问中依然存在)
Input
第一行两个正整数N,M$(N<=50000,M<=100000)$表示原图的顶点数和边数。
下面M行,每行三个整数X,Y,W描述了图的一条边$(X,Y)$,其边权为W$(W<=10000)$。保证两点之间至多只有一条边。
接着一行一个正整数Q,表示询问数。$(1<=Q<=100000)$
下面Q行,每行一个询问,询问中包含一个正整数T,表示把编号为T的边删掉(边从1到M按输入顺序编号)。
Output
Q行,对于每个询问输出对应最小生成树的边权和的值,如果图不连通则输出“Not connected”。
Sample Input
4 4
1 2 3
1 3 5
2 3 9
2 4 1
4
1
2
3
4
1 2 3
1 3 5
2 3 9
2 4 1
4
1
2
3
4
Sample Output
15
13
9
Not connected
13
9
Not connected
数据规模
10%的数据$N,M,Q<=100$。
另外30%的数据,$N<=1000$。
100%的数据如题目。
另外30%的数据,$N<=1000$。
100%的数据如题目。
第一眼看题以为是求最小生成树再加一条最小边,组成最小与次小生成树的合并(即n个点n条边),然后删的边如果在生成树里,就输出生成树的边权和减去这条边,如果不在生成树里,就输出最小生成树的边权和。
然而这个做法很快被 パス 掉了(bzoj的题显然没这么简单),因为删去一条树边仍然可能使原图不连通。因此,这题不是让求次小生成树。
经过dalao指导,发现这是数据结构板子题。
尽管这题不是让求次小生成树,但我们依然可以借鉴其某些思路。
我们先做好图的最小生成树。
如果删除的边不在最小生成树上,那答案没变,直接输出即可。
所以下文讨论的 均是删除的边在最小生成树上的情况。
此时要找能够代替 删去的边 的一条权值最小的边。用这条边代替删去的边后就是新的最小生成树了。
那怎么代替呢?
我们把最小生成树的样子画个图看看
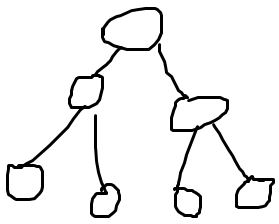
我们容易发现它作为一棵树的性质:删去任意一条边只会把树分成两个连通块。我们要找的是所有 能使两个连通块连通的 非树边。这样的非树边就能够代替删去的边重新使树连通。
那怎么维护 能够代替删去的边的一条权值最小的边?(本题只要求最小生成树的权值和,因此可以只维护所需边的权值)
随便举个栗子:

红叉是删除的边,橙/绿线是非最小生成树的原图边。
很容易发现,这些橙边都可以成为代替边,而绿边都不可以成为代替边。直观原因是橙边都连接了两个连通块,而绿边都没有连接。
那反过来想,一条非树边可以代替哪些边?
找找简单情况(下面的图中黑边都是树边):
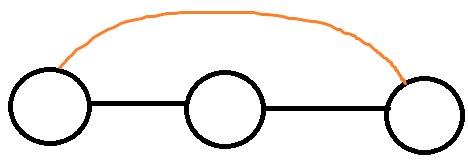
很明显,这条橙边可以代替两条黑边中的任意一条。
我们往左边拓展一点

也很明显,橙边只能代替右边两条黑边而不能代替最左边的黑边,绿边只能代替最左边的黑边而不能代替右边两条黑边。
这时结论就出来了:一条非树边可以代替其两端点在树上的简单路径之间的所有边
证明:

以这个图为例,一条非树边与其两端点在树上的简单路径组成的是一个x个点x条边的环,而这x个点可以删去其中一条边,只用x-1条边连通,因此这条非树边可以代替简单路径中的任意一条树边。
相反,这条非树边与 不在上述简单路径中的树边 只能形成x个点x-1条边的树,删去任意一条边都会使这棵树不连通,而这棵树作为原最小生成树的一棵子树,这棵子树不连通的话原最小生成树一定也不连通。所以这条非树边不能代替任意一条非简单路径上的边。
如何快速处理树上的简单路径?树链剖分!
所以算法明确了:先预处理出最小生成树,然后将这棵最小生成树进行树链剖分,每一条边记录能够代替它的、权值最小的非树边的长度。对于每条非树边,利用树剖快速更新其两端点在树上的简单路径之间的所有边记录的最小值。查询时直接查询删除的边上存储的最小值即可。
实际代码可以将边的信息存在其儿子节点上,简化代码复杂度
有两种情况要特判Not connected:
原图不连通,对于所有询问都输出Not connected(树链剖分只是维护用其它边替换一条边的情况,如果原图不连通的话,不但生成树会建错,而且替换了边树也不连通);
原图连通,但删去这条边后没有边能替它连通两个块,此时树链剖分上询问这条边所得到的值应该是没更新过的初值,即inf。因此判断这个询问值如果是inf就输出Not connected即可。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #define inf 2147483647 6 #define N 50005 7 #define M 100005 8 using namespace std; 9 inline int read(){ 10 int x=0; bool f=1; char c=getchar(); 11 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 12 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 13 if(f) return x; 14 return 0-x; 15 } 16 int n,m,q; 17 struct inedge{ 18 int id,u,v,w; 19 bool operator <(const inedge &x)const{ 20 return w<x.w; 21 } 22 }in_e[M],pre_e[M]; 23 24 int head[M]; 25 struct edge{ 26 int v,w,next; 27 }e[N]; 28 inline int add(int i,int u,int v,int w){ 29 e[i].v=v, e[i].w=w, e[i].next=head[u], head[u]=i; 30 } 31 32 int seg[N<<2],tag[N<<2]; 33 int top[M],id[M],r_id[M],tot; //id是dfs序,r_id是dfs序号对应的节点编号 34 35 void pushdown(int o){ 36 if(tag[o]==inf) return; 37 seg[o<<1] = min(seg[o<<1], tag[o]); 38 seg[o<<1|1] = min(seg[o<<1|1], tag[o]); 39 tag[o<<1] = min(tag[o<<1], tag[o]); 40 tag[o<<1|1] = min(tag[o<<1|1], tag[o]); 41 tag[o]=inf; 42 } 43 44 void build(int l,int r,int o){ 45 seg[o]=tag[o]=inf; 46 if(l==r) return; //in_e[edge_p[r_id[l]]>>1].w 这sb错误 47 int mid=(l+r)>>1; 48 build(l,mid,o<<1), 49 build(mid+1,r,o<<1|1); 50 } 51 52 void update(int l,int r,int o,int left,int right,int val){ 53 54 if(l>=left && r<=right){ 55 seg[o]=min(seg[o],val); 56 tag[o]=min(tag[o],val); 57 return; 58 } 59 pushdown(o); 60 int mid=(l+r)>>1; 61 if(mid>=left) update(l,mid,o<<1,left,right,val); 62 if(mid<right) update(mid+1,r,o<<1|1,left,right,val); 63 } 64 65 int query(int l,int r,int o,int left,int right){ 66 if(l>=left && r<=right) return seg[o]; 67 pushdown(o); 68 int mid=(l+r)>>1, ret=inf; 69 if(mid>=left) ret = min(ret, query(l,mid,o<<1,left,right)); 70 if(mid<right) ret = min(ret, query(mid+1,r,o<<1|1,left,right)); 71 return ret; 72 } 73 74 int fa[M],size[M],dep[M],hson[M]; 75 void dfs1(int u,int f){ 76 fa[u]=f, size[u]=1; 77 for(int i=head[u];i;i=e[i].next){ 78 int v=e[i].v; 79 if(f!=v){ 80 dep[v]=dep[u]+1; 81 dfs1(v,u); 82 if(hson[u]==0 || size[hson[u]]<size[v]) hson[u]=v; 83 size[u]+=size[v]; 84 } 85 } 86 } 87 88 void dfs2(int u,int anc){ //anc表示重链链顶 89 top[u]=anc, id[u]=tot, r_id[tot++]=u; 90 if(hson[u]==0) return; 91 dfs2(hson[u],anc); 92 for(int i=head[u];i;i=e[i].next){ 93 int v=e[i].v; 94 if(v!=fa[u] && v!=hson[u]) dfs2(v,v); 95 } 96 } 97 98 void chain_update(int u,int v,int w){ 99 int tu=top[u],tv=top[v]; 100 while(tu!=tv){ 101 if(dep[tu]<dep[tv]) swap(tu,tv), swap(u,v); 102 update(1,n-1,1,id[tu],id[u],w); 103 u=fa[tu]; 104 tu=top[u]; 105 } 106 if(u==v) return; 107 if(dep[u]<dep[v]) swap(u,v); 108 update(1,n-1,1,id[hson[v]],id[u],w); 109 } 110 111 int chain_query(int u,int v){ 112 int tu=top[u],tv=top[v]; 113 if(tu!=tv){ //由于查询的是一条被断掉的边的两端点,因此这两点在原树上是相连的,只有当这条边是轻边的时候才会做这个 114 if(dep[tu]<dep[tv]) swap(tu,tv), swap(u,v); 115 return query(1,n-1,1,id[tu],id[u]); 116 } 117 else{ 118 if(dep[u]<dep[v]) swap(u,v); 119 return query(1,n-1,1,id[hson[v]],id[u]); 120 } 121 } 122 123 int bcj[N],cnt,sum; 124 bool istree[M],pre_istree[M]; 125 int find(int x){return x==bcj[x] ? x : bcj[x]=find(bcj[x]);} 126 bool merge(int x,int y){ 127 int fx=find(x),fy=find(y); 128 if(fx==fy) return 0; 129 bcj[fy]=fx; 130 return 1; 131 } 132 int main(){ 133 //freopen("faq.in","r",stdin); 134 //freopen("count.out","w",stdout); 135 n=read(),m=read(); 136 int i,u,v,w,Q,T,cx; 137 for(i=1;i<=m;i++) 138 in_e[i].id=i, in_e[i].u=pre_e[i].u=read(), in_e[i].v=pre_e[i].v=read(), in_e[i].w=pre_e[i].w=read(); 139 sort(in_e+1,in_e+m+1); 140 for(i=1;i<=n;i++) bcj[i]=i; //预处理并查集 141 for(i=1;i<=m;i++){ //最小生成树建出来,树链剖分用 142 if(merge(in_e[i].u, in_e[i].v)){ //两块未连通 143 add(i<<1 , in_e[i].u, in_e[i].v, in_e[i].w), 144 add(i<<1|1, in_e[i].v, in_e[i].u, in_e[i].w); 145 istree[i]=1, pre_istree[in_e[i].id]=1; 146 sum+=in_e[i].w; 147 if(++cnt==n-1) break; 148 } 149 } 150 151 if(cnt<n-1){ //整张图不连通 152 Q=read(); 153 for(i=0;i<Q;i++){T=read(); printf("Not connected\n");} 154 return 0; 155 } 156 157 dep[1]=1; 158 dfs1(1,0); //建树链 159 dfs2(1,1); //分轻重链 160 161 build(1,n-1,1); 162 for(i=1;i<=m;i++) 163 if(!istree[i]) chain_update(in_e[i].u, in_e[i].v, in_e[i].w); 164 165 Q=read(); 166 for(i=0;i<Q;i++){ 167 T=read(); 168 if(!pre_istree[T]) {printf("%d\n",sum); continue;} 169 int cx=chain_query(pre_e[T].u,pre_e[T].v); 170 if(cx==inf) printf("Not connected\n"); 171 else printf("%d\n",sum-pre_e[T].w+cx); 172 } 173 return 0; 174 }
嗯。。。





