【ARC072 E】Alice in linear land

被智商题劝退，告辞

题意

　　有一个人在一条数轴的距离原点为 \(D\) 的位置，他可以执行 \(n\) 次操作，每次操作为给定一个整数 \(d_i\)，这个人向原点的方向走 \(d_i\) 个单位，但如果走 \(d_i\) 个单位后他离原点的距离更远了，他就不会执行这个操作。
　　有 \(q\) 次询问，每次询问给定一个 \(y\)，询问能否将 \(d_y\) 修改为 \([0,\infty)\) 内的整数（注意可以改成 \(0\)），使得这个人执行 \(n\) 次操作后到不了原点。询问之间互相独立，即每次单点修改都是在原序列的基础上修改。
　　\(n\le 5\times 10^5\)
　　\(1\le d_i,D\le 10^9\)

题解

　　预处理出 \(y=1\cdots n\) 的答案。

　　考虑单点修改的实质：设 \(sum_i\) 表示执行完前 \(i-1\) 次操作后人的位置，询问是否存在一个到原点距离为 \(d_i\in [0,sum_{i-1}]\) 的整点，使得从该点出发进行第 \(i+1\) 到 \(n\) 次操作后这个人到不了终点。
　　因为本题的操作带条件，所以不能修改中间的某个操作。
　　但是我们可以预处理出 \(b_i\) 表示执行第 \(i\) 到 \(n\) 个操作后到达原点的最大出发位置（即到原点距离最远的位置）。
　　显然，答案是 yes 当且仅当 \(a_{y-1}\gt b_{y+1}\)（因为做一次操作只会使人到原点的距离变小或不变）。

　　那怎么预处理 \(b_i\) 呢？
　　构造一个函数 \(f(i)\) 表示人从距离原点为 \(i\) 的位置出发，执行一个参数为 \(k\) 的操作，到达距离原点 \(f(i)\) 的位置。
　　\(k\) 任取一个数 \(9\)，则把函数 \(f\) 打表

x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | \(\cdots\)
-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|
y | 1 | 2 | 3 | 4 | 4 | 3 | 2 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | \(\cdots\)

　　搬用官方题解的 \(x,y\) 图象（横轴是 \(x\)，纵轴是 \(y\)）
　　

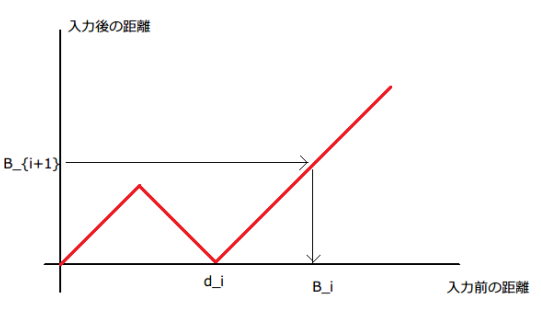
　　但我们可以通过修改 \(d_i\) 来得到 \([0,sum_{i-1}]\) 中的任意整数，所以我们把整个区间 \([0,i]\) 作为一个新函数 \(F\) 的自变量，\(F(i)\) 表示人从一个可能位于的区间 \([0,i]\) 出发，执行一个参数为 \(k\) 的操作，能到达的区间为 \([0,F(i)]\)。显然，\(F(i)\le i\)，即人可能位于的区间随着操作的增加而缩小。
　　这里写一下 \(F(i)\) 的等式：\(F(i)=\min(i,\max(i-k,\lfloor \frac{k}{2}\rfloor))\)
　　观察定义，还可以发现 \(F(i)\) 实际上就是 \(\max(f(j)\space |\space j\in [1,i])\)。
　　依然取 \(k\) 为 \(9\)，把函数 \(F\) 打表

x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | \(\cdots\)
-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|
y | 1 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | \(\cdots\)

　　因为 \(b_{n+1}=0\)，所以 \(b\) 数组可以倒推。现在我们考虑从某一个区间撤回一次操作所返回的区间。
　　设 \(F\) 的逆函数 \(G(i)\) 表示人从一个可能位于的区间 \([0,i]\) 撤回一个参数为 \(k\) 的操作，能到达的最大区间（因为我们要求 \(b_i\) 是合法的最大出发位置）。
　　观察函数 \(F\) 的表可得 $$G(i) = \begin{cases} i &(i\le \lfloor\frac{k}{2}\rfloor) \ i+k &(i\gt \lfloor\frac{k}{2}\rfloor) \end{cases}$$

　　于是倒推出 \(b\) 数组即可，根据 \(a_{y-1}\gt b_{y+1}\) 判断 yes / no 就行了。
　　复杂度 \(O(n)\)。

#include<bits/stdc++.h>
#define ll long long
#define N 500005
using namespace std;
inline ll read(){
	ll x=0; bool f=1; char c=getchar();
	for(;!isdigit(c); c=getchar()) if(c=='-') f=0;
	for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
	if(f) return x;
	return 0-x;
}
int n,q;
ll a[N+3],s[N+3],lim[N+3];
int main(){
	n=read(), s[0]=read();
	for(int i=1; i<=n; i++){
		a[i]=read();
		s[i]=min(abs(s[i-1]-a[i]),s[i-1]);
	}
	lim[n+1]=0;
	for(int i=n; i>=1; i--){
		if(lim[i+1]>=a[i]/2) lim[i]=lim[i+1]+a[i];
		else lim[i]=lim[i+1];
	}
	q=read(); int x;
	while(q--) x=read(), puts(lim[x+1]<s[x-1]?"YES":"NO");
	return 0;
}