【2018.10.4】CXM笔记(图论)
。1.给你一个无向图,问这张图的最小割是否唯一。输出yes或no。
跑一边最大流,那么最小割的那些正向边一定满流(也就是过不了了)。所以在残余网络上,从S到T和从T到S各广搜找一组最小割的边(即正向边满流),判断是否完全相同即可。
2.题意同上,求所有最小割的边集并和边集交。
做完最大流后,整张图的最小割的边就只有反向边了,所以残余网络只存在从T到S的路径而不存在从S到T的路径。
于是把满流的边和不在T到S的路径上的边都删掉,然后对剩下的边(正、反向边)组成的图缩点。
为什么要缩点?比如下面这个强连通分量(这里是简单的环):

很明显它们的正向边都还没满流,所以都不是割边,直接缩掉这样的SCC。
缩点后整张图变成了一个DAG。由于已经删掉了不在T到S的路径上的点,DAG的所有边都是最小割的边,其边集就是最小割的并。
最小割的交的求法类似T1。
3.一张有向图,从起点出发,中途有一条边会断掉,但你只有走到那条边的一端时才知道。问最坏情况下从起点到终点的最短路(任何一条边都可能断)。当然,你是以最优策略走的。点、边数<=2500,图可能有环。
首先,不可能不断边。
其次,如果有桥,那这个桥断了就是最坏情况,无解。
dp[i][j]表示从起点走到i,最坏情况下是编号为j的边断了,最短路是多少。
4.一张无向图,每种边权的边不会超过5个,求有多少种最小生成树。点、边数<=100000。
5.n个点,任意连边,问有多少种方案能使原图成为无向连通图。(poj1737 / bzoj3456)
(1) n<=8
(2) n<=12
(3) n<=100
(4) n<=2000
(5) n<=100000
6.n(<=2000)个节点的树,可以添加至多k(<=50)条边权为$W$的边,求在经过每条边的情况下从根节点出发回到根节点的最短路(加上的边也要经过)。
像这种图论题一般都要先推一些结论。
那这道题有什么结论呢?
我们可以先想想不加边的时候总路径是多少。当然,每条边都有去有回走了两次,因此此时最短路(当然只有一种路径)就是 所有边权之和*2。如图。

添加一条边(绿边)之后,经过所有边的路径大概就变成这样
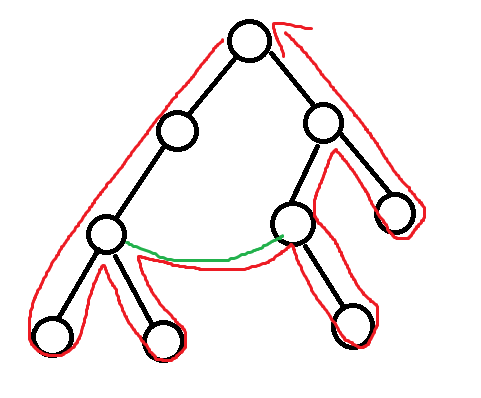
那到底少走了哪些路径呢?没错,如图的黄线部分可以只走一次。
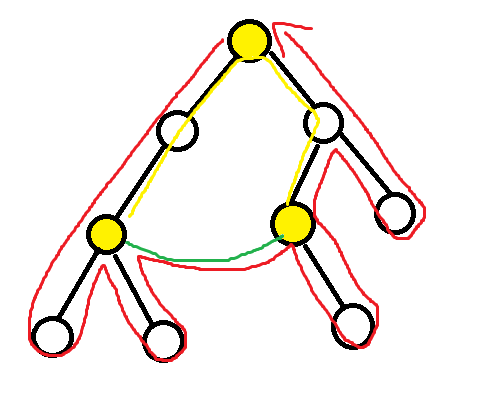
也就是说,黄线覆盖的边都是“有去无回”的。
当然不可能有无去无回的边,因为每条边至少经过一次(重要结论)
而黄线是哪一段?就是新连接的两点之间的原路径。也可以认为是两点到LCA的路径并。
让我们举出一个例图:

所以,每条边可以分走一次和走两次两种情况。我们可以考虑一条边的状况:
如果一条边经过两次(钦定这条蓝边),
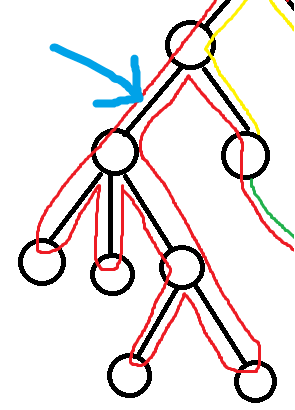
那它一定有偶数条儿子边有去无回(0也是偶数)。
为什么呢?
因为这条边要有去有回,那么 以这条边下端的点为根的子树 与其它子树(即除了这棵子树以外,原树的剩余部分)有偶数条加边。
如果连出去奇数条边的话,由于每条加边也都要走,所以最终一定会转出这棵子树而回不来了。如果出去后重走新边回来,那么可以证明出这棵子树的部分都是白走。因为要原路返回这条边,到其它子树走的那些边必定都是有来无回的,且最终多走了加边两次。可以证明这样不比不连奇数条边更优。
但是连出去偶数条边好像依然很复杂啊!这时每条边走的次数如下图。

我们发现,有两棵不同的子树的边都只走了一次,但是我们应该让一个点(比如上图的黄点)的dp限定在以这个点为根的子树中,而不影响其它子树,这样才能逐层向父亲合并答案。
好像dp不可做了,回去读题。
但再读题,我们注意到“所有加边的边权相等”,那这有一个什么性质呢?
...交叉边的情况好像可以忽略。
为什么可以这么想?
大家如果学过小学知识就能构思出这样一个交叉图(加边还是绿色):

它也可以这么连边到终点:

由于加边权值相等,且总是只经过一条黑边,所以两次路径长度相等。
换回这道题是个什么玩意:

我们发现两棵子树的边都只走了一次,那我们为什么要让它们交叉加边呢?这种情况等价于它们各自加边:
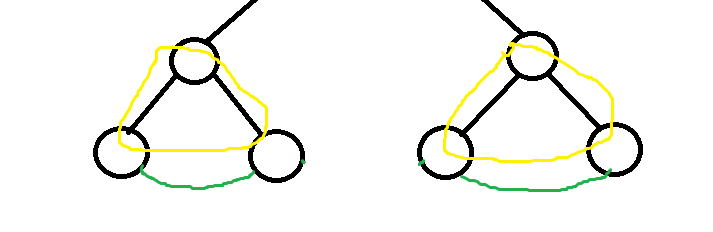
这样就可以只考虑以某个点为根的子树的情况了。
好了,我们解决了 以这条边下端的点为根的子树 向其它子树连出偶数条加边 这个棘手的问题,证明了连出去偶数条加边的情况等价于不连出去加边的情况。
所以,在我们的dp情况中,一条边(仍然是下图蓝边)要有去有回,那么 以这条边下端的点为根的子树 是独立的(即与其它子树没有加边)。
 (回到原图)
(回到原图)
前面说过,当一条边有去有回时,这条边有偶数条儿子边有去无回。
类似地,如果一条边只经过一次(有去无回),这条边有奇数条儿子边有去无回,这棵子树向其它子树连了奇数条加边。
根据前面对于前面那种情况下,加边数为偶数但只能是0 的证明,这里每2条与其它子树连的加边都可以消为在各自子树中连边,因此这棵子树与其它子树一定只连了1条加边。
然后可以推出,唯一的连向其它子树的加边 就在这条边(仍然是下图蓝边)的 一条有去无回的儿子边下的子树,这样就不用回到这条边了。

我们可以套用经典的树上背包转移:设 $dp(i,j,0/1)$ 表示在以点$i$为根的子树,该子树中加了$j$条边(也就是说加边的两端点都在该子树中才算!连到其它子树的不算),点$i$的父节点是否经过一次(经过两次记为0,经过一次记为1)。
再设$v$为当前扫到的$i$的一个儿子点,$w$为对应的儿子边,$k$为给以这个儿子为根的子树 分配的加边数,那就有四种转移。
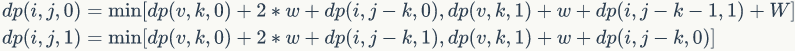
tips:$dp(i,j,0)$(根节点的父边有去有回)的转移中,$dp(v,k,1)+w+dp(i,j-k-1,1)+W$ 中 $j-k-1$ 一项的 $-1$ 意思是这个儿子是有去无回的,但要回到根节点,以这个儿子为根的子树 就要向整棵子树中已经转移过的部分连一条边,所以转移时独立出这条长度为$W$的加边。

最短路就是$\min[dp(root,x,0),dp(root,x,1)]$ | $0\leq x\leq k$。
时间复杂度$O(nk)$。
代码?不存在的,这只是个笔记





