【2018.10.2】Note of CXM
1.有一张无向图,现在要给每个点染上黑色或白色,最后每个点的染色代价是它与离这个点最近的不同色节点的距离。求最小代价。所有边权$\geq 0$且互不相同。
分三种情况:
两点都染了色:两点都跟其它点算过最小距离了,不用管。
一点染了色:相当于扩展连通块,染了色的点向没染色的点扩展染色,颜色相同。
两点都没染色:两点直接相连(且边长是最短距离)。
2.题目大意同上,求得到最小代价的方案数。
0的边两边的点有多少个子树,方案数就累加上2的多少次方。
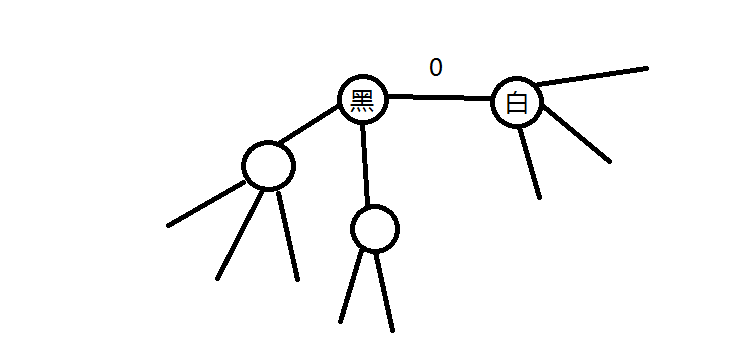
3.一张无向图,给每条边染两种颜色之一,使每个度大于等于2的点都连接两种颜色的边。问能否做到。Yes或No。
首先光秃秃的偶环(奇数条边)肯定无解(发芽就有解了),光秃秃的奇环(偶数条边)肯定有解(不知道这个结论的可以跳过这题了)。
环?想到了树。
可以先把这张图取出$n-1$条边,让整张图构成一棵树,
我们知道,树中只有三种边:树边(图中黑边)、回边(返祖边)(图中红边)、跨边(有向图特有)。
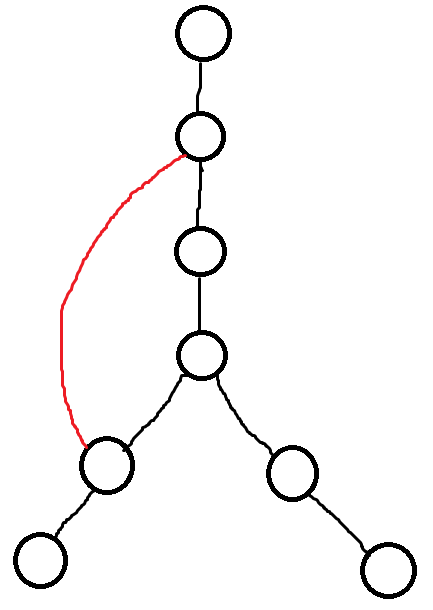
对于树上任意的度$\ge 2$ 的点,它的两边染上不同的颜色即可,如果再有一条返祖边连向它,这条新边染什么颜色都可以,必定能满足另一头的要求。
但对于度为 $1$ 的点呢?根和叶子结点都是度为1的点,这时候我们就要跑这个环。
只有这个环本身(即不算发芽)有偶数个点且发芽的情况需要我们考虑是否有解。
其实这就是偶环上发芽的情况。如图
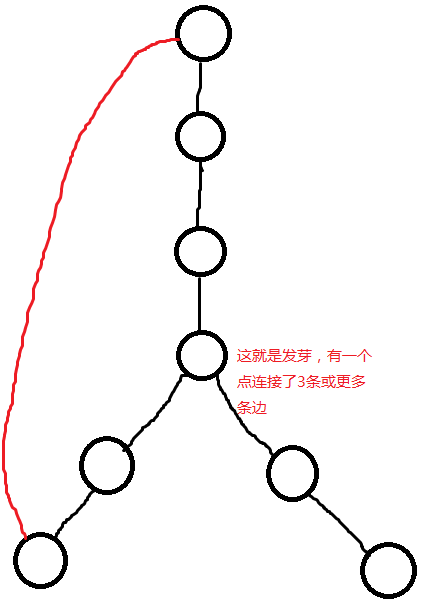
那么发芽点在原环上的两条相邻边就可以染成同色,然后把另一种颜色染到芽上。
但如果发的芽下面也有边连向了入读为1的边呢?
如果新连出来的环还是偶环,好像依然不可行。
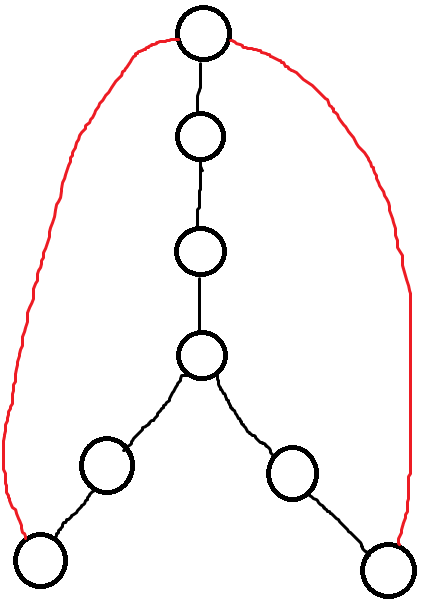
那什么情况下可行?如下。
只要偶环与奇环相套,至少就可以从发芽点把另一种颜色沿着芽流出去了。
结合这么一个知识:偶环套偶环=偶环
可得:只有整张图只要存在纯偶环(就是不与奇环相套的偶环)就无解,否则有解。
所以这是个结论题,以上都是推导,并非题解。
题解的话就再扯点没用的(找纯偶环的方法):去掉奇度点(它们是整张图的芽,处于被动染色状态,环上芽才是主动),把图的剩余部分做Tarjan求无向图强连通分量(MD准确地说是边双连通分量)。在每一个分量中任选一个起点,看是否存在经过偶数条边回到起点的方案。如果存在,说明存在奇环,这个强连通分量满足条件。如果所有的强连通分量都满足条件,说明图中不存在纯偶环,有解。否则存在纯偶环,无解。
4.有向图,边权只有0和1,求单源最短路。(线性算法)
我们都知道,广搜时总是取出队列中的第一个数。求最短路情况下,为了让更新尽量有意义,我们当然希望先从队列中取出(目前更新的)到起点距离尽量小的,这样可以尽量多地更新它周围点的最短路。
然后这题边权只有0和1,我们甚至不用写单调队列,如果按照上述贪心取法,我们发现广搜队列中 前面一段的距离值 与 后面一段的距离值 的差值不超过1。
为什么呢?
因为我们要取出到起点距离尽量小的,所以总是会取距离值相对较小的。并且更新时边权只会是0或1。
结合数学归纳法可知,
一开始队列中只有起点,距离为0,队列中距离值的差为0。
然后更新了周围的点,有些点的距离值更新为0,有些点的距离值更新为1。
然后我们一直更新 距离值为0的点 的周围的点,直到队列中所有点的距离值都为1。
此时已经不存在未被更新过的到起点距离为0的点了(广搜常识)。
此时队列中所有点的距离值是1。
然后把1当成之前的0,接下来更新出的距离值2当成之前的1,就归纳为一样的步骤了。
由此证明这样做的广搜队列中 前面一段的距离值 与 后面一段的距离值 的差值不超过1。
然后边权还只有0和1,队列操作比较简单,把通过权值为0更新的点接到队头,通过权值为1更新的点放到队尾即可。队头的点的距离值就是相对较小的。
拓展:有向图,边权只有0~20,求单源最短路。
把队列分割成21个桶,每个桶依次存$x,x+1,...,x+20$这21个距离值。广搜时不停取第一个桶中的点,把被该点更新距离的点 放到对应距离值的桶里。如果第一个桶中没有点,就把所有桶存放的距离值上调至使第一个桶中有点。
易证点肯定有桶放。
5.每个点有一个(开采矿物的)费用,边权依然只有0和1,求分别开采每个点的矿物时的最小费用。
6.执行k个操作,每个操作连接两个点,问每个操作后图中有多少条割边。(LCT会超时)
边双连通(环)的情况下给图缩点,这个图会变成一个森林。森林之间的每条边都是一条割边。因此用两个并查集维护,一个维护每个连通块的点,另一个维护每个边双连通块的点。





