【2018.8.10】四连测day4 题解
T1:给出一棵 $n$ 个节点的无根树,其中 $m$ 个节点是特殊节点,求对于任意 $i ∈ [0, m]$,包含 $i$ 个特殊节点的联通块个数$\mod 998244353$。 $1<=n,m<=1000$
输入格式
第一行包含两个正整数 $n,m$,表示树节点个数及特殊节点个数。
第二行包含 $m$ 个互不相同的正整数,表示所有特殊节点的编号。
接下来 $n$ 行,每行包含两个正整数 $u,v$,表示一条树边。
输出格式
输出包含 $m+1$ 个用空格隔开的整数,以此表示 $i=0,1,2,...,m$ 时,包含 $i$ 个特殊节点的联通块个数对 $998244353$ 取模的值。
树上连通块计数题,首先想到树形DP。
$f(i,j)$ 表示以点$i$为根的子树中,取$j$个关键点且必选根节点$i$的连通块的方案数。
那么可以发现,当考虑以$i$为根的子树的时候,我们只考虑不同子树之间合并的连通块,因为同一子树之间的连通块可以根据此原则,在子树内完成所有统计。
那具体怎么转移?又回到了子树乘法原理问题了……(不如说是树上背包)
$f(i,j) = \sum_{son_i} f(son_i,k) * f(i,j-k) | j<=size(i), k<=j$ //size(i)表示以i为根的子树中的特殊节点数量
这转移一看就知道怎么回事了
在这之前先特判一下根节点$i$是不是特殊节点,如果是的话就把$f(i,1)$初始化为1,否则把$f(i,0)$初始化为1。

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<vector> 5 #define MAXN 131072 6 #define MOD 998244353 7 using namespace std; 8 inline int read() 9 { 10 int x=0; bool f=1; char c=getchar(); 11 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 12 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 13 if(f) return x; 14 return 0-x; 15 } 16 int first[1024],nxt[2048],targ[2048],cnte=1; 17 bool special[1024]; 18 int ans[1024]; 19 int dp[1024][1024],cntd[1024]; 20 int poly[1024]; 21 void AddEdge(int u,int v) 22 { 23 targ[cnte]=v, nxt[cnte]=first[u], first[u]=cnte++, swap(u,v); 24 targ[cnte]=v, nxt[cnte]=first[u], first[u]=cnte++; 25 } 26 void DP(int x,int Fa) 27 { 28 if(special[x]) dp[x][1]=1, cntd[x]=2; 29 else dp[x][0]=1, cntd[x]=1; 30 for(int i=first[x];i;i=nxt[i]) 31 { 32 if(targ[i]==Fa) continue; 33 int y=targ[i]; 34 DP(y,x); 35 for(int i=0;i<cntd[x]+cntd[y]-1;i++) poly[i]=0; 36 for(int i=0;i<cntd[x];i++) 37 for(int j=0;j<cntd[y];j++) 38 (poly[i+j] += (long long)dp[x][i]*dp[y][j]%MOD) %= MOD; 39 cntd[x] += cntd[y]-1; 40 for(int i=0;i<cntd[x];i++) dp[x][i]=poly[i]; 41 } 42 for(int i=0;i<cntd[x];i++) (ans[i]+=dp[x][i])%=MOD; 43 (++dp[x][0])%=MOD; //一个点都不选的情况也要算上(一开始只特判了选非特殊节点的根节点) 44 } 45 int main() 46 { 47 freopen("tree.in","r",stdin); 48 freopen("tree.out","w",stdout); 49 int n=read(),m=read(); 50 for(int i=0;i<m;i++) special[read()]=1; 51 for(int i=1;i<n;i++) AddEdge(read(),read()); 52 DP(1,0); 53 for(int i=0;i<=m;i++) printf("%d%c",ans[i],i==m?'\n':' '); 54 return 0; 55 }
时间复杂度根据均摊原则可知近似$O(nm)$
2018.10.1 update:这里证明了一下复杂度
T2:有 $n$ 个机器人和 $m$ 个配件,每个机器人需要若干个的配件。每个机器人对每个配件都有一定适配度,但都可互相搭配。现在请你求出,给每个机器人分配其所需数量的配件,所有机器人对其分配到的配件的适配度之和最大是多少?
输入格式
第一行包含两个正整数 $n,m$,依次表示机器人和配件个数。
第二行包含 $n$ 个正整数 $a_i$,依次表示从 $1$ 到 $n$ 号机器人所需配件数,保证 所需配件总数 $\leq m$。
接下来是一个 $n$ 行 $m$ 列的正整数矩阵 $C$,其中第 $i$ 行第 $j$ 列的数值表示,$i$ 号机器人对 $j$ 号配件的适配度。
输出格式
输出一个整数,表示答案。
$1<=n<=100, 1<=m<=200$
适配度最大值$S \leq 10^7$
不穿衣服的费用流裸题。

如此建图,从源点S到$i$号机器人连上流量为$a_i$、费用为$0$的边,从$i$号机器人到$j$号配件连上流量为$1$、费用为$C(i,j)$的边,从$i$号配件到汇点T连上流量为$1$,费用为$0$的边。这么建刚好限定了每个机器人选择配件的数量、每个配件只能被选一次,那么最大费用就是答案(注意我们平常写的是最小费用最大流!)
注意不要写EK,会被卡时成40分。

1 #include<queue> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<algorithm> 7 #define inf 0x7f7f7f7f 8 #define maxn 201 9 #define maxm 401 10 #define S n+m+1 11 #define T n+m+2 12 using namespace std; 13 inline int read(){ 14 int x=0,f=1; char c=getchar(); 15 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 16 for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0'; 17 return x*f; 18 } 19 class Dinic_Enhancer 20 { 21 private: 22 struct edge{ 23 int v,w,x,next; //w表示流量,x表示费用 24 }e[maxm<<1]; 25 int cnt,head[maxn]; 26 int depth[maxn],cur[maxn];//cur就是记录当前点u循环到了哪一条边(弧优化) 27 int dis[maxn],fa[maxn],faedge[maxn]; 28 bool inq[maxn]; 29 public: 30 int n,m; 31 void init() 32 { 33 cnt=0; 34 memset(head,-1,sizeof(head)); 35 36 n=read(),m=read(); 37 for(int i=1;i<=n;i++){ 38 add_edge(S,i,read(),0); 39 } 40 for(int i=1;i<=n;i++) 41 for(int j=1;j<=m;j++) add_edge(i,n+j,1,read()); 42 43 for(int i=n+1;i<=n+m;i++) add_edge(i,T,1,0); 44 } 45 void add(int u,int v,int w,int x) 46 { 47 e[cnt].v=v; 48 e[cnt].w=w; 49 e[cnt].x=x; 50 e[cnt].next=head[u]; 51 head[u]=cnt++; 52 } 53 void add_edge(int u,int v,int w,int x) 54 { 55 add(u,v,w,x); 56 add(v,u,0,-x); 57 } 58 bool spfa() 59 { 60 queue<int> Q; 61 memset(depth,0,sizeof(depth)); 62 fill(dis+1,dis+T+1,-inf); 63 memset(inq,0,sizeof inq); 64 depth[S]=1; 65 dis[S]=0; 66 Q.push(S); 67 int i,u; 68 while(!Q.empty()) 69 { 70 u=Q.front(); Q.pop(); 71 inq[u]=0; 72 for(i=head[u];i!=-1;i=e[i].next) 73 if(dis[e[i].v]<dis[u]+e[i].x && e[i].w>0) 74 { 75 dis[e[i].v]=dis[u]+e[i].x; 76 depth[e[i].v]=depth[u]+1; 77 fa[e[i].v]=u, faedge[e[i].v]=i; 78 if(!inq[e[i].v]){ 79 inq[e[i].v]=1; 80 Q.push(e[i].v); 81 } 82 } 83 } 84 if(dis[T]==-inf) return 0; 85 return 1; 86 } 87 int dinic() 88 { 89 int ans=0,i,flow; 90 while(spfa()) 91 { 92 int u=T,flow=inf; 93 while(u!=S) flow=min(flow,e[faedge[u]].w), u=fa[u]; 94 u=T; 95 while(u!=S) e[faedge[u]].w-=flow, e[faedge[u]^1].w+=flow, u=fa[u]; 96 ans+=dis[T]; 97 } 98 return ans; 99 } 100 }de; 101 102 int main(){ 103 de.init(); 104 printf("%d\n",de.dinic()); 105 return 0; 106 }

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<queue> 5 #define MAXN 606 6 #define MAXM 40040 7 using namespace std; 8 inline int read() 9 { 10 int x=0,t=1,c; 11 while(!isdigit(c=getchar()))if(c=='-')t=-1; 12 while(isdigit(c))x=x*10+c-'0',c=getchar(); 13 return x*t; 14 } 15 struct ZKW 16 { 17 int first[MAXN],targ[MAXM<<1],nxt[MAXM<<1],flow[MAXM<<1],cost[MAXM<<1],cnte=2; 18 int dist[MAXN],s,t,inf,ans=0; 19 bool inq[MAXN],vis[MAXN]; 20 void AddEdge(int u,int v,int l,int c) 21 { 22 targ[cnte]=v;flow[cnte]=l;cost[cnte]=c;nxt[cnte]=first[u];first[u]=cnte++;swap(u,v); 23 targ[cnte]=v;flow[cnte]=0;cost[cnte]=-c;nxt[cnte]=first[u];first[u]=cnte++; 24 } 25 bool SPFA() 26 { 27 memset(dist,127,sizeof dist); 28 memset(&inf,127,sizeof(int)); 29 memset(inq,0,sizeof inq); 30 queue<int> Q; 31 dist[t]=0; 32 inq[t]=1; 33 Q.push(t); 34 while(!Q.empty()) 35 { 36 int x=Q.front();Q.pop();inq[x]=0; 37 for(int i=first[x];i;i=nxt[i]) 38 { 39 if(flow[i^1]&&dist[targ[i]]>dist[x]-cost[i]) 40 { 41 dist[targ[i]]=dist[x]-cost[i]; 42 if(!inq[targ[i]]) 43 { 44 Q.push(targ[i]); 45 inq[targ[i]]=1; 46 } 47 } 48 } 49 } 50 return dist[s]!=inf; 51 } 52 int DFS(int x,int maxflow) 53 { 54 if(x==t||!maxflow){ans+=dist[s]*maxflow;return maxflow;} 55 if(vis[x])return 0; 56 vis[x]=1; 57 int ret=0,f; 58 for(int i=first[x];i&&maxflow;i=nxt[i]) 59 { 60 if(dist[targ[i]]==dist[x]-cost[i]) 61 { 62 if(f=DFS(targ[i],min(maxflow,flow[i]))) 63 { 64 ret+=f; 65 flow[i]-=f; 66 flow[i^1]+=f; 67 maxflow-=f; 68 } 69 } 70 } 71 vis[x]=0; 72 return ret; 73 } 74 int solve(int source,int tank) 75 { 76 s=source;t=tank;int Flow=0; 77 while(SPFA()) 78 { 79 Flow+=DFS(s,2147483647); 80 } 81 return Flow; 82 } 83 }zkw; 84 int n,m; 85 int main() 86 { 87 freopen("robot.in","r",stdin); 88 freopen("robot.out","w",stdout); 89 n=read();m=read(); 90 for(int i=1;i<=n;i++)zkw.AddEdge(i+1,1,read(),0); 91 for(int i=1;i<=n;i++) 92 for(int j=1;j<=m;j++) 93 zkw.AddEdge(n+1+j,i+1,1,-read()); 94 for(int j=1;j<=m;j++) 95 zkw.AddEdge(0,n+1+j,1,0); 96 zkw.solve(0,1); 97 printf("%d",-zkw.ans); 98 return 0; 99 }
T3:有一维空间内 $n$ 个点,编号从 $1$ 到 $n$,编号为 $i$ 的点坐标为 $x_i$。现在,请选出编号连续的一些点,使得被选出的所有点到某一点的距离和的最小值不超过一正整数 $m$,问最多能选出多少点?
输入格式
第一行,包含两个正整数 $n,m$,依次表示点数和距离和限制。
第二行,包含 $n$ 个正整数 $x_i$,依次表示每个点的坐标。
输出格式
输出共一行,表示最多选取点数。
$1<=n<=10^5, 1<=m<=10^9, 1<=x_i<=10^6$
难度堪比提高组D2T3
第一眼看到这题,不会,于是想想暴力做法。
首先我们得知道这样一个幼儿园知识:n个数中,与这n个数的差的绝对值(在空间意义里就是距离)之和最小的数 是这n个数的中位数。
为什么?简单证明:
把这n个数从小到大排序。假设我们先认为与这n个数的差的绝对值(在空间意义里就是距离)之和(下面都称之为答案)是最小的数(第一个数),我们把答案改为第二个数,则从第1个数到第2个数的距离会增加$dis(1,2)$,第2~n个数到第2个数的距离都会减少$dis(1,2)$,那么很明显距离减少的比增加的多,距离总和也会减少。把答案从第二个数改为第三个数,再改为第四个数……一直改到中位数为止,距离减少的都比增加的多(距离减少的占一半以上),所以距离总和不断减少;而从中位数改到比中位数大的下一位时,距离增加的数就超过一半了,而距离减少的数随之少于一半,且之后距离增加的数会越来越多,这时距离总和就会不断增加。
总结一下,就是 总距离随数的排名的变化 的图像是单峰下凸的,且排名在最中间(中位数)时所有数到它的总距离最小。大家可以手动写个数列验证一下。
下面回到正题:
用两重循环枚举所有选点区间(按编号顺序),搜一遍区间里的点找出中间点(可以理解为n个坐标的中位数)并暴力求解所有被选点到它的总距离就可以了。
这样的复杂度是$O(n^3)$,可以过40%的数据。
我们很快发现最外层的两重循环枚举区间可以优化。这样想:一个选点区间的所有数到该区间中位数的距离总和不超过$m$的话,那更短的区间到其中位数的距离总和一定也能不超过$m$(至少把满足条件的选点区间中去掉头或尾一个点的情况就可以,总距离只会减少那个点到中位数的距离,不会增加,因此依然可以不超过$m$)。因此区间答案随区间长度单调递减,把其中一重枚举区间长度的循环改为二分即可。
这样的复杂度是$O(n^2 \log n)$。
到了这里简单的优化已经不能影响复杂度了,因此开始考虑数据结构。你很惊奇地发现$x_i \leq 10^6$,坐标值这么小肯定可以入手啊!结合数轴的背景,我们可以用值域线段树(权值线段树)/平衡树优化辣!
$10^6$大小的值域线段树的做法就是先把开头区间的坐标值都插进去,之后每次移动选点区间其实只会删去开头的坐标值,并插入结尾后的一个新坐标值,这样分析的话每个坐标值最多只会被插入一次和删去一次,插入的复杂度可控制在$O(n \log x_i)$内。然后对于每个区间,在当时的权值线段树中跑一边树,从根遍历到中位数所在叶子节点即可,每次找中位数的复杂度可控制在$O(\log x_i)$里。
然而找出了中位数好像还得暴力求每个点到这个中位数的距离啊?!
你又惊奇地发现,其实每个点到中位数的距离之和相当于如图的橙色线条长度之和
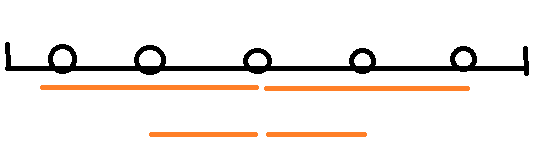
它相当于 坐标轴总长 减去 中位数前每个坐标到坐标轴起点的距离(坐标值)的和 再减去 中位数后每个坐标到坐标轴终点的距离的和。
借助上面那个值域线段树,维护每个区间内所有数 到坐标轴起点的距离之和 以及 到坐标轴终点的距离之和 即可。然后通过上述计算得到当前选点区间内所有坐标到中位数的距离。
加上外层套的二分区间长度,这样的复杂度是$O(n \log n \log x_i)$。
丧心病狂的出题人为了卡$log^2$的常数,临考试结束的时候临时取消了这题的氧气优化,然而这个复杂度好像还是能卡过
正解是$O(n \log x_i)$的。其实最后这步优化很简单,把二分区间长度套枚举起点 改为滑动窗口即可。根据上述区间答案随区间长度单调递减这个推论,从第一个点开始,当滑动窗口右端点右移到不满足条件(区间内的被选点到中位数的距离和超过 $m$)时,右移左端点缩小区间即可。滑动窗口枚举区间的复杂度是$O(n)$的,答案就是窗口长度的最大值。)
这是值域线段树做法,如果把值域线段树改成平衡树也可以维护这些,树可以只开$n$位,但是平衡树常数大,容易被卡成狗……

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #define MAXN 1048576 5 using namespace std; 6 inline long long read() 7 { 8 long long x=0,t=1;int c; 9 while(!isdigit(c=getchar()))if(c=='-')t=-1; 10 while(isdigit(c))x=x*10+c-'0',c=getchar(); 11 return x*t; 12 } 13 int n; 14 long long m; 15 int x[MAXN]; 16 int size[1048576<<2]; 17 long long sumv[1048576<<2]; 18 void maintain(int o,int L,int R) 19 { 20 int m=L+R>>1,lc=o<<1,rc=lc|1; 21 size[o]=size[lc]+size[rc]; 22 sumv[o]=sumv[lc]+sumv[rc]; 23 } 24 void Add(int o,int L,int R,const int pos,const int v) 25 { 26 if(L==R) 27 { 28 size[o]+=v; 29 sumv[o]=(long long)size[o]*L; 30 } 31 else 32 { 33 int m=L+R>>1,lc=o<<1,rc=lc|1; 34 if(pos<=m)Add(lc,L,m,pos,v); 35 else Add(rc,m+1,R,pos,v); 36 maintain(o,L,R); 37 } 38 } 39 int GetKthPos(int o,int L,int R,const int k) 40 { 41 if(L==R) 42 { 43 return L; 44 } 45 else 46 { 47 int m=L+R>>1,lc=o<<1,rc=lc|1; 48 if(size[lc]>=k)return GetKthPos(lc,L,m,k); 49 else return GetKthPos(rc,m+1,R,k-size[lc]); 50 } 51 } 52 long long toLeft(int o,int L,int R,const int ql,const int qr) 53 { 54 if(ql<=L&&R<=qr) 55 { 56 return sumv[o]-(long long)size[o]*ql; 57 } 58 else 59 { 60 int m=L+R>>1,lc=o<<1,rc=lc|1; 61 long long size=0; 62 if(ql<=m)size+=toLeft(lc,L,m,ql,qr); 63 if(m<qr)size+=toLeft(rc,m+1,R,ql,qr); 64 return size; 65 } 66 } 67 long long toRight(int o,int L,int R,const int ql,const int qr) 68 { 69 if(ql<=L&&R<=qr) 70 { 71 return (long long)size[o]*qr-sumv[o]; 72 } 73 else 74 { 75 int m=L+R>>1,lc=o<<1,rc=lc|1; 76 long long size=0; 77 if(ql<=m)size+=toRight(lc,L,m,ql,qr); 78 if(m<qr)size+=toRight(rc,m+1,R,ql,qr); 79 return size; 80 } 81 } 82 long long CountPrice(int size) 83 { 84 int mid=GetKthPos(1,1,1000000,(size+1)>>1); 85 long long ret=0; 86 ret+=toRight(1,1,1000000,1,mid); 87 ret+=toLeft(1,1,1000000,mid,1000000); 88 return ret; 89 } 90 int main() 91 { 92 freopen("choose.in","r",stdin); 93 freopen("choose.out","w",stdout); 94 n=read();m=read(); 95 for(int i=1;i<=n;i++)x[i]=read(); 96 int L=1,R=0,ans=0; 97 for(R=1;R<=n;R++) 98 { 99 Add(1,1,1000000,x[R],1); 100 while(CountPrice(R-L+1)>m) 101 Add(1,1,1000000,x[L++],-1); 102 ans=max(ans,R-L+1); 103 } 104 printf("%d",ans); 105 return 0; 106 }
总而言之,题出的不错,就是题面写错数据卡常低分罚跑圈应该吐槽吐槽




