【安徽集训】空洞

Description

　　你有一个空心的 \(n\) 维超矩形，第 \(i\) 维坐标在 \([0,r_i]\) 内。现在你把矩形内所有满足 \(\sum\limits_{i=1}^n x_i\le S\) 的位置全部填满了液体，求液体的体积对 \(998244353\) 取模（如果是个分数就求逆元）。
　　subtask3：对于\(1\le i\le n\) 有 \(r_i=S\)
　　subtask4：\(1\le n,r_i\le 500,\space S\le 10^9\)

Solution

　　先手玩 subtask3 的特殊情况（不用考虑坐标范围限制）
　　二维情况下，答案就是红色区域面积，显然是 \(\frac{1}{2}\)
　　
　　三维情况下，答案就是绿色线条与前右下角三条邻边围成的空间体积，根据小学知识可知是 \(\frac{1}{6}\)（可以用微积分证明）
　　
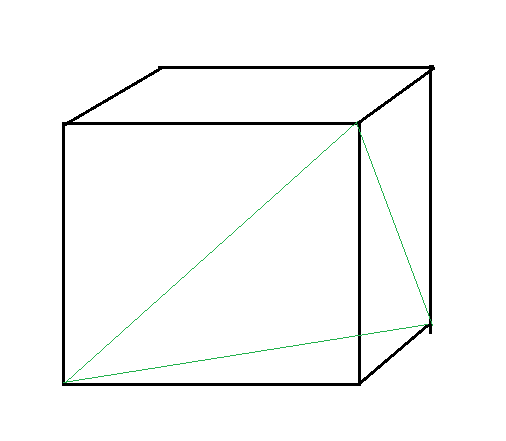
　　所以可以猜测答案就是 \(\frac{S^n}{n!}\)。
　　那对于所有 \(r_i\le S\) 的情况，答案会不会就是 \(\frac{\prod_{i=1}^n r_i}{n!}\)？确实是的，可以用微积分证明……

　　然后考虑朴素情况。
　　像这种多重限制的问题，一般不容易直接求解，我们尝试求坐标不在范围内的情况数，然后从总方案数中减掉。
　　举个例子，\(n=2,\space r_1=1,\space r_2=4,\space S=2\)
　　我们钦定第 \(1\) 维坐标不满足条件，即 \(x_1\gt 1\)
　　我们发现一组方程 $$\begin{cases} x_1+x_2\le 2 \ x_1\gt 1 \end{cases}$$ 可以上下同时 \(-1\) 得到 $$\begin{cases} x_1+x_2\le 1 \ x_1\gt 0 \end{cases}$$
　　我们本来就有 \(x_i\ge 0\)，而在实数内随机意义下，随机到一个确定实数的概率可以认为是 \(0\)，故等价于我们本来就有 \(x_i\gt 0\)，即下面那个式子可以扔了。
　　然后问题又变成了求解上面那个式子，由于没有了坐标范围限制，直接用上一个 subtask 的结论解就行了……

　　容斥出的答案就是 $ans = \sum\limits_S (-1)^{|S|} (S-\sum\limits_{i=1}^n r_i)