【基本操作】树上启发式合并の详解

树上启发式合并是某些神仙题目的常见操作。

这里有一个讲得详细一点的，不过为了深刻记忆，我还是再给自己讲一遍吧！

 

DSU（Disjoint Set Union），别看英文名挺高级，其实它就是并查集……

DSU on tree，也就是树上的启发式合并（众所周知，并查集最重要的优化就是启发式合并）。

然后咱们来考虑一个基础题：给出一棵树，每个节点有颜色，询问一些子树中不同的颜色数量（颜色可重复）。祖传数据（$100000$）。

当然，这道题可以被各种方法切，比如带修莫队（做法自行百度）。

但莫队的时空复杂度是 $O(n\times \sqrt{n})$ 的，稍微差点。

又比如这里讲的主席树。

但主席树的空间复杂度是 $O(n\times log^2(n))$（虽然时间复杂度还是 $O(n\times log(n))$），我们考虑换一个严格 $O(n\times log(n))$ 的做法。

没错，就是树上启发式合并。

考虑一个问题，就是这道题为什么不能朴素地直接用一个数组把子树的每种颜色数量返回？

因为对于一个点，以它儿子为根的各个子树之间的答案是没有联系的，我们的遍历一定是有一个顺序的，那后遍历的子树就去不掉先遍历的子树的答案影响。

 

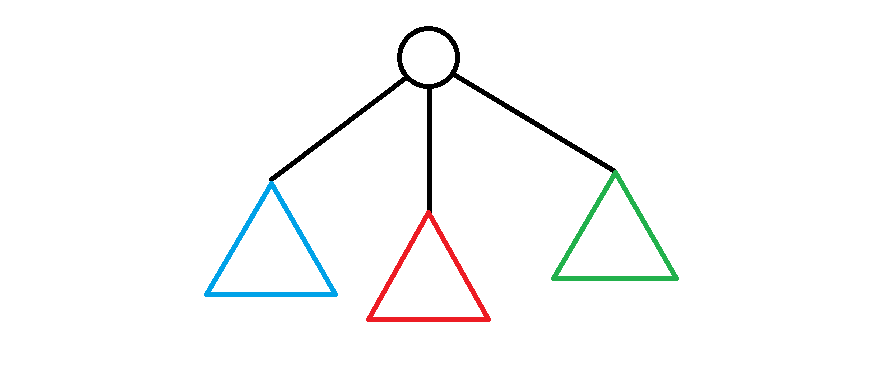
比如这三个同层的子树，假如你先遍历了蓝色子树，之后你进入红色子树时，由于你要保留蓝色子树的答案（它得返回给祖先），你只能在暴力减掉蓝色子树的答案，这样时间复杂度就退化了。 

那怎么存下所有答案，并完成各个儿子子树内的所有询问呢？

Use your 复杂度分析知识

我们可以像树链剖分一样，找出每个点的重儿子（即点数最多的那个儿子子树对应的儿子），然后我们考虑一些睿智的优化。

我们先遍历其它的所有儿子（它们都是轻儿子），依次完成它们各自的子树内的所有询问，然后我们就头铁地修改，即进入子树时该更新哪种颜色的数量 就更新哪种颜色的数量，退出这棵子树时暴力减掉子树内的所有答案（即各个颜色在这棵子树内的变化量），再遍历其它子树。

简单地说，第一次遍历所有轻儿子，解决它们子树内的询问，然后出来时减掉影响。

最后我们再遍历重儿子，同样处理子树内的询问，但出来时保留里面统计的答案，并把其它轻儿子对应子树的所有点的颜色都重新统计上。这样就可以得到整棵子树的答案， 并返回它了。

 

这看起来就是暴力优化啊！！除了换了一下遍历儿子的顺序，省了一次消影响（重儿子的影响不用减了），好像与暴力没其它区别了！！

但这个优化就让整个时间复杂度降到了严格 $O(n\times log(n))$，而且可以如下证明：

我们考虑以一个点 $x$，以它的一个轻儿子为根的子树，这棵子树的点数 必定小于或等于 以点 $x$ 为根的子树的 $\frac{1}{2}$（大于 $\frac{1}{2}$ 它就必定是重儿子了）。虽然一个点会有很多轻儿子，轻儿子们的点数和可能大于 以点 $x$ 为根的子树的 $\frac{1}{2}$，但我们无法确定与它有影响关系的 树的深度，也就无法从这个角度证明。

可以反过来想，一个轻儿子为根的、大小为 $size$ 子树，通过上述条件可知它一定至少会被合并到一棵大小为 $2\times size$ 的子树（换一种方式说，就是从整棵树的根节点到树中任意一点的路径上最多有 $log(n)$ 条轻边，这是树链剖分的基础），每次合并都要额外（即不算遍历整棵树所必须的那一次）遍历统计 $2$ 次子树（循环减掉子树答案、循环加上子树答案），为常数复杂度，所以每个轻儿子最多会被合并 $log(n)$ 次，总时间复杂度最多是 $O(n\times log(n))$ 级别。

那去掉整棵数中的所有轻儿子，剩下的就是一些重儿子了。重儿子为根的子树的合并复杂度是多少呢？

每个重儿子只会被合并一次（它们都在重链上，且重链上每个点被加入答案后就不会被去掉了），所以合并它们的总复杂度最多是 $O(n)$ 级别。

 

最后遍历整棵树的 $O(n)$ 及 处理所有询问的 $O(m)$ 的固定复杂度与上述操作是同层的，所以总时间复杂度是 $O(n\times log(n))$ 级别的。