C++实现离散余弦变换（参数为Eigen矩阵）

C++实现离散余弦变换（参数为Eigen矩阵）

问题描述

昨天写了一个参数为二维指针为参数的离散余弦变换，虽然改进了参数为二维数组时，当数组大小不确定时声明函数时带来的困难，但使用指针作为参数也存在一些不足之处，比如需要手动寻址、容易出现指针越界等。因此这篇文章中的代码对昨天的代码做了进一步的改进，将函数的参数设置为Eigen矩阵，很好的避免了上述问题。

DCT

代码的主体跟之前的代码没啥差别，主要就是改变了函数的参数类型

// DCT - Discrete Cosine Transform
void DCT( MatrixXd &input, MatrixXd &output )
{
    cout<<"Test in DCT"<<endl;
    double ALPHA, BETA;
    int u = 0;
    int v = 0;
    int i = 0;
    int j = 0;

    int row = input.rows();
    int col = input.cols();

    for(u = 0; u < row; u++)
    {
        for(v = 0; v < col; v++)
        {
            if(u == 0)
            {
                ALPHA = sqrt(1.0 / row);
            }
            else
            {
                ALPHA = sqrt(2.0 / row);
            }

            if(v == 0)
            {
                BETA = sqrt(1.0 / col);
            }
            else
            {
                BETA = sqrt(2.0 / col);
            }

            double tmp = 0.0;
            for(i = 0; i < row; i++)
            {
                for(j = 0; j < col; j++)
                {
                    tmp += input(i,j) * cos((2*i+1)*u*PI/(2.0 * row)) * cos((2*j+1)*v*PI/(2.0 * col));
                }
            }
            output(u,v) = ALPHA * BETA * tmp;
        }
    }

    cout << "The result of DCT:" << endl;
    for(int m  = 0; m < row; m++)
    {
        for(int n= 0; n < col; n++)
        {
            cout <<setw(8)<< output(m,n) <<" \t";
        }
        cout << endl;
    }
}

注意比较上述Eigen数组的访问方法。访问Eigen矩阵的i行j列元素是，使用的是（i，j）

IDCT代码

// Inverse DCT
void IDCT( MatrixXd &input, MatrixXd &output )
{
    cout<<"Test in IDCT"<<endl;
    double ALPHA, BETA;
    int u = 0;
    int v = 0;
    int i = 0;
    int j = 0;

    int row = input.rows();
    int col = input.cols();

    for(i = 0; i < row; i++)
    {
        for( j = 0; j < col; j++)
        {
            double tmp = 0.0;
            for(u = 0; u < row; u++)
            {
                for(v = 0; v < col; v++)
                {
                    if(u == 0)
                    {
                        ALPHA = sqrt(1.0 / row);
                    }
                    else
                    {
                        ALPHA = sqrt(2.0 / row);
                    }
                    if(v == 0)
                    {
                        BETA = sqrt(1.0 / col);
                    }
                    else
                    {
                        BETA = sqrt(2.0 / col);
                    }
                    tmp += ALPHA * BETA * input(u,v)* cos((2*i+1)*u*PI/(2.0 * row)) * cos((2*j+1)*v*PI/(2.0 * col));
                }
            }
            output(i,j)= tmp;
        }
    }

    cout << "The result of IDCT:" << endl;
    for(int m  = 0; m < row; m++)
    {
        for(int n= 0; n < col; n++)
        {
            cout <<setw(8)<< output(m,n)<<"\t";
        }
        cout << endl;
    }
}

测试代码

#include <iostream>
#include <math.h>
#include<cstdio>
#include <iomanip>
#include<algorithm>
#include<fstream>
#include<math.h>
#include<string>
#include <Eigen/Dense> 

using namespace std;
using namespace Eigen;

#define PI 3.1415926
int main()
{
    int i = 0;
    int j = 0;
    int u = 0;
    int v = 0;

    const int rows = 4;
    const int cols = 2 ;

    double inputdata[rows][cols] = {
        {89,23},
        {73,48},
        {45,67},
        {56, 102},
    };

    double outputdata[rows][cols];

    MatrixXd minput;
    MatrixXd moutput;

    minput.setZero(4,2);
    moutput.setZero(4,2);

    for (int i = 0; i < minput.rows(); i++)
    {
        for (int j = 0; j < minput.cols(); j++)
        {
            minput(i,j) = inputdata[i][j];
        }
    }

    DCT( minput, moutput );
    IDCT(moutput, minput);

    system("pause");
    return 0;
}

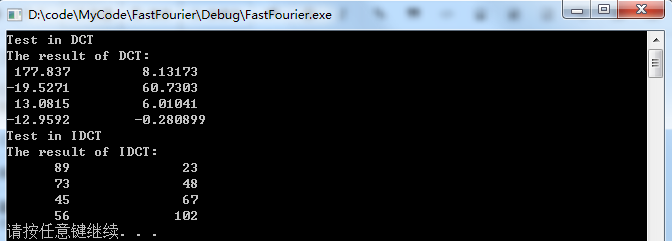
运行结果

 

转载请注明出处：http://www.cnblogs.com/scut-linmaojiang/p/5016811.html