C++实现离散余弦变换（参数为二维指针）

C++实现离散余弦变换（参数为二维指针）

写在前面

到目前为止已经阅读了相当一部分的网格水印等方面的论文了，但是论文的实现进度还没有更上，这个月准备挑选一些较为经典的论文，将其中的算法实现。在实现论文的过程中，发现论文中有用到一些空域转频率域的算法。因此也就想到了实现一下离散余弦变换。虽然本文的代码和网上很多已有的代码很类似，思路都没有太多的差别，但是本文有一个比较重要的改进。具体的说，网上现有DCT算法输入的是一个固定的二维数组。当二维数组作为函数参数进行传递时，至少需要给出第二个维度的大小，否则编译器会报错。但是在图形图像处理中，当我们希望使用DCT变换把某个图形或者图像转换到频域时，可能我在调用DCT函数之前事先并不知道图形或者图像的规模，因此这种传参方式较大限制了代码的使用。本文的一个改进就是，DCT函数的参数不再是二维数组，而是传入一个二维指针，通过手动寻址来实现函数功能。

离散余弦变换理论基础

我想大家比较熟知的是傅立叶变换。其实离散余弦变换跟傅立叶变换差不多。二维离散余弦变换的定义由下式表示：

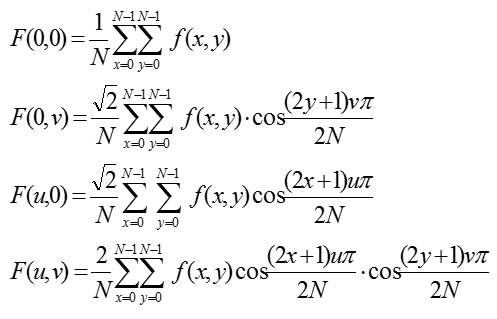
反变换表示如下：

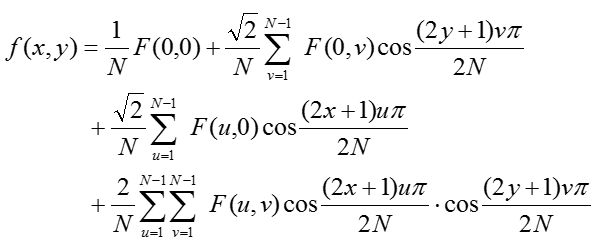
代码实现

根据上面的公式，很容易就能写出代码

// DCT - Discrete Cosine Transform
void DCT( double ** input, double ** output, int row, int col )
{
    cout<<"Test in DCT"<<endl;
    double ALPHA, BETA;
    int u = 0;
    int v = 0;
    int i = 0;
    int j = 0;

    for(u = 0; u < row; u++)
    {
        for(v = 0; v < col; v++)
        {
            if(u == 0)
            {
                ALPHA = sqrt(1.0 / row);
            }
            else
            {
                ALPHA = sqrt(2.0 / row);
            }

            if(v == 0)
            {
                BETA = sqrt(1.0 / col);
            }
            else
            {
                BETA = sqrt(2.0 / col);
            }

            double tmp = 0.0;
            for(i = 0; i < row; i++)
            {
                for(j = 0; j < col; j++)
                {
                    tmp += *((double*) input + col*i + j ) * cos((2*i+1)*u*PI/(2.0 * row)) * cos((2*j+1)*v*PI/(2.0 * col));
                }
            }
            *((double*) output + col*u + v) = ALPHA * BETA * tmp;
        }
    }

    cout << "The result of DCT:" << endl;
    for(int m  = 0; m < row; m++)
    {
        for(int n= 0; n < col; n++)
        {
            cout <<setw(8)<< *((double*) output + col*m + n)<<" \t";
        }
        cout << endl;
    }
}

注意代码中的函数参数不是二维数组，而是一个指向二维数组的指针。相应的反变换的代码如下：

// Inverse DCT
void IDCT( double ** input, double ** output, int row, int col )
{
    cout<<"Test in IDCT"<<endl;
    double ALPHA, BETA;
    int u = 0;
    int v = 0;
    int i = 0;
    int j = 0;

    for(i = 0; i < row; i++)
    {
        for( j = 0; j < col; j++)
        {
            double tmp = 0.0;
            for(u = 0; u < row; u++)
            {
                for(v = 0; v < col; v++)
                {
                    if(u == 0)
                    {
                        ALPHA = sqrt(1.0 / row);
                    }
                    else
                    {
                        ALPHA = sqrt(2.0 / row);
                    }
                    if(v == 0)
                    {
                        BETA = sqrt(1.0 / col);
                    }
                    else
                    {
                        BETA = sqrt(2.0 / col);
                    }
                    tmp += ALPHA * BETA * *((double*) input + col*u + v )* cos((2*i+1)*u*PI/(2.0 * row)) * cos((2*j+1)*v*PI/(2.0 * col));
                }
            }
            *((double*) output + col*i + j) = tmp;
        }
    }

    cout << "The result of IDCT:" << endl;
    for(int m  = 0; m < row; m++)
    {
        for(int n= 0; n < col; n++)
        {
            cout <<setw(8)<< *((double*) output + col*m + n)<<"\t";
        }
        cout << endl;
    }
}

测试代码

#include <iostream>
#include <math.h>
#include<cstdio>
#include <iomanip>
#include<algorithm>

using namespace std;
#define PI 3.1415926
int main()
{
    int i = 0;
    int j = 0;
    int u = 0;
    int v = 0;

    const int rows = 3;
    const int cols = 3;

    double inputdata[rows][cols] = {
        {89,101,114},
        {97,115,131},
        {114,134,159},
    };

    double outputdata[rows][cols];

    DCT( (double**)inputdata, (double**)outputdata,rows, cols )；
    IDCT( (double**)outputdata, (double**)inputdata,rows,cols );

    system("pause");
    return 0;
}

程序运行结果如下：

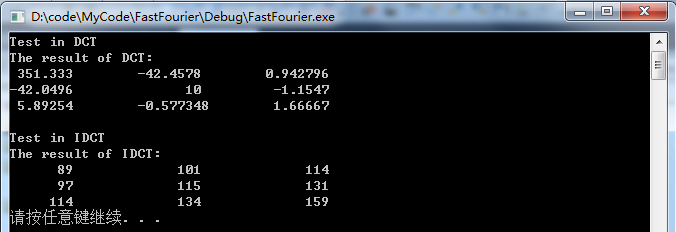
小结

之后可以对代码进行升级，不再使用二维数组作为参数传递，而是使用Eigen类型作为参数，这样代码更加清晰，并且内存管理等方面也更加方便。

 

转载请注明出处：http://www.cnblogs.com/scut-linmaojiang/p/5013590.html