非均衡分类问题的思考与问题与解决思路
前言
在前面的文章中,讨论了一些分类算法。然后,有一点一直忽视了,就是非均衡的分类问题。
分均衡分类有两种情形
情形一:正例和反例数量相差非常大。
比如,分析信用卡信息集里面的正常样本和诈骗样本。正常样本固然比诈骗样本要多的多了。
情形二:分类正确/错误的代价不同。
比如,分析病人的体检数据,我们肯定是希望不漏过任何一个病例。因此,有病诊断为无病的后果要比无病诊断为有病的后果严重的多。
这样的非均衡分类的情形导致了仅仅是使用分类错误率还分析分类质量是不科学的。
本文就将介绍一些新的衡量分类质量的参数,工具。基于这些,可以对分类代码进行优化,以得到更符合实际用途的分类器。
工具一:混淆矩阵 (confusion matrix)
首先介绍几个概念:
1. TP: 真阳。就是实际为真 预测为真。
2. FN: 假阳。就是实际为真 预测为假。
3. FP: 假阴。就是实际为假 预测为真。
4. TN: 真阴。就是实际为假 预测为假。
列出这几个参数的详细表格(矩阵格式)即为混淆矩阵,如下图所示:
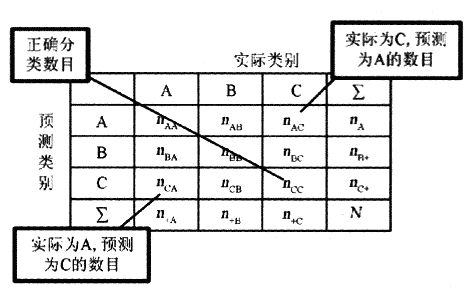
这样的表格能够很好的帮助人们进行分类的质量评估。然而,对于程序,或者说机器来说,需要的是一个基于代价的硬性指标。
因此,下面这个工具 - ROC曲线才是机器学习中处理非均衡分类问题的利器。
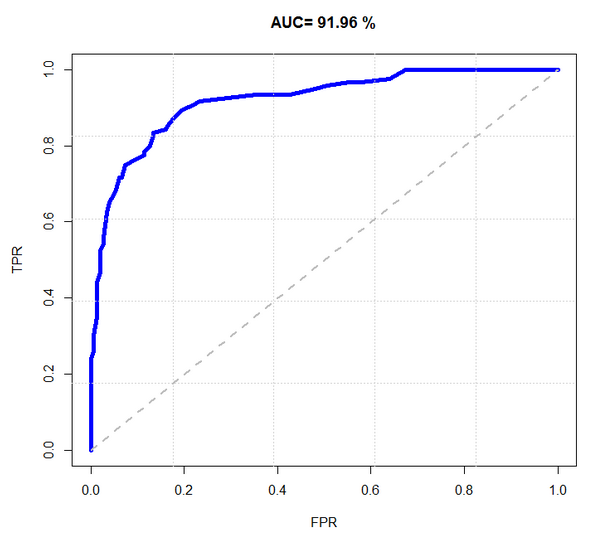
工具二:ROC 曲线
ROC 曲线图就是一个平面的二维图。横轴为假阳率;纵轴为真阳率。
真阳率 = TP / TP+FN。就是实际为真,预测也为真的样本在所有预测为真的样本中的概率。
假阳率 = FP / FP+FN。就是实际为假,预测为真的样本在所有预测为假的样本中的概率。
而移动的方向是按照阈值变化而变化的。每个点代表了一个阈值的真阳率和假阳率。
如下图所示例:
 m
m
对于 ROC 模型,图中蓝色线段与横轴的面积占总面积的比率 - AUC 可以衡量整个分类的性能,但是切记它不能代替对整个线段以及错误率的观察。
AUC理论最佳值是1。如果说 "真” 这一类的权重更重要(好比诊断出病人有病),那么AUC应该在0.5 - 1之间才好,而且是越接近1越好。
绘制 ROC 曲线
绘制 ROC 曲线首先必须要获取到分类器结果的预测强度,基于预测强度才能够调整真阳率,假阳率。
如下代码是 ROC 统计图的绘制代码,可将其进行封装,以在需要时随时调用。
1 #========================================== 2 # 输入: 3 # predStrengths: 预测强度 4 # classLabels: 分类结果 5 # 输出: 6 # 该分类器的ROC统计图 7 #========================================== 8 def plotROC(predStrengths, classLabels): 9 '绘制分类器的ROC统计图' 10 11 import matplotlib.pyplot as plt 12 # 当前绘制节点 13 cur = (1.0,1.0) 14 # AUC 统计 15 ySum = 0.0 16 # 实际为真的分类数 17 numPosClas = sum(numpy.array(classLabels)==1.0) 18 # x轴移动步长 19 yStep = 1/float(numPosClas); 20 # y轴移动步长 21 xStep = 1/float(len(classLabels)-numPosClas) 22 # 预测强度排序(下标排序) 23 sortedIndicies = predStrengths.argsort() 24 # 设置画布 25 fig = plt.figure() 26 fig.clf() 27 ax = plt.subplot(111) 28 29 # 以预测强度递减的次序绘制ROC统计图像 30 for index in sortedIndicies.tolist()[0]: 31 if classLabels[index] == 1.0: 32 delX = 0; delY = yStep; 33 else: 34 delX = xStep; delY = 0; 35 ySum += cur[1] 36 37 ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b') 38 cur = (cur[0]-delX,cur[1]-delY) 39 40 ax.plot([0,1],[0,1],'b--') 41 plt.xlabel('False positive rate'); plt.ylabel('True positive rate') 42 plt.title('ROC curve for AdaBoost horse colic detection system') 43 ax.axis([0,1,0,1]) 44 plt.show() 45 print "the Area Under the Curve is: ",ySum*xStep
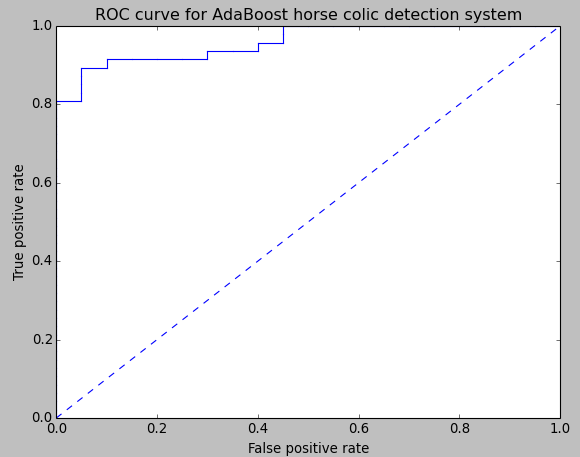
采用上函数对上一篇文章中的 AdaBoost 分类器(10次迭代)绘制 ROC 统计直方图的结果如下(数据集格式和以前一样,内容都是随机生成的。):
其他一些度量方案
1. 可设立代价函数,计算混淆矩阵的代价值(所有成员乘以对应权重然后求和)。
2. 对于那种样本数量不均衡的问题(如信用卡诈骗这类),可以调整样本数量。比如5000和真样本,50个假样本,那么就从这5000个真样本里只随机选择50个真样本。
小结
关于分类算法的讨论,先告一段落了。
以后可能会有对其中某些算法的进一步分析的学习文章分享,但现在我的目光将从分类转移到监督学习中的下一个主题 - 回归。
元旦第二天假期也快结束了,新的一年要加把劲,好好学习的同时多多注意锻炼身体,迎接充满挑战的未来。


