电力电子技术学习笔记
电力电子技术学习笔记
更新于2018-11-30
整流电路
单相桥式不控整流
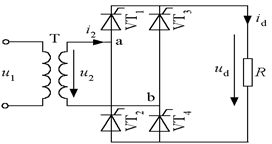
- VT2和VT3将负半周期的正弦波变成正电压加在负载两端
- 直流电压Ud，一个周期脉动两次
- 环流/换相点：器件切换状态，对应正弦电压的过零点
- 二极管为不控器件，其通断由所加电压决定，器件自然切换通断，因此其换向点叫自然换相/流点
- 任何一个晶闸管电路，所有晶闸管换成二极管时的环流/换相点即为自然换流/相点
单相桥式全控整流
-
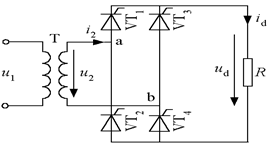
共同点：一个正弦周期内，变压器二次侧电流正、负两个半周期电流方向相反且波形对称，因此平均值为0，即直流分量为0，不存在直流磁化问题，直流磁化影响变压器的利用率。
-
整流期间，负载两端的电压反向、电流方向均不变；但二次侧电压、电流方向一直是周期变化的，就是有正有负，方向改变，所以不存在直流分量。而单半控整流电路，只有一个晶闸管，非桥式，不能起到变换电流方向作用，因此变压器二次侧会存在脉动且电流方向恒定的直流分量，造成直流磁化。
-
一组串联晶闸管导通时，另一组晶闸管为截止状态
-
改变触发延迟角\(\alpha\)即可改变整流输出电压大小\(U_d\)，这种方式叫做相控
-
移相范围：改变\(\alpha\)使整流输出电压平均值从最大值降到最小值的变化范围。
-
晶闸管承受电压的问题
- 当一组晶闸管截止，另一组晶闸管的触发脉冲没到之前，两组晶闸管全部截止。负载电压、电流均为0，电阻看成导线，两组晶振管，每组串联后并联在二次侧，晶闸管等效成阻抗元件，故每个晶振管此时承受的电压为\(1/2U_d\)，即此刻晶闸管承受的正反向电压中，正向电压即为最大正向电压、
- 串联导通时，导通组每个晶闸管承受电压为0；截止组必然承受反向电压，且承受最大反向电压为$ \sqrt{2}U_rms$
-
电阻负载下，负载两端的电压电流保持保持波形同步，为周期变化且不含有反压的正弦b半波的一部分，脉动的馒头波；变压器二次侧电压和电流同步，电压周期变化正负均有的正弦波；电流周期变化正负均有的正弦波的一部分
触发角和导通角的关系：\(\theta=\pi-\alpha\)
参数计算
- 积分范围：a-PI
-
整流输出电压平均值
电流积分除以周期
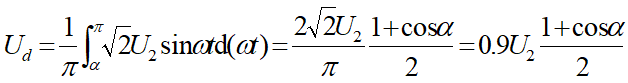
根据\(\alpha\)判断移相范围为0-180
-
整流输出电流平均值
根据电压平均值去算
-
整流输出电流有效值
电流平方积分除以周期再开根号
-
每个晶闸管平均电流
因晶闸管轮流导通，所以为输出平均电流的一半；本质上就是一半的积分值
-
每个晶闸管有效值
关健搞清楚输出的波形
因晶闸管轮流导通，所以为输出电流有效值的\(1/\sqrt2\)倍，因为一半的积分值需要开方才是有效值
-
变压器二次侧电流
正负均有，和二次侧电压波形同步
阻感负载
- 在一组晶闸管截止，且另一组晶闸管的触发脉冲尚未到来时，因电感储能，电流在自然换向点处不断续，实现续流，原本应该截止（全部截止）并且承受一半反压的晶闸管组此刻在绪流二极管的作用下未关断（仍导通），二次侧过零点后的反向电压仍能加到负载上，因此负载上出现反压。
- 一旦另一组晶闸管导通，原本导通的晶闸管组因立刻承受最大反向反压儿截止。
- 阻感负载下，负载两端的电压电流波形类型不同，电压为周期变化且含有反压的正弦波的一部分；电流因大电感存在变成平直的直流。变压器的二次侧电压为正负均有的正弦波；电流为正负均有的平直的直流。这里的直流方向会周期变化，只不过大小平直，其实还是交流，因此不会造成变压器直流磁化。
- 周期仍然可以PI去积分，积分范围 a-PI+a
- 移相范围看计算结果
参数计算
-
移相范围
-
整流输出电压平均值
积分
-
整流输出电流平均值
除法
-
整流输出电流有效值
输出直流，有效值等于平均值
-
晶闸管电流平均值
整流输出电流平均值的一半
-
晶闸管电路有效值
整流输出电流有效值\(1/\sqrt2\)倍
-
二次侧电流波形
大电感情况下，为平直的正负均有的直流矩形波
