[转] 连连看连通算法

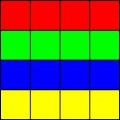
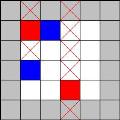
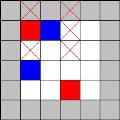
连连看算法

【原帖地址】

为了方便，我们假设棋盘大小为 4 * 4，棋子有 4 种。

数字化和布局算法

　　首先，我们知道每种棋子有 4 个，我们可以先按顺序把每种棋子排好，然后再随机取其中两个棋子交换一下，多次交换后，棋子就是乱的了。参考下面两图，图中用 4 种颜色表示 4 种棋子：

(1)初始排布		(2)多次随机交换两个棋子后

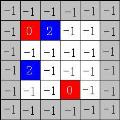
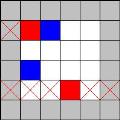
　　实际上程序内部是不需要认识棋子的图象的，只需要用一个 ID 来表示，界面上画出来的棋子图形是根据 ID 取资源里的图片画的。比如上图中用 4 种颜色表示 4 种棋子，我们可以定义红色棋子的 ID 为 0，绿色为 1，蓝色为 2，黄色为 3。另外，如果棋子被消除 ID 可以定义为 -1。把 ID 放在一个二维矩阵，画到界面上时，根据距阵里元素的位置和值(ID)决定在什么位置画什么颜色棋子。

　　我见过两种风格的连连看，有一种是和我写的水晶连连看一样，连线可以伸到棋子矩行外面，比如图(2)中的第一行有两个红色棋子，这两个是可以连的；另外一种和 QQGame 里的连连看一样，连线不能伸到棋子矩行外面，也就是说图(2)中的第一行的两个红色棋子是不能连的。程序内部棋子都是数字，这两种风格的差别在于 ID 距阵的大小，第一种是：(行数 + 2) * (列数 + 2)；第二种是：行数 * 列数，这更简单，所以下面只说第一种。

　　(行数 + 2) * (列数 + 2) 的距阵，边界上都是 -1（也可以定义为别的，比如 -2），即留了空位给连线通过，而且这些空位不能安排任何棋子，在有些“关”的时候，棋子会移动，也不可以移动到边界的空位上！参考图(3)，其中灰色表示边界空位，灰色边界内部是棋盘：

(3)棋盘矩阵化		(4)棋子数字化

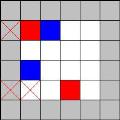
连通算法

　　（1）直连型：太简单不说了。

　　（2）一折型：其实相当于两个棋子划出一个矩形，这两个棋子是一对对角顶点，另外两个顶点如果可以同时和这两个棋子直连，那就说明可以“一折连通”。见图(5)两个红色棋子的连通情况，右上角打叉的位置就是折点。

(5)一折型示例

　　（3）二连型：这个是重点，其实用人眼来观察很简单的，就是有些人没意识到规律，虽然网络上有很多代码，但是比较难看懂，所以我才写了本文。见图(6)两个红色棋子的连通情况：

(6)二折型示例

　　判断是否是二连型的算法需要做两个方向上的扫描：水平扫描和垂直扫描。先看水平的，首先，要找到棋子往左右可以延伸的范围，这里的延伸是指左右有多少空的位置；然后，计算水平坐标上两个棋子延伸出来的公共部分；最后，找公共的水平坐标里有没有可以“垂直直连”的。用图(7)(8)(9)说明：

(7)棋盘矩阵化		(8)水平延伸		(9)求得水平延伸公共范围

　　从图(9)可以看出，左边缘（第零列）有一对叉可以直连，所以红色棋子是可以“二折连通”的！接着再看垂直扫描：

(10)棋盘矩阵化		(11)垂直延伸		(12)求得垂直延伸公共范围

　　从图(12)可以看出，上边缘（第零行）有一对叉可以直连，第二行也有一对，所以红色棋子是可以“二折连通”的！

　　仔细一想，其实这个算法也适合“直连型”和“一折型”的，它们都是“二折型”的特例。