新手立体四子棋AI教程(3)——极值搜索与Alpha-Beta剪枝
上一篇我们讲了评估函数,这一篇我们来讲讲立体四子棋的搜索函数。
一、极值搜索
极值搜索是game playing领域里非常经典的算法,它使用深度优先搜索(因为限制最大层数,所以也可以称为迭代加深搜索)来遍历未来n步的走子情况。在每层模拟中都会选择对自己最优的位置,通过最大化自己的利益(也就是上一篇提到的评估算法)来取胜。α-β剪枝也是类似的思想,只不过效率更高,因为它删减了一些不需要遍历的结点。
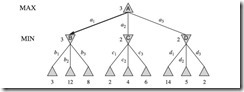
下图是一个极小极大算法的例子,MAX层代表自己,总是选取下面三个结点中的最大值,MIN层代表对手,总是选取下面一层结点中的最小值。在此例子中,MAX下一步会选择a1。
Minimax的伪代码如下(递归实现):
function minimax(node, depth) // 指定当前节点和搜索深度 // 如果能得到确定的结果或者深度为零,使用评估函数返回局面得分 if node is a terminal node or depth = 0 return the heuristic value of node // 如果轮到对手走棋,是极小节点,选择一个得分最小的走法 if the adversary is to play at node let α := +∞ foreach child of node α := min(α, minimax(child, depth-1)) // 如果轮到我们走棋,是极大节点,选择一个得分最大的走法 else {we are to play at node} let α := -∞ foreach child of node α := max(α, minimax(child, depth-1)) return α;
二、实现
首先我们声明可能会用到的函数:
int dfs(int board[4][4][4], int deep = 6); int findWhiteScoreMaxValue(int board[4][4][4],int deep); int findWhiteScoreMinValue(int board[4][4][4],int deep);
dfs函数是我们函数对外调用的接口,也是DFS搜索的启动函数。接下来的搜索为了避免混乱,我们都将白方考虑为自己。
findWhiteScoreMaxValue(board, deep);
在dfs函数中中我们通过上述语句开始搜索。
int ChessBoard::findWhiteScoreMaxValue(int board[4][4][4], int deep) {if(deep <= 0)
{
int score = getSideScore(board, chessPicesStatus::white) - getSideScore(board, chessPicesStatus::black);
return score;
} else {
int maxVal = -1000000; PicesPosList list = getAvailablePos(board,chessPicesStatus::white); for(auto iter = list.begin();iter != list.end();iter++) { board[iter->x][iter->y][iter->z] = chessPicesStatus::white; int val = findWhiteScoreMinValue(board, deep -1); if(val > maxVal) { maxVal = val; whiteTargetPos.x = iter->x; whiteTargetPos.y = iter->y; whiteTargetPos.z = iter->z; } board[iter->x][iter->y][iter->z] = chessPicesStatus::empty; } return maxVal; } }
在上述代码中,我们首先判断是不是叶子节点,如果是则直接返回当前的结果,如果不是,开始下一步迭代。
在迭代中,我们用第一篇介绍过的方法,产生当前所有可能的落子位置,然后在每个位置下棋,进入Min层(对手走子)的搜索,在当前节点所有可能性搜索完毕后,判断当前节点是否是最大节点,如果是则保存当前最大值以及走子位置,如果不是则继续搜索下一个位置。Min层与Max大部分代码一致,此处不再贴出。
三、Alpha-Beta剪枝算法
在大部分棋类AI中,剪枝是必须的。假设我们计算未来六步的结果,也就是六层的迭代,每层都有16中可能性,那么节点数量将达到16^6=16,777,216个,耗时极大,实际上最好一步能控制在 5 秒 以内。顺便说一下层数的问题,首先思考层数必须是偶数。因为奇数节点是AI,偶数节点是玩家,如果AI下一个子不考虑玩家防守一下,那么这个估分明显是有问题的。然后,至少需要进行4层思考,如果连4四层都考虑不到,那就是只看眼前利益,那么棋力会非常非常弱。 如果能进行6层思考基本可以达到随便赢普通玩家的水平了。
Alpha Beta 剪枝算法的基本依据是:棋手不会做出对自己不利的选择。依据这个前提,如果一个节点明显是不利于自己的节点,那么就可以直接剪掉这个节点。
前面讲到过,AI会在MAX层选择最大节点,而玩家会在MIN层选择最小节点。那么如下两种情况就是分别对双方不利的选择:
- 在MAX层,假设当前层已经搜索到一个最大值 X, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比X还小的值,那么就直接剪掉此节点。
解释一下,也就是在MAX层的时候会把当前层已经搜索到的最大值X存起来,如果下一个节点的下一层会产生一个比X还小的值Y,那么之前说过玩家总是会选择最小值的。也就是说这个节点玩家的分数不会超过Y,那么这个节点显然没有必要进行计算了。
通俗点来讲就是,AI发现这一步是对玩家更有利的,那么当然不会走这一步。
- 在MIN层,假设当前层已经搜索到一个最小值 Y, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比Y还大的值,那么就直接剪掉此节点。
这个是一样的道理,如果玩家走了一步棋发现其实对AI更有利,玩家必定不会走这一步。
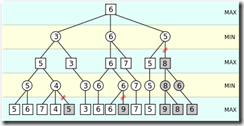
如上图所示,在第二层,也就是MIN层,当计算到第三个节点的时候,已知前面有一个3和一个6,也就是最小值为3。 在计算第三个节点的时候,发现它的第一个孩子的结果是5,因为它的孩子是MAX节点,而MAX节点是会选择最大值的,那么此节点的值不会比5小,因此此节点的后序孩子就没有必要计算了,因为这个节点不可能小于5,而同一层已经有一个值为3的节点了。
其实这个图里面第三层分数为7的节点也是不需要计算的。
这是 MAX 节点的剪枝,MIN节点的剪枝也是同样的道理,就不再讲了。 Alpha Beta 剪枝的 Alpha 和 Beta 分别指的是MAX 和 MIN节点。
我们直接上代码:
int ChessBoard::findWhiteScoreMaxValue(int board[4][4][4], int deep,int alpha,int beta) { if(deep <= 0) { int score = getSideScore(board, chessPicesStatus::white) - getSideScore(board, chessPicesStatus::black); return score; } else { int maxVal = -1000000; PicesPosList list = getAvailablePos(board,chessPicesStatus::white); for(auto iter = list.begin();iter != list.end();iter++) { board[iter->x][iter->y][iter->z] = chessPicesStatus::white; int val = findWhiteScoreMinValue(board, deep -1,alpha,maxVal > beta ? maxVal : beta); if(val > maxVal) { maxVal = val; whiteTargetPos.x = iter->x; whiteTargetPos.y = iter->y; whiteTargetPos.z = iter->z; } board[iter->x][iter->y][iter->z] = chessPicesStatus::empty; if(maxVal > alpha) break; } return maxVal; } } int ChessBoard::findWhiteScoreMinValue(int board[4][4][4], int deep,int alpha,int beta) { if(deep <= 0) { int score = getSideScore(board, chessPicesStatus::white) - getSideScore(board, chessPicesStatus::black); return score; } else { int minVal = 1000000; PicesPosList list = getAvailablePos(board,chessPicesStatus::black); for(auto iter = list.begin();iter != list.end();iter++) { board[iter->x][iter->y][iter->z] = chessPicesStatus::black; int val = findWhiteScoreMaxValue(board, deep -1, minVal < alpha ? minVal : alpha ,beta); if(val < minVal) { minVal = val; blackTargetPos.x = iter->x; blackTargetPos.y = iter->y; blackTargetPos.z = iter->z; } board[iter->x][iter->y][iter->z] = chessPicesStatus::empty; if(val < beta) break; } return minVal; } }
至此,我们的搜索函数已经基本完成。但是此时的剪枝效率非常低,因为剪枝的效率依赖于大小排列是否整齐。比如在Max层,最理想的效果一定是各个节点从大到小排列,Min层也是一样的道理。所以在下一篇文章中我会讲到到启发式搜索。
参考文献:
https://www.cnblogs.com/pangxiaodong/archive/2011/05/26/2058864.html
https://www.zhihu.com/question/27221568/answer/127599152
http://blog.csdn.net/lihongxun945/article/details/50668253
致谢!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号