新手立体四子棋AI教程(2)——价值评估函数

上一篇我们完成了整个程序的基础框架，那么在讲到真正的搜索算法前，我们先来看看五子棋如何评估当前局势，以及如何计算某个位置的价值。

 

一、五子棋

在五子棋中，包括成五，活三，活二等定势，下图为山东师范大学董红安在2005年的硕士毕业论文中使用的的评分表，可以供我们来参考。

 

但是对于四子棋来说，上述评分却并不适用，因为棋盘空间大小的原因，任何一个维度只有4子的空间，一旦没有落成，或是任意一个位置被对方下了，那么该位置将没有任何价值。

 

二、潜在可能性评估

 

 

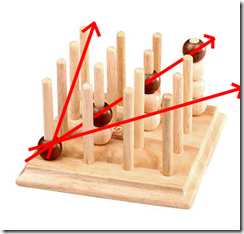
我们以这张图来举例，当黑棋在(0,3,0)这个位置落子后，我们来分析之后的可能性。

首先在xy平面内，有如下三种方式取胜：

 

除xy平面内之外，我们还需要考虑立体斜着四子连成的情况：

 

 

最后还要考虑垂直四子连成的情况：

 

并且在计算价值时，我们要注意，在上述任何一种情况中，只要预计的路线上有对方棋子出现，那么这条线（仅仅是单条线，不是整体）的评分将为0，因为他已经不能实现胜利。

 

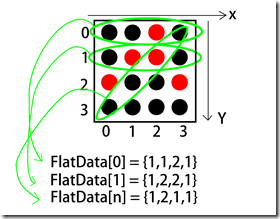
三、展平化

为了更方便的计算，我们通过将chessBoard[x][y][z]符合规则的任意连续的四个子编入序列，并通过计数的方式实现计分。

我们通过一段代码来了解这个过程：

struct flatData{
    int a;
    int b;
    int c;
    int d;
};

typedef std::vector<flatData> PicesFlatDataList;

int isWin(int board[4][4][4]);

int ChessBoard::isWin(int board[4][4][4])
{
    PicesFlatDataList flats;

    for(int y = 0;y < 4;y++)
    {
        for(int z = 0;z < 4;z++)
        {
            flatData data;
            data.a = board[0][y][z];
            data.b = board[1][y][z];
            data.c = board[2][y][z];
            data.d = board[3][y][z];
            flats.push_back(data);
        }
    }

    for(int x = 0;x < 4;x++)
    {
        for(int z = 0;z < 4;z++)
        {
            flatData data;
            data.a = board[x][0][z];
            data.b = board[x][1][z];
            data.c = board[x][2][z];
            data.d = board[x][3][z];
            flats.push_back(data);
        }
    }

    for(int x = 0;x < 4;x++)
    {
        for(int y = 0;y < 4;y++)
        {
            flatData data;
            data.a = board[x][y][0];
            data.b = board[x][y][1];
            data.c = board[x][y][2];
            data.d = board[x][y][3];
            flats.push_back(data);
        }
    }

    for(int y = 0;y < 4;y++)
    {
        flatData data;
        data.a = board[0][y][0];
        data.b = board[1][y][1];
        data.c = board[2][y][2];
        data.d = board[3][y][3];
        flats.push_back(data);
    }

    for(int x = 0;x < 4;x++)
    {
        flatData data;
        data.a = board[x][0][0];
        data.b = board[x][1][1];
        data.c = board[x][2][2];
        data.d = board[x][3][3];
        flats.push_back(data);
    }

    for(int y = 0;y < 4;y++)
    {
        flatData data;
        data.a = board[0][y][3];
        data.b = board[1][y][2];
        data.c = board[2][y][1];
        data.d = board[3][y][0];
        flats.push_back(data);
    }

    for(int x = 0;x < 4;x++)
    {
        flatData data;
        data.a = board[x][0][3];
        data.b = board[x][1][2];
        data.c = board[x][2][1];
        data.d = board[x][3][0];
        flats.push_back(data);
    }

    for(int z = 0;z < 4;z++)
    {
        flatData data;
        data.a = board[0][0][z];
        data.b = board[1][1][z];
        data.c = board[2][2][z];
        data.d = board[3][3][z];
        flats.push_back(data);
    }

    for(int z = 0;z < 4;z++)
    {
        flatData data;
        data.a = board[3][0][z];
        data.b = board[2][1][z];
        data.c = board[1][2][z];
        data.d = board[0][3][z];
        flats.push_back(data);
    }

    flatData data;
    data.a = board[0][0][0];
    data.b = board[1][1][1];
    data.c = board[2][2][2];
    data.d = board[3][3][3];
    flats.push_back(data);

    data.a = board[0][0][3];
    data.b = board[1][1][2];
    data.c = board[2][2][1];
    data.d = board[3][3][0];
    flats.push_back(data);

    data.a = board[3][0][0];
    data.b = board[2][1][1];
    data.c = board[1][2][2];
    data.d = board[0][3][3];
    flats.push_back(data);

    data.a = board[3][0][3];
    data.b = board[2][1][2];
    data.c = board[1][2][1];
    data.d = board[0][3][0];
    flats.push_back(data);

}

 

不难看出逻辑简单粗暴，直接遍历整个棋盘，并且将所有横竖斜的可能性加入FlatData的abcd四个位置中，再把该条加入到整个list中，为后续其他功能提供数据。

 

四、局势评分及输赢判断

在上一步的基础上，我们要做的是根据每组FlatData（展平后的数据格式）来给出我们评估的分数。

int whiteNum = 0,blackNum = 0;

    for(auto iter = flats.begin();iter != flats.end();iter++)
    {
        whiteNum = 0;
        blackNum = 0;

        if(iter->a == chessPicesStatus::black)
            blackNum++;
        else if(iter->a == chessPicesStatus::white)
            whiteNum++;

        if(iter->b == chessPicesStatus::black)
            blackNum++;
        else if(iter->b == chessPicesStatus::white)
            whiteNum++;

        if(iter->c == chessPicesStatus::black)
            blackNum++;
        else if(iter->c == chessPicesStatus::white)
            whiteNum++;

        if(iter->d == chessPicesStatus::black)
            blackNum++;
        else if(iter->d == chessPicesStatus::white)
            whiteNum++;

        if(whiteNum == 4)
            return chessPicesStatus::white;

        if(blackNum == 4)
            return chessPicesStatus::black;

    }

    return chessPicesStatus::empty;

以上为判断输赢的代码，可以看出就是在上一步的基础上添加了abcd四个位置白棋黑棋的统计，并且判断是否已经获胜。对于获取当前局面分评估的逻辑，其实只是在最后一步统计的时候更加细分一些：

int ChessBoard::getFlatPicesValue(PicesFlatDataList flats, chessPicesStatus status)
{
    int value = 0,whiteNum = 0,blackNum = 0;

    for(auto iter = flats.begin();iter != flats.end();iter++)
    {
        whiteNum = 0;
        blackNum = 0;

        if(iter->a == chessPicesStatus::black)
            blackNum++;
        else if(iter->a == chessPicesStatus::white)
            whiteNum++;

        if(iter->b == chessPicesStatus::black)
            blackNum++;
        else if(iter->b == chessPicesStatus::white)
            whiteNum++;

        if(iter->c == chessPicesStatus::black)
            blackNum++;
        else if(iter->c == chessPicesStatus::white)
            whiteNum++;

        if(iter->d == chessPicesStatus::black)
            blackNum++;
        else if(iter->d == chessPicesStatus::white)
            whiteNum++;

        if(status == chessPicesStatus::white)
        {
            //Calculating White Picess

            if(blackNum != 0)
                continue;

            if(whiteNum == 0)
                value += 1;
            else if(whiteNum == 1)
                value += 5;
            else if(whiteNum == 2)
                value += 100;
            else if(whiteNum == 3)
                value += 5000;
            else if(whiteNum == 4)
            {
                value += 100000;
            }

        }
        else
        {
            //Calculating Black Picess

            if(whiteNum != 0)
                continue;

            if(blackNum == 0)
                value += 1;
            else if(blackNum == 1)
                value += 5;
            else if(blackNum == 2)
                value += 100;
            else if(blackNum == 3)
                value += 5000;
            else if(blackNum == 4)
            {
                value += 100000;
            }

        }

        //cout<<iter->a<<" "<<iter->b<<" "<<iter->c<<" "<<iter->d<<" "<<value<<endl;
    }
    return value;
}

可以看出我们对于任何一个FlatData，如果该条数据有对方棋子存在，价值即为零，进入下一条。价值从本方棋子数目为零到四分别为1，5，100，5000，10000。

 

五、单个位置价值评分

 

为了实现后续的启发式搜索算法，我们需要计算出每个可下位置的得分，单个位置价值评分大体逻辑与上面两步基本一样，是先获取当前棋盘可落子的位置，接着遍历与之相连的各种可能性。但由于立体四子棋支持斜着四子连成，所以需要额外注意，此时展开需要分为SimpleFlat与Non-SimpleFlat。具体区别在于：

红色位置需要计算斜着连成的各种情况，而黑色区域的棋子不需要。所以在遍历时如果判断需要Non-SimpleFlat，则需要把更多的（斜着的若干种可能）添加到list中进行计算。

bool ifSimpleFlat(PicesPos pos)
{
    if(pos.x == 1 && pos.y == 0 ||
       pos.x == 2 && pos.y == 0 ||
       pos.x == 0 && pos.y == 1 ||
       pos.x == 3 && pos.y == 1 ||
       pos.x == 0 && pos.y == 2 ||
       pos.x == 3 && pos.y == 2 ||
       pos.x == 1 && pos.y == 3 ||
       pos.x == 2 && pos.y == 3)
        return true;
    else
        return false;
}

int ChessBoard::getPosValue(int board[4][4][4],PicesPos *pos, chessPicesStatus side)
{
    PicesFlatDataList flatList;

   // cout<<"x:"<<pos->x<<" y:"<<pos->y<<" z:"<<pos->z<<endl;
    if(ifSimpleFlat(*pos))
    {
        /*
        [0]   -
        [1]   |
        [2]   /-
        [3]   -\
        [4]   /_
        [5]   _\
        */
        flatData temp0;
        temp0.a = board[0][pos->y][pos->z];
        temp0.b = board[1][pos->y][pos->z];
        temp0.c = board[2][pos->y][pos->z];
        temp0.d = board[3][pos->y][pos->z];
        flatList.push_back(temp0);

        flatData temp1;
        temp1.a = board[pos->x][0][pos->z];
        temp1.b = board[pos->x][1][pos->z];
        temp1.c = board[pos->x][2][pos->z];
        temp1.d = board[pos->x][3][pos->z];
        flatList.push_back(temp1);

        flatData temp2;
        temp2.a = board[0][pos->y][0];
        temp2.b = board[1][pos->y][1];
        temp2.c = board[2][pos->y][2];
        temp2.d = board[3][pos->y][3];
        flatList.push_back(temp2);

        flatData temp3;
        temp3.a = board[0][pos->y][3];
        temp3.b = board[1][pos->y][2];
        temp3.c = board[2][pos->y][1];
        temp3.d = board[3][pos->y][0];
        flatList.push_back(temp3);

        flatData temp4;
        temp4.a = board[pos->x][0][0];
        temp4.b = board[pos->x][1][1];
        temp4.c = board[pos->x][2][2];
        temp4.d = board[pos->x][3][3];
        flatList.push_back(temp4);

        flatData temp5;
        temp5.a = board[pos->x][0][3];
        temp5.b = board[pos->x][1][2];
        temp5.c = board[pos->x][2][1];
        temp5.d = board[pos->x][3][0];
        flatList.push_back(temp5);

        flatData temp6;
        temp6.a = board[pos->x][pos->y][0];
        temp6.b = board[pos->x][pos->y][1];
        temp6.c = board[pos->x][pos->y][2];
        temp6.d = board[pos->x][pos->y][3];
        flatList.push_back(temp6);
    }
    else
    {
        /*
        [0]   -
        [1]   |
        [2]   /-
        [3]   -\
        [4]   /_
        [5]   _\
        [6]   -|/
        [7]   -|\
        */
        flatData temp0;
        temp0.a = board[0][pos->y][pos->z];
        temp0.b = board[1][pos->y][pos->z];
        temp0.c = board[2][pos->y][pos->z];
        temp0.d = board[3][pos->y][pos->z];
        flatList.push_back(temp0);

        flatData temp1;
        temp1.a = board[pos->x][0][pos->z];
        temp1.b = board[pos->x][1][pos->z];
        temp1.c = board[pos->x][2][pos->z];
        temp1.d = board[pos->x][3][pos->z];
        flatList.push_back(temp1);

        flatData temp2;
        temp2.a = board[0][pos->y][0];
        temp2.b = board[1][pos->y][1];
        temp2.c = board[2][pos->y][2];
        temp2.d = board[3][pos->y][3];
        flatList.push_back(temp2);

        flatData temp3;
        temp3.a = board[0][pos->y][3];
        temp3.b = board[1][pos->y][2];
        temp3.c = board[2][pos->y][1];
        temp3.d = board[3][pos->y][0];
        flatList.push_back(temp3);

        flatData temp4;
        temp4.a = board[pos->x][0][0];
        temp4.b = board[pos->x][1][1];
        temp4.c = board[pos->x][2][2];
        temp4.d = board[pos->x][3][3];
        flatList.push_back(temp4);

        flatData temp5;
        temp5.a = board[pos->x][0][3];
        temp5.b = board[pos->x][1][2];
        temp5.c = board[pos->x][2][1];
        temp5.d = board[pos->x][3][0];
        flatList.push_back(temp5);

        flatData temp6;
        temp6.a = board[pos->x][pos->y][0];
        temp6.b = board[pos->x][pos->y][1];
        temp6.c = board[pos->x][pos->y][2];
        temp6.d = board[pos->x][pos->y][3];
        flatList.push_back(temp6);

        if(pos->x == 0 && pos->y == 0 ||
           pos->x == 1 && pos->y == 1 ||
           pos->x == 2 && pos->y == 2 ||
           pos->x == 3 && pos->y == 3)
        {
            flatData temp7;
            temp7.a = board[0][0][0];
            temp7.b = board[1][1][1];
            temp7.c = board[2][2][2];
            temp7.d = board[3][3][3];
            flatList.push_back(temp7);

            flatData temp8;
            temp8.a = board[0][0][3];
            temp8.b = board[1][1][2];
            temp8.c = board[2][2][1];
            temp8.d = board[3][3][0];
            flatList.push_back(temp8);
        }
        else
        {
            flatData temp7;
            temp7.a = board[3][0][0];
            temp7.b = board[2][1][1];
            temp7.c = board[1][2][2];
            temp7.d = board[0][3][3];
            flatList.push_back(temp7);

            flatData temp8;
            temp8.a = board[3][0][3];
            temp8.b = board[2][1][2];
            temp8.c = board[1][2][1];
            temp8.d = board[0][3][0];
            flatList.push_back(temp8);
        }

    }

    int val = getFlatPicesValue(flatList,side);

    return val;

}

至此，我们已经完成了棋盘的评估函数，下一章我们将讨论极值搜索算法，也就是我们真正的博弈树函数。