编译原理之语法分析-自下而上分析(二)

、　　　　（一）LR分析法

　　　　  LR分析定义：从左到右扫描(L)输入串，构造最右推导的逆过程(R)，是自下而上分析法的核心。

　　　　  LR分析法特点：

• • 严格的规范规约。
  • 比递归下降分析法、LL(1)分析法对文法的限制要少得多，适用范围广，适用于大多数上下文无关文法描述的语言。
  • 分析速度快，能准确定位错误。

　　　　  LR分析法缺点：手工构造分析程序工作量相当大。

　　　　  LR分析器的组成：

• • 总控程序：执行分析表所规定的动作，对进行操作。所有的LR分析器相同。
  • 分析栈：又分为符号栈和状态栈。
    • 符号栈：存放分析过程中移进或归约的符号。
    • 状态栈：状态栈存放的是状态(标记号)，记录分析过程中从开始的某一归约阶段的整个分析历史或预测扫描了能遇到的分析符号
  • 分析表：LR分析器的核心。其功能指示分析器是移进还是规约，根据不同的文法类要采用不同的构造方法。(后边会具体描述)

　　　　  LR分析器模型：

　　　　  

 

 

 

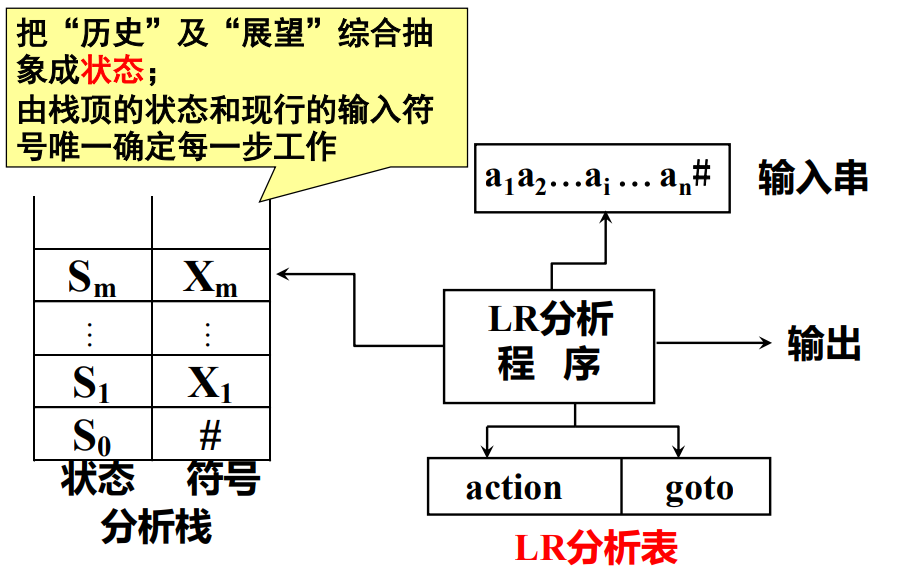
　　　　  根据上图可以看出LR分析程序依次将输入串以及当前状态移入分析栈，然后根据分析栈和当前输入串去查找分析表去判断下一步应该进行什么操作。

　　　　  我们最终的目的是通过一系列操作去构造这个LR分析表。

 

　　　　  四种LR分析方法以及范围：在后续博客中我们会依次讲解LR(0)、SLR(1)、LR(1)。

　　　　  图中看出一个LR(0)文法必定是SLR(1)、LALR(1)和LR（1）文法；LALR(1)文法必定是LR(1)文法。

　　　　  

　　　　  (二)LR(0)分析法基本概念

　　　　  LR(0)定义：从左到右扫描(L)输入串，构造最右推导的逆过程(R)，0代表不向前看任意符号即不进行展望或预测。

　　　　  LR(0)分析法流程（移进-归约）：

• • 识别活前缀（目的是为了寻找句柄）NFA->DFA->项目集规范族(DFA的元素)
  • CLOSURE（求规范族）->GO（DFA边）
  • 构造LR（0）分析表

　　　　   同样先讲解几个定义:活前缀、增广文法(拓广文法)、LR(0)项目。

• • 活前缀(可归前缀)：目的是为了寻找LR分析中可归约串(句柄)，采取归约过程前符号栈中的内容，称为可归前缀。这种前缀包含句柄且不包含句柄之后的任何符号。

　　　　

　　　　    为了加强对活前缀定义的理解，我们举个例子。

文法G(E):
    E->E+T | T
    T->T*F | F
    F->(E) | id
句型E+id*id的活前缀是什么？
答案：E、E+、E+id

　　　　  

 

 

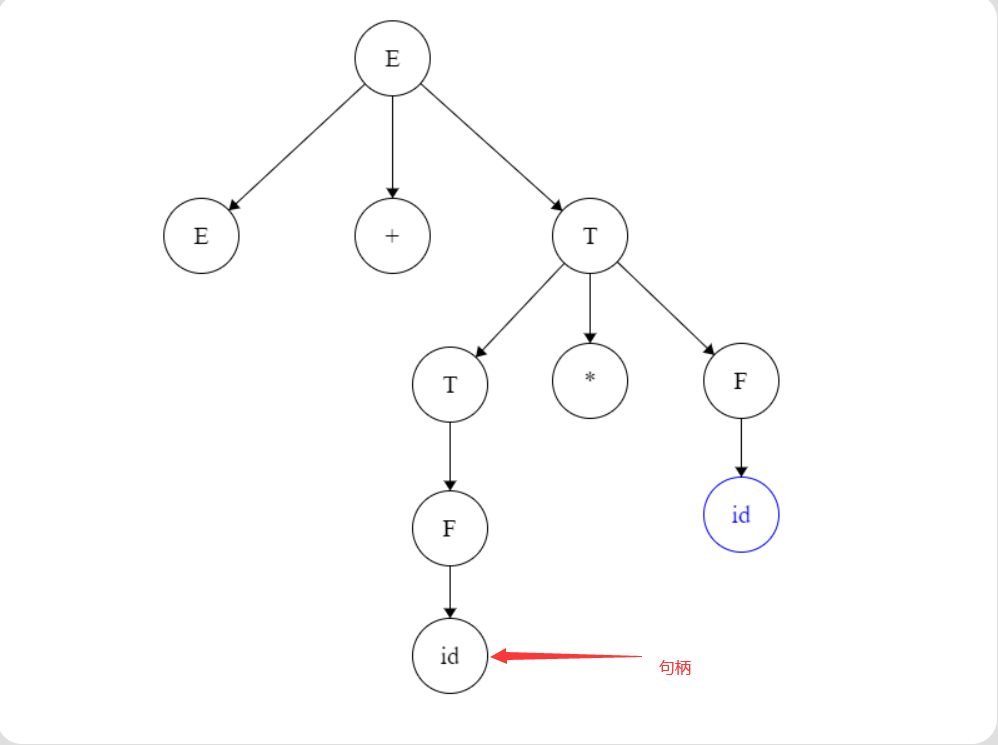
 　　　　先画出句型E+id*id的语法树，如上图。

　　　　 根据定义，前缀的尾符号最多包含到句型的句柄。从图中可以得出句型E+id*id的句柄是id。

　　　　 这里有个方法(个人见解，如果错误及时提出)：我们找到句柄(id)之后查看它左侧的所有叶子节点，即本例中的E和+，然后将E、+、id(句柄)按从左到右的顺序组合成E+id。

　　　　 组合完之后我们要找的活前缀就是E+id的所有前缀串：E、E+、E+id（前缀串包括本身）。这样就得出了活前缀。

• • 增广文法：假定文法G是一个以S为开始符号的文法，构造一个新的文法G‘,称G'是G的增广文法，G'定义如下。
    • 只增加一个新的非终结符S’(G‘的开始符号)；
    • 增加一个新的产生式S’->S；
    • 增广文法会有一个仅含项目S'->S·的状态，这是唯一的接受态；

　　　　 　　　 例如文法G(S): S->aAc

　　　　　　　  ①添加一个新的文法G'(S')

　　　　　　　  ②添加新的产生式S’->S

　　　　　　　  ③新的文法:G‘（S’）：S' -> S  ， S -> aAc

 　　　　　　　 文法G’就是G的增广文法，这样做的目的是为了保证 开始符号指向非终结符；也就是说如果不使用增广文法，无法确保开始符号一定能推导出非终结符，比如例子中文法G如果改为S -> aac，这样就是开始符号指向终结符。

• • LR(0)项目集:在文法G中每个产生式的右部适当位置添加一个圆点构成项目。

　　　　　　　  每个项目的含义是：欲用改产生式归约时，圆点前面的部分为已经识别了的句柄部分，圆点后面的部分为期望的后缀部分。

　　　　　　　

 

 

 　　　　　　　　LR(0)项目分类：

• • • • 移进项目：A->α• aβ，圆点后边为终结符，对应移进状态，把a移进符号栈。
      • 待约项目：A -> α • Bβ，圆点后边为非终结符，对应待约状态，需要等待分析完非终结符B之后再继续分析A的右部，相当于在语法树中进入B的子节点。
      • 归约项目：A -> α •，圆点在产生式最后，形成了可归前缀(句柄)，进入归约状态。
      • 接受状态：S'->S•，如果接受一个S(最终规约)则进入接受状态。
      • 初始状态：S'->•S 。
      • 有效项目：通过下面两幅图来说明有效项目。

　　　　　　　　　　

　　　　　　　　　　

　　　　　　　　　　　　对于B->•cB和B->•d这两个项目对于活前缀bc的无效。因为圆点之前没有活前缀bc的前缀串。

  　　　　(三)LR(0)构造分析表(通过例子讲解构造分析表的流程)

　　　　　　 有一文法G（E）: E->AE | b ，A->a

 　　　　　　1、构造增广文法

　　　　　　　　G(S): S -> E#(#为结束符号) ，  E->AE | b ，A->a

　　　　　　 2、列出增广文法的项目集(注意圆点的位置，为了方便下边构造NFA，将每个项目编号)

1)    S->·E
2)    S-> E·
3)    E->·AE
4)    E-> A·E
5)    E-> AE·
6)    E->·b
7)    E-> b·
8)    A->·a
9)    A-> a·

　　　　　　 3、构造识别活前缀的NFA

 　　　　　　

 

　　　　　　 如果构造识别活前缀的NFA？这里可以分两种情况

　　　　　　　　Ⅰ、指向下一项目条件为空串(例如图中1指向3和6)

　　　　　　　　　　从开始符号即项目1开始，圆点位置后边为E(非终结符)，即这是一个待约项目。这时需要将1指向(输入条件为空串)满足以下产生式的项目。

• • • • 产生式左部为E
      • 产生式右部第一个为圆点

　　　　　　　　　 　　 满足以上两个条件的项目，输入条件为空。即图中项目1指向3和6。因为1圆点后边为非终结符E，且项目3和6产生式左侧为E，产生式右侧第一个为圆点(以圆点开始)。

　　　　　　　 　　 　　而项目1不能指向4、5、7原因是因为这三个项目产生式右侧不是以圆点开始的。不能指向8的原因是因为8的产生式左侧不是E。

　　　　　　　　Ⅱ、指向下一项目条件不为空串(例如图中1指向2，说明输入了终结符活非终结符，从而进入了下一个状态)

　　　　　　　　　　　  当状态转换条件不为空串时，说明读取了一个输入字符，从而进入了下一个状态。例如项目8读入一个字符a之后圆点后移，正好就是9，因此8->9的条件是输入符号a。

　　　　　　4、构造识别活前缀的DFA(注意：DFA和NFA的状态编号没有任何联系，DFA状态编号对应项目编号，NFA编号可自己定义但要按顺序)

 

 　　　　　　　　

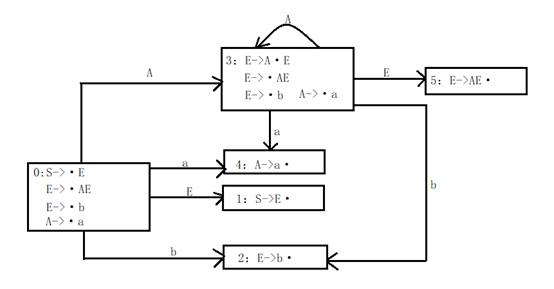
 　　　　　　　　构造DFA有两种方法：

　　　　　　　　　　Ⅰ、根据NFA构造DFA

　　　　　　　　　　　　DFA同样是从S->·E（开始符号）开始。那么在DFA的状态0中为什么会有，E->·AE、E->·b和A->·a呢？

　　　　　　　　　　　　当我们查看NFA时可以发现，项目1(S->·E)经过任意个空串之后能够到达项目3、6、8，查看项目集可以发现项目3、6、8正好是E->·AE、E->·b和A->·a。

　　　　　　　　　　　　因此可以得出结论，根据当前状态，如果经过任意个空串之后能后到达的状态属于同一个DFA状态(即属于DFA中的同一个方框)。

　　　　　　　　　　　　如果还没有明白的话，我们再使用DFA的状态3作讲解。

　　　　　　　　　　　　状态0输入A之后可以从E->·AE转为状态3 E->A·E，这时先将E->A·E写入方框，然后查看NFA看项目E->A·E经过任意空串能达到哪个项目，并将对应的项目写入E->A·E所在方框；

　　　　　　　　　　　　可以发现项目E->A·E(即项目4)经过任意空串可以到达3、6、8。因此将项目3、6、8写入E->A·E所在方框。

　　　　　　　　　　Ⅱ、不根据NFA构造DFA(一般情况下，构造NFA比较耗时，所以及时不构造NFA也能写出DFA)

　　　　　　　　　　　　同样从S->·E开始，将S->·E写入方框。

　　　　　　　　　　　　①发现圆点后边为非终结符E，这时寻找满足以下两个条件的产生式：1、产生式左部为E；2、产生式右部以圆点为开始；

　　　　　　　　　　　　②根据①讲满足条件的E->·AE和E->·b写入方框。

　　　　　　　　　　　　③发现E->·AE这个项目圆点后还有非终结符A，这时再寻找产生式左部为A，右部以圆点开始的产生式，经过寻找讲A->·a加入方框。

　　　　　　　　　　　　这样不断迭代，直到方框中圆点后均为终结符(A->·a、E->·b)或者圆点后为终结符但是它的下一个状态已经被我们加入方框，这样这个状态的方框已经画完。然后我们再根据圆点位置判断下一个要输入的符号。

　　　　　　5、根据构造好的DFA判断该文法是不是LR(0)文法

　　　　　　　　Ⅰ、判断LR(0)文法的依据，活前缀识别自动机(DFA)中每个状态(项目集)不存在下述两种情况：

　　　　　　　　　　①既含移进项目又含归约项目；

　　　　　　　　　　②含有多个归约项目；

　　　　　　　　　　如果能同时满足以上两点则，该文法就是一个LR(0)文法。

　　　　　　　　 Ⅱ、举一个反例：

　　　　　　　　　　

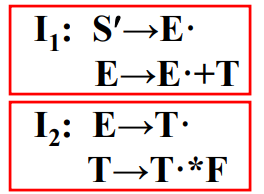
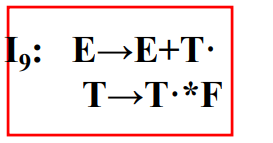
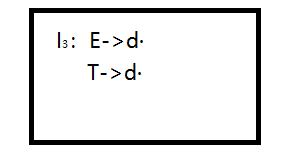
 　　　　　　　　　　 有如上四个项目集，前三个项目集均不满足上述第一条，最后一个不满足上述第二条。

　　　　　　　　　　  项目集1：S‘ -> E· 是一个归约项目，但是在该项目集中还存在E -> E· + T；这时就会有冲突，当我们输入字符E的时候，我们下一步是要进行对S->E' 的归约呢，还是要继续读入E -> E ·+ T中的终结符+(移进)呢？这样就会存在冲突。

　　　　　　　　　　  项目集2：同样，当输入T之后，我们是要对E->T·进行归约，还是继续将T->T· * F中的终结符*读入栈(移进)呢？这也存在冲突。

　　　　　　　　　　  项目集9：同上，无法判断要对E->E+T·进行归约，还是对T->T·*F中的*进行移进操作。

 　　　　　　　　　　 项目集3：当输入字符d之后，是要将d归约为E，还是归约为T呢？这同样也存在着冲突。

　　　　　　　　　　  判断LR(0)文法总结：可以发现前三个项目集都是无法判断下一步要进行归约还是移进，这种冲突称为移进-归约(s-r)冲突。

　　　　　　　　　　　　　　　　　　　　第四个项目集，无法判断下一步要归约为哪一个产生式，因此这种冲突称为归约-归约(r-r)冲突。

　　　　　　　　　　  只要某个文法项目集存在上述两种冲突的任意一个都不是LR(0)文法。

　　　　　　6、判断之后，该文法如果是LR(0)文法，则根据规则构造LR(0)分析表。

　　　　　　　  某文法描述如下：

　　　　　　　　　

　　　　　　　这里有一个项目集，我们使用该项目集构造分析表。

　　　　

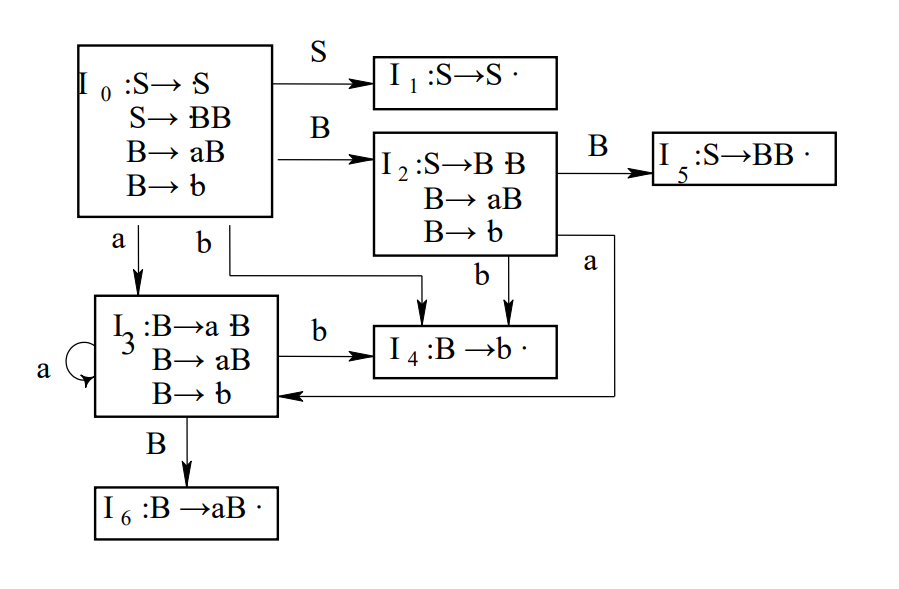
　　　　　　　　   首先需要知道分析表的结构：

　　　　　　　　　　①表头有ACTION，和GOTO动作，ACTION下的列写的是终结符，GOTO下的列写的是非终结符；ACTION有三个状态移进(s)、归约(r)和接受（acc），GOTO中直接写项目集编号。

　　　　　　　　　　②第一列是DFA中项目集的编号(状态编号)。

　　　　　　　　   直接给出该项目集分析表然后我们一步一步讲解。

　　　　　 

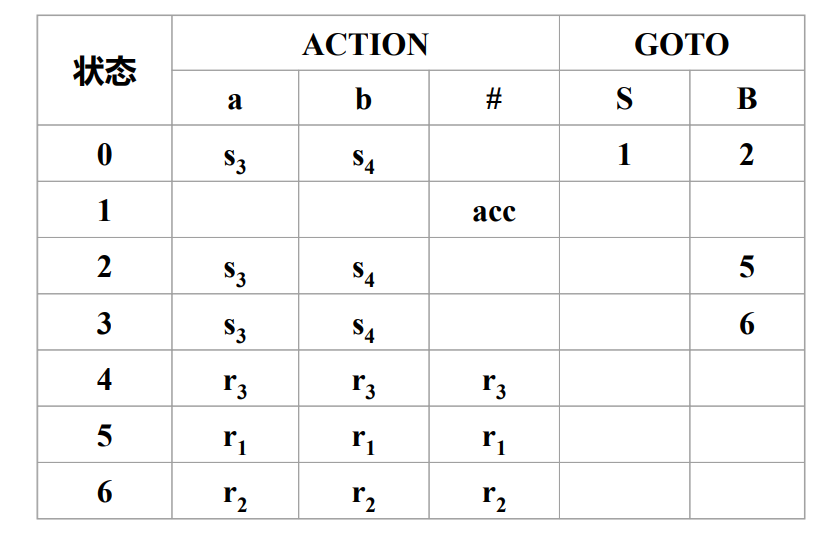
1. 1. 1. 从状态0开始，当遇到字符串a，将a移进，同时转换为成状态3，所以在对应的表中位置就写入s3。
      2. 当状态0遇到字符b时，将b移进，同时转换为状态4，在对应表中位置写入s4。
      3. 当状态0遇到非终结符B，跳转到状态2，在状态0所在行GOTO表的B所在列，直接写状态编号2即可。
      4. 当状态0遇到S，跳转到状态1，GOTO表中直接写状态编号1。　
      5. 状态1为接受状态，期望输入一个#号，因此在#号位置写入acc(接受状态)。
      6. 状态2遇到字符a，将a移进，同时转换为状态3，在对应表中位置写入s3。　
      7. 状态2遇到字符b，将b移进，同时转换为状态4，在对应表中位置写入s4。
      8. 当状态2遇到非终结符B，跳转到状态5，在状态2所在行GOTO表的B所在列，直接写状态编号5即可。
      9. 状态3遇到字符a，将a移进，同时转换为状态3，在对应表中位置写入s3。　
      10. 状态3遇到字符b，将b移进，同时转换为状态4，在对应表中位置写入s4。
      11. 当状态3遇到非终结符B，跳转到状态6，在状态3所在行GOTO表的B所在列，直接写状态编号6即可。
      12. 因为状态4、5、6为归约项目，所以4、5、6所在行接受任意终结符都进行归约。例如状态2接受B跳转到状态5，在表中就是GOTO5，然后这时按照文法规则(1)(上上图中的文法对应的编号)进行归约，表格中写入r1。
      13. 同理在状态4中，终结符对应的每一列写入r3，状态6中终结符对应的每一列写入r2。

　　　　　　　　  经过一系列操作，我们的LR(0)分析表就已经构造完成。以上就是构造LR(0)分析表所需要的六个步骤。

 

 　　　　　　　　 以上均为个人学习总结，如有错误或异议欢迎提出（自下而上分析法未完待续......）。