bayes实现手写数字识别

一。贝叶斯基本理论

二。看一个简单的例题，只有一个特征(长度)。

 

 

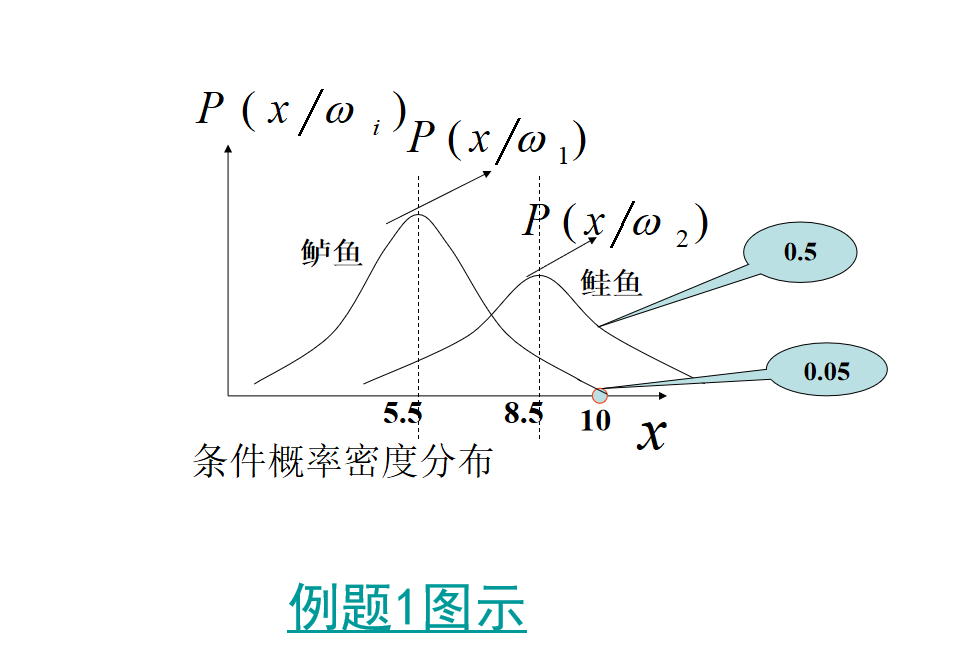
对于贝叶斯方法来说，首先要知道类别的先验概率，和类概率。

对于上述例题来说，p（x=10|w1）和p（x=10|w2）是已知的，但是拿到别的例子来说，这个是需要我们自己计算的。通过多个样本，计算类概率密度，其实就是训练的过程。

例题只有一个特征，而大多数情况不止有一个特征，我们则需要计算p(X|wi）X={x1,x2,x3……xn}。X是特征向量，包括N个特征。每个特征有不同的取值。

通常来说，我们需要假设特征之间是相互独立的，即朴素贝叶斯，P(X|wi)等价为P(x1|wi)*P(x2|wi)*P(x3|wi)……*P(xn|wi);

举个例子：我们现在有猫和狗两类，特征有高度（100和50两个取值）和重量（100和50两个取值）两种。训练样本有2个(用于计算类概密)，还有2个测试样本。

 

 根据所给样本得到的类概密，去计算测试样本的对应于不同类别的后验概率，得到概率最高的类别，判定为结果，计算时，因为分母相同，所以可以忽略。

 

 

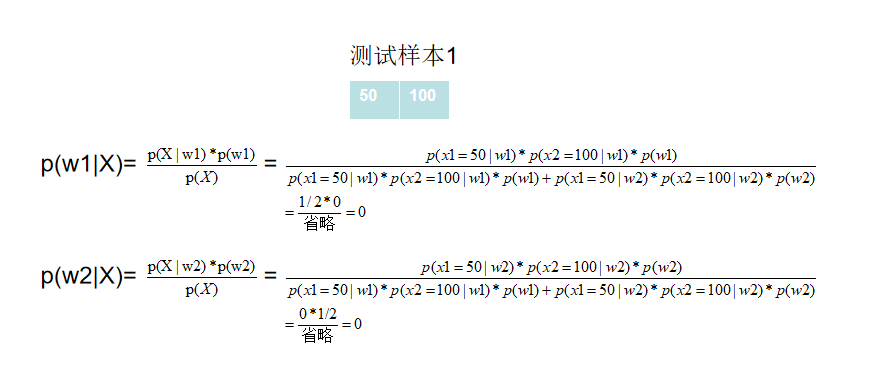
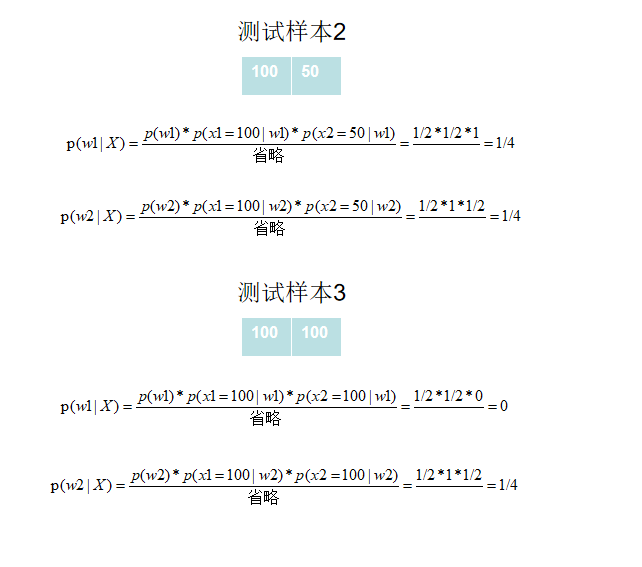
 样本1，2无法判定，样本三为狗。

 三。使用贝叶斯进行手写数字识别。

 

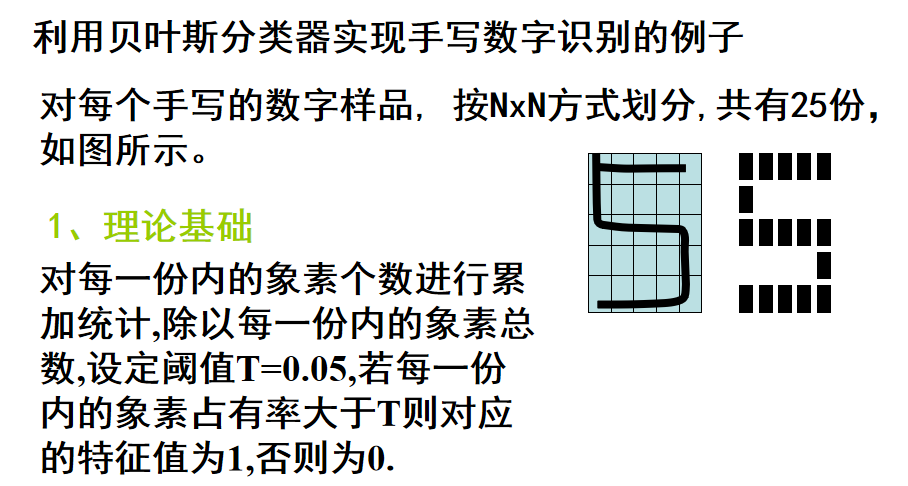
 准备条件：我下载了MNIST数据集，并转化为了PNG图片，分为0-9，10个类别。每张图片28*28像素。

手动设定划分数和阈值。

比如长和宽各7划分，一个将28*28分成49个区域，每个区域看作一个特征，每个区域共有4*4=16个像素。阈值设定为0.18，意思是如果16个像素中，有超过3个像素中是有笔画的，则这块区域的特征值为1，否则为0；

和前面的例子比较，这里只是把2个特征（高度和体重），换成了49个特征。把取值100和50，换成了1和0；

通过转换，可以得到图像7*7的特征图。

在这里p(x1=1|W1)，为N个样本中特征1为1的比率。p(x1=0|W1)=1-p(x1=1|W1);依次计算49个特征为1的比率，可以用一个数组来存放49个特征值为1概率。

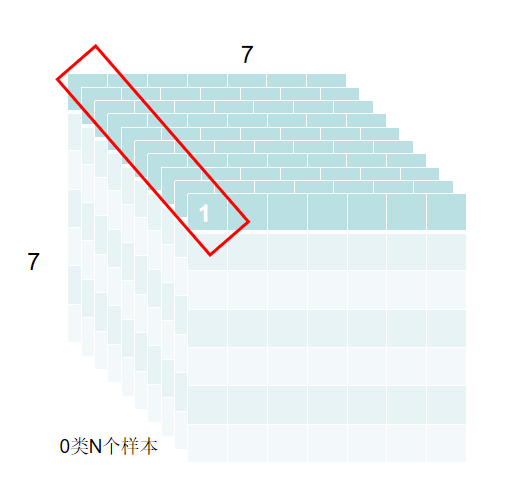
 分别计算10个类别的不同特征的概率，可以得到一个10x49的二维数组。

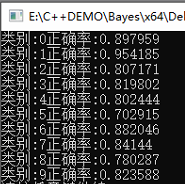
当测试一张新的图片时，先根据前面的步骤，将28*28的转换成一个7*7的特征图，然后根据贝叶斯公式。可以计算p(wi|X),求Max(p(wi|X))

因为数组中只有特征值为1的概率，特征值为0的只需要用1减去当前特征值为1的概率。

 

原图：28*28，特征图14*14，写程序时做了14划分，特征更多效果会好一点。