AC自动机学习笔记-1(怎么造一台AC自动机?)
月更博主又来送温暖啦QwQ
今天我们学习的算法是AC自动机。AC自动机是解决字符串多模匹配问题的利器,而且代码也十分好打=w=
在这一篇博客里,我将讲解AC自动机是什么,以及怎么构建一个最朴素的AC自动机。(不知道为什么我写出来的AC自动机常数就是大得要命=。=)
前置知识
首先你一定要对Trie树以及KMP了如指掌,尤其是要明白KMP中失配数组(next或fail数组)的本质:利用已经匹配过的部分,跳过重复的匹配,达到快速匹配的目的。
AC自动机是什么
大家都知道KMP可以用于在一个大字符串(文本串)中寻找另一个小的字符串(模式串),那么如果有n个模式串,要你把它们全部在文本串中找出来呢?当然,我们可以做n次KMP(别小瞧30分哦),但是其效率并不能差强人意。这个时候,我们可以尝试把模式串做成Trie树,似乎可以提高效率。
比如说,我们有5个模式串:she,shr,say,he,her,那么它们所建出来的Trie树应该是长成这样的:(红色节点表示单词的结尾)
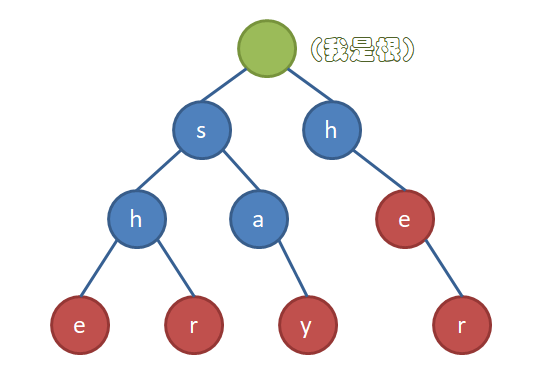
那么,怎么用它来匹配呢?如果我们把文本串的每一个点都作为起点放到Tire树上匹配,它的复杂度将会是...我要你Tire树有何用(╯‵□′)╯︵┻━┻
既然这样,那么如果只把文本串的第一个字符为起点,会发生什么呢?
你以为会是这样的:
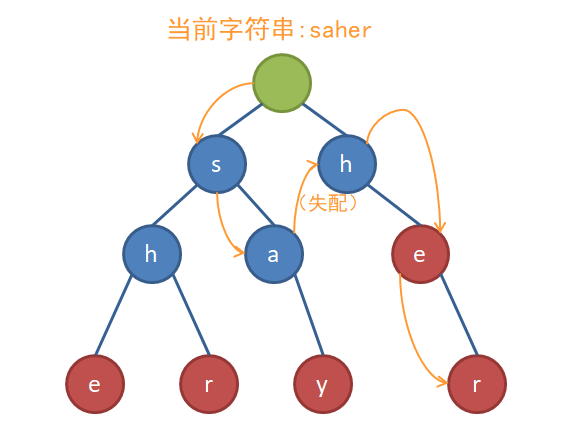
完美!
然而实际上却是这样的:

问题很明显,当我们匹配完she时,he其实也被匹配到了。所以我们希望这棵Trie树上能够加点东西,让它可以达到下面的效果:
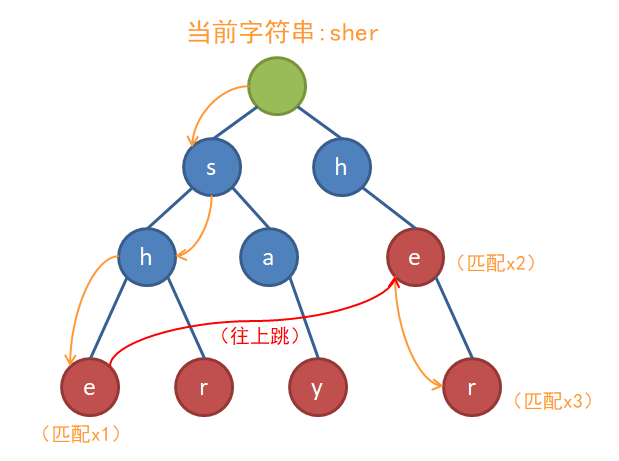
上图中,红色的箭头就是失配指针——fail指针。它表示文本串在当前节点失配后,我们应该到哪个节点去继续匹配。很显然,对于每个节点,我们要找到这个节点-代表的字符串-在树上所有的节点-表示的字符串中-能找到的最长的后缀,意思就是“我当前匹配到了这个点,我也相当于匹配到了的节点(中的深度最大的节点)。”比如说,在我举的例子中,当我们匹配到了she时,我们在树上走的路径也包含了he,he是she的一个后缀。我们在she上失配,至少说明我们已经匹配到了he,于是就可以跳到代表he的节点上继续匹配。
到这里,你是不是发现fail指针和KMP中的next指针简直一毛一样?它们都被称为“失配指针”。将Trie树上的每一个点都加上fail指针,它就变成了AC自动机。AC自动机其实就是Trie+KMP,它可以用来解决在文本串中寻找很多模式串,即多模匹配问题。
对于一开始的5个单词,它们所构建出的AC自动机就长这样(没有画出红色箭头的点,其fail指针都指向根节点):

如何构建AC自动机
显然,我们要做的就是快速地求出所有点的fail指针。我们以bfs的顺序依次求出每个节点的fail,这样,当我们要求一个节点的fail时,它的父亲的fail肯定已经求出来了。若当前节点为A,其父节点为B,B的fail为C,那么C所代表的字符串一定是B的最长的后缀。如果C有一个儿子D的字符与A的字符等同,那么显然D所代表的串(C加一个字符)就是A所代表的串(B加一个字符)的最长后缀。如果C没有一个儿子,使其字符与A的字符等同呢?很简单,只需要再访问C的fail就行了。如此反复,直到A的最长后缀找到,或者A的fail指向根节点为止。(A在Trie树中没有后缀,乖乖回到根重新匹配吧!)
为了解释得更清楚,我举一个例子。下面这幅图是我根据别的地方的图重新画的(n次转载?),出处我没找到_(:з」∠)_。节点是根据bfs序标号的。
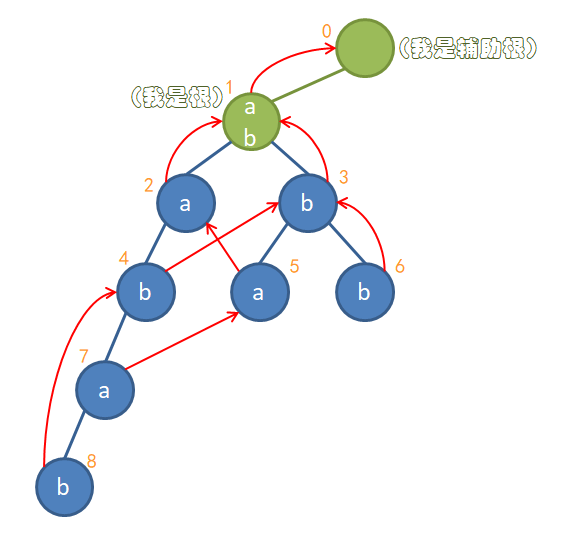
步骤:
- 为了少一些特判,设置一个辅助根节点0号节点,0号节点的所有儿子都指向真正的根节点1号节点,然后将1号节点的fail指向0号节点。
- 找到2号节点的父亲节点的fail节点0号节点,看0号节点有没有为a的子节点。有,于是2号节点的fail指向1号节点。
- 找到3号节点的父亲节点的fail节点0号节点,看0号节点有没有为b的子节点。有,于是3号节点的fail指向1号节点。
- 找到4号节点的父亲节点的fail节点1号节点,看1号节点有没有为b的子节点。有,于是4号节点的fail指向3号节点。
- 同上。
- 同上。
- 同上。
- 找到8号节点的父亲节点的fail节点5号节点,看5号节点有没有为b的子节点。没有,于是再找到5号节点的fail节点2号节点,看2号节点有没有为b的子节点。有,于是8号节点的fail指向4号节点。
这样,一个AC自动机就做好了。
注意到由于辅助节点的存在,我们不需要做任何特判,在树上没有后缀的节点的fail指针会自动连向根节点。
构建fail指针的代码:
void build()
{
for(int i=0;i<26;++i)ch[0][i]=1;
fail[1]=0;
queue<int>q;
q.push(1);
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=0;i<26;++i)
{
int c=ch[x][i];
if(!c)continue;
int fa=fail[x];
while(fa&&!ch[fa][i])fa=fail[fa];
fail[c]=ch[fa][i];
q.push(c);
}
}
}
如何利用AC自动机来查找
这个问题似乎显而易见,只要根据文本串的内容沿着Trie树的边往下走就行了,一失配就沿着fail边向上跳。
。。。
我在被大佬虐飞之前也是这么想的QwQ
fail边不只是失配指针这么简单,如果你像我刚才说的那么做的话,你就可能会面临下面这样的问题:
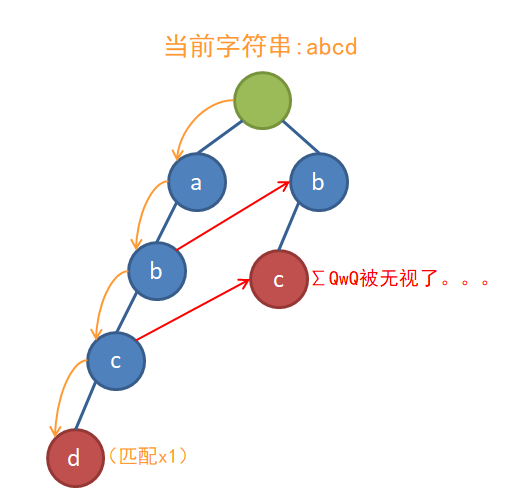
为了不让这种事情发生,我们每遇到一个fail指针就必须向上跳到顶,以保证不会漏过任何一个子串,就像这样:
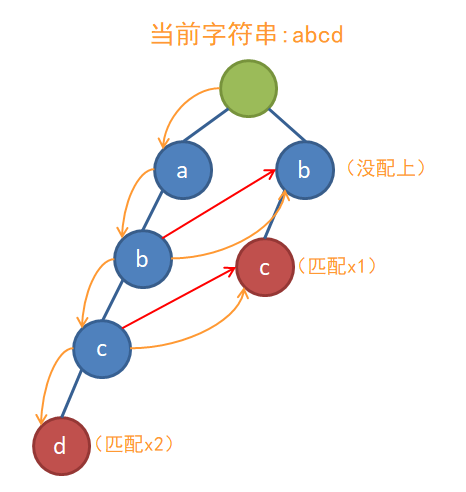
当然,这样未免也太蠢了,于是这里又有一个小优化:如果一个节点的fail指向一个结尾节点,那么这个点也成为一个(伪)结尾节点。在匹配时,如果遇到结尾节点,就进行相应的计数处理。
进行匹配的代码:
void print(int x)
{
while(x)
{
if(end[x])
{
//计数、打印等等,视题目要求而定
}
x=fail[x];
}
}
void match(char *s)
{
int len=strlen(s),now=1;
for(int i=0;i<len;++i)
{
int id=s[i]-'a';
while(now&&!ch[now][id])now=fail[now];
now=ch[now][id];
if(end[now]||en[now])print(now);
//en[now]即为伪结尾标记
}
}
//记得在build中加上这句话
void build()
{
...
if(end[fail[c]]||en[fail[c]])en[c]=1;
...
}
一个被我们忽略的问题
时间复杂度???
设模式串平均长度为 $ l $ ,建树复杂度为 $ O(nl) $ ,构建fail指针为 $ O(nl) $ ,匹配时因为每次都要跳fail边,复杂度上界可以达到 $ O(ml) $ ,所以总复杂度为 $ O((n+m)l) $ !
这和暴力有什么区别(╯°Д°)╯︵┻━┻???
虽然说,这个上界应该是十分松的,但是我们想要的是能跑 $ 1e6 $ 的速度!
这个时候我们就需要优化了。。。然而我已经没时间写辣QwQ!这些就留到下一篇博客吧!
谢谢你的资瓷啦QwQ!





