Dynamic Rankings || 动态/静态区间第k小（主席树）

JYF大佬说，一星期要写很多篇博客才会有人看

但是我做题没有那么快啊QwQ

Part1 写在前面

区间第K小问题一直是主席树经典题=w=今天的重点是动态区间第K小问题。静态问题要求查询一个区间内的第k小的值（可重），动态问题还要求支持单点修改操作。

这个问题也可以用线段树+Splay/整体二分解决，然而那些对蒟蒻来说都太难辣QwQ，这里给一个XZY大佬的整体二分的讲解传送门

我们的做法是主席树+树状数组，如果有不会主席树的同学可以看我之前写的博客=w=，由于静态问题是动态问题的基础，所以我会先讲静态的怎么做，如果你已经对静态区间第k小问题了如指掌的话就可以跳过Part2直接看重点啦=w=

Part2 静态区间第k小

这个其实很简单，我们的每一棵主席树都是一棵权值线段树，第 $ i $ 棵主席树的每个叶子节点都存储对应的（离散化后的）值在序列前缀 $ [1,i] $ 中出现的次数，例如第 $ i $ 棵主席树的 $ j $ 个叶子节点就存储数值 $ hash[j] $ 在区间 $ [1,i] $ 中出现的次数。内部节点存储的则是两个儿子的值的和，例如表示区间 $ [l,r] $ 的内部节点存储的是 $ hash[l到r] $ 的所有数在序列 $ [1,i] $ 中出现的次数总和。

建树时，我们将序列的值离散化，主席树的时间维表示原序列坐标，从左到右依次插入。如果要查询前缀 $ [1,r] $ 中的第k小，就相当于在第 $ r $ 棵主席树上进行一个类似于splay的kth操作：看看当前节点 $ [l,r] $ 的左儿子的值 $ size $ ，如果大于等于k，说明当前区间第k小为 $ [l,mid] $ 中的第k小，反之则为 $ [mid+1,r] $ 中的第（k-size）小。这样不停地递归子区间，最后我们会来到一个叶节点，它就是我们要找的第k小了。那么，如果要查询区间 $ [l,r] $ 中的第k小的话，只需同时在第 $ r $ 与第 $ l-1 $ 棵主席树上进行kth，将 $ size $ 值相减后与k比较即可。

这么说可能不太直观，来一段代码：

void insert(int l,int r,int &x,int y,int tar)//x:当前位置i代表的root，y:i-1，tar:a[i]离散化后的位置
{
    x=++cnt,node[x]=node[y],++node[x].x;
    if(l==r)return;
    int m=(l+r)>>1;
    if(tar<=m)insert(l,m,node[x].l,node[y].l,tar);
    else insert(m+1,r,node[x].r,node[y].r,tar);
}

int query(int l,int r,int x,int y,int size)//size即为第k小的k，x、y为两棵主席树当前遍历到的节点
{
    if(l==r)return l;
    int m=(l+r)>>1,tmp=node[node[y].l].x-node[node[x].l].x;
    if(tmp>=size)return query(l,m,node[x].l,node[y].l,size);
    else return query(m+1,r,node[x].r,node[y].r,size-tmp);
}

Part3 动态区间第k小

请确保你已经完全掌握了静态区间第k小问题，推荐SPOJ的COT这一题作为练习QwQ

在静态问题中，我们所建出来的主席树（们）所表示的区间长这样：

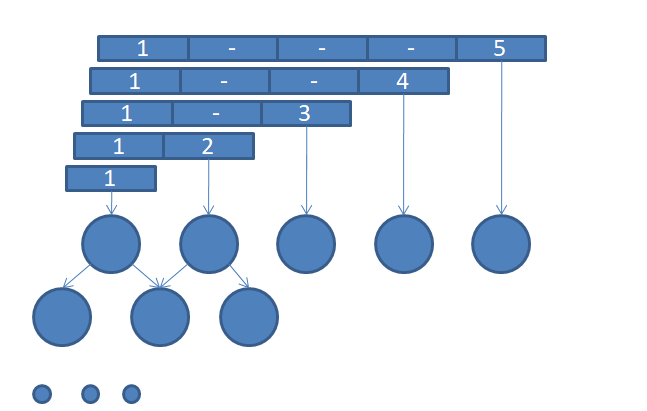
如果要修改原数组上的一个点，我们就必须一连修改包含它的n棵主席树，一次修改的复杂度就达到了 $ O(nlog_2n) $ 。我们要想办法使得一次修改不需要改那么多树。

emmmm...

查询前缀和，一次修改 $ log_2n $ 个节点，那岂不是。。。

树状数组：没错，就是我！

如果我们像这样划分每棵主席树所代表的区间：

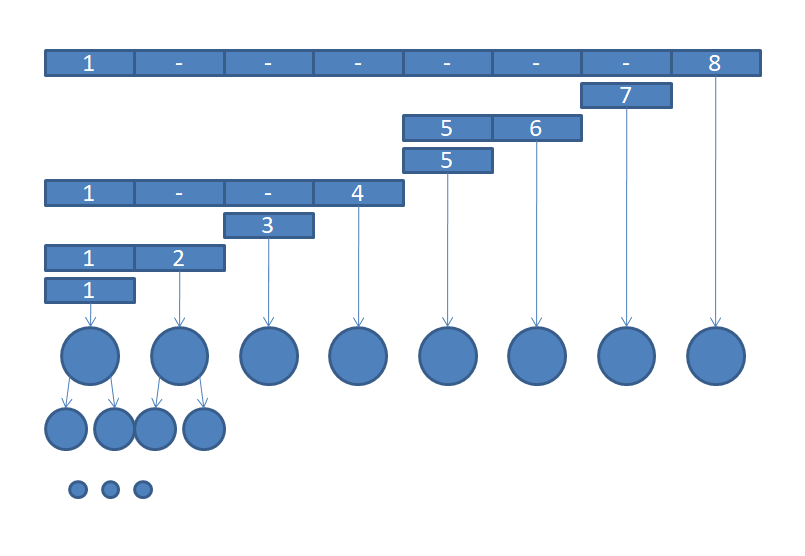
显然，原序列的一个点最多被包含在 $ log_2n $ 棵主席树中，我们要查询区间 $ [l,r] $ 时则需要计算出 $ l-1 $ 与 $ r $ 的前缀和再相减即可。这两个操作的复杂度都变成了 $ O(long^2_2n) $ 。而且，树状数组编程复杂度极低，我们不需要真的写一个数据结构，只需要在主席树中运用lowbit函数就行了。

注意，这种划分方式使得每一棵主席树之间没有了公共部分，它们其实已经不能称之为主席树了，不如说是很多棵动态开点的线段树放在一起。然而，为了节省空间与时间（ZOJ上空间限制为丧心病狂的32MB），我们可以初始化一棵静态的主席树，只用套了树状数组的主席树来维护修改。其他的细节就看代码吧。

代码（ZOJ可AC）：

#include <cstdio>
#include <cstring>
#include <abstergo>
#define R register
using namespace std;
const int MAXN=50050;
const int inf=0x3f3f3f3f;
int a[MAXN*2],X[MAXN*2],top;
int n;

template<class T>void read(T &x)
{
	x=0;int ff=0;char ch=getchar();
	while(ch<'0'||ch>'9'){ff|=(ch=='-');ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	x=ff?-x:x;
}

void readc(char &ch)
{
	ch=getchar();
	while(ch<'A'||ch>'Z')ch=getchar();
}

struct asks
{
	char ch;
	int t1,t2,t3;
}ask[MAXN];//存储询问

inline int lowbit(int x)
{return x&(-x);}

int find(int x)
{return lower_bound(X+1,X+1+top,x)-X;}

class CMT
{
private:
	int root1[MAXN*2],root[MAXN*2],bitr[50],bitl[50],cnt;
	
	struct CMT_node
	{
		int l,r,x;
	}node[MAXN*50];
	
	void insert(int l,int r,int &x,int y,int tar,int del)
	{
		if(!x||x==y)x=++cnt,node[x]=node[y];
		node[x].x+=del;
		if(l==r)return;
		int m=(l+r)>>1;
		if(tar<=m)insert(l,m,node[x].l,node[y].l,tar,del);
		else insert(m+1,r,node[x].r,node[x].r,tar,del);
	}
	
	int query(int l,int r,int x,int y,int size,int len1,int len2)
	{
		if(l==r)return l;
		int m=(l+r)>>1,tmp;
		tmp=node[node[y].l].x-node[node[x].l].x;
		for(int i=1;i<=len1;++i)tmp+=node[node[bitr[i]].l].x;
		for(int i=1;i<=len2;++i)tmp-=node[node[bitl[i]].l].x;
		if(tmp>=size)
		{
			for(int i=1;i<=len1;++i)bitr[i]=node[bitr[i]].l;
			for(int i=1;i<=len2;++i)bitl[i]=node[bitl[i]].l;
			return query(l,m,node[x].l,node[y].l,size,len1,len2);
		}
		else
		{
			for(int i=1;i<=len1;++i)bitr[i]=node[bitr[i]].r;
			for(int i=1;i<=len2;++i)bitl[i]=node[bitl[i]].r;
			return query(m+1,r,node[x].r,node[y].r,size-tmp,len1,len2);
		}
	}
public:
	void init()
	{
		cnt=0;
		memset(root1,0,sizeof(root1));
		memset(root,0,sizeof(root));
		for(int i=1;i<=n;++i)
		  insert(1,top,root1[i],root1[i-1],find(a[i]),1);
	}
	
	void change(int tar,int num)
	{
		int r=find(num),l=find(a[tar]);
		a[tar]=num;
		while(tar<=n)
		{
			insert(1,top,root[tar],0,r,1);
			insert(1,top,root[tar],0,l,-1);
			tar+=lowbit(tar);
		}
	}
	
	int getkth(int l,int r,int x)
	{
		int len1=0,len2=0;
		int ll=l-1,rr=r;
		while(rr)bitr[++len1]=root[rr],rr-=lowbit(rr);//用两个数组存储查找时需要用到的主席树的编号
		while(ll)bitl[++len2]=root[ll],ll-=lowbit(ll);
		return query(1,top,root1[l-1],root1[r],x,len1,len2);
	}
}cmt;

int main()
{
	int T;
	read(T);
	while(T--)
	{
		int m;
		read(n),read(m);
		for(R int i=1;i<=n;++i)
		  read(a[i]),X[i]=a[i];//离散化
		for(R int i=1;i<=m;++i)
		{
			readc(ask[i].ch);
			if(ask[i].ch=='Q')
			{
				read(ask[i].t1),read(ask[i].t2),read(ask[i].t3);
				X[i+n]=inf;
			}
			else
			{
				read(ask[i].t1),read(ask[i].t2);
				X[i+n]=ask[i].t2;
			}
		}
		sort(X+1,X+1+n+m);
		X[0]=-inf;top=0;
		for(R int i=1;i<=n+m;++i)
		  if(X[i]!=X[i-1])X[++top]=X[i];
		cmt.init();
		for(R int i=1;i<=m;++i)
		{
			if(ask[i].ch=='Q')
			  printf("%d\n",X[cmt.getkth(ask[i].t1,ask[i].t2,ask[i].t3)]);
			else
			  cmt.change(ask[i].t1,ask[i].t2);
		}
	}
	return 0;
}

最后祝你：身体健康。再见。