常用算法模板
数论
组合数
方法1(小数据)
数据范围
\(1 \leq n \leq 10000\),\(1 \leq b \leq a \leq 2000\)
说明
通过递推预处理组合数
公式
\(C^{b}_{a} = C^{b}_{a - 1} + C^{b - 1}_{a - 1}\)
LL C[N][N];
void init() {
for (int i = 0; i < N; i ++ ) {
for (int j = 0; j <= i; j ++ ) {
if (!j) C[i][j] = 1;
else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % MOD;
}
}
}
方法2(小于1e5)
数据范围
\(1 \leq n \leq 10000\),\(1 \leq b \leq a \leq 1e5\)
说明
初始化数据和数据得逆元,通过组合数公式求解
公式
\(C^{b}_{a} = \frac{a!}{b! (a - b)!}\)
LL fact[N], infact[N];
void init() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ ) {
fact[i] = fact[i - 1] * i % MOD;
infact[i] = ksm(fact[i], MOD - 2) % MOD; // 需要快速幂
}
}
LL C(int a, int b) {
if (b > a) return 0;
return fact[a] * infact[b] % MOD * infact[a - b] % MOD;
}
方法3 (小数据大范围)
数据范围
\(1 \leq n \leq 20\) \(1 \leq b \leq a \leq 1e18\)
说明
通过卢卡斯定理控制 \(a, b\) 的范围,满足条件后使用公式计算
公式
把\(a,b\) 看作 \(p\) 进制数来计算 \(C_a^b\equiv C_{a\%p}^{b\%p} \times C_{a/p}^{b/p}(MODp)\)
LL C(LL a, LL b) {
if (b > a) return 0;
LL res = 1;
for (LL i = 1, j = a; i <= b; i ++ , j -- ) {
res = (res * j % MOD * ksm(i, MOD - 2) % MOD);
}
return res;
}
LL lucas(LL a,LL b) {
if(a < MOD && b < MOD) return C(a,b);
else return C(a % MOD, b % MOD) * lucas(a / MOD, b / MOD) % MOD;
}
方法4 (高精)
数据范围
\(1 \le b\le a\le 5000\)
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n) { //记得调用 get_primes(max(a, b));
st[0] = st[1] = true; //特判1,和0不是质数。
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ ) { // n/i防止爆int
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p) {
int res = 0;
while (n) {
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b) {
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ ) {
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t) {
c.push_back(t % 10);
t /= 10;
}
return c;
}
void C(int a, int b) {
for (int i = 0; i < cnt; i ++ ) {
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; i -- ) cout << res[i];
cout << endl;
}
质数
性质
\(1\sim n\) 中至多有 \(\frac{n}{\ln n}\) 个质数
试除法判质数
bool is_prime(int n) {
if (n < 2) return false;
for (int i = 2; i <= n / i; i ++ )
if (n % i == 0)
return false;
return true;
}
分解质因数
由算术基本定理,一个整数\(N\)可分解成:\(N = p_1^{a_1}p_2^{a_2}...p_k^{a_k}\)
#include <iostream>
#include <algorithm>
using namespace std;
void divide(int x) {
for (int i = 2; i <= x / i; i ++ ) //i <= x / i:防止越界,速度大于 i < sqrt(x)
if (x % i == 0) { //i为底数
int s = 0; //s为指数
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl; //输出
}
if (x > 1) cout << x << ' ' << 1 << endl; //如果x还有剩余,单独处理
cout << endl;
}
int main() {
int n;
cin >> n;
while (n -- ) {
int x;
cin >> x;
divide(x);
}
return 0;
}
埃氏筛法
时间复杂度
\(O(nloglogn)\)
说明
遍历所有质数的倍数,剩余未被标记的数便是质数
LL primes[N], cnt;
bool st[N];
void get_primes(int n) {
st[0] = st[1] = true;
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) {
primes[cnt ++ ] = i;
for (int j = i * 2; j <= n; j += i) {
st[j] = true;
}
}
}
}
线性筛法
时间复杂度
\(O(n)\)
说明
通过提前退出来减少时间复杂度
LL primes[N], cnt;
bool st[N];
void get_primes(int n) {
st[0] = st[1] = true; //特判1,和0不是质数。
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ ) { // n/i防止爆int
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
约数
约数个数
一个数的约数个数大概是\(log(n)\)个,公约数同理
原理
设\(N=p_1^{a_1}\times p_2^{a_2}\times ...\times p_k^{a_k}\) (\(p\)为质因子)
对于任意约数 \(d=p_1^{b_1}\times p_2^{b_2}...\times p_k^{b_k} (0\le b_i \le a_i)\)
所以约数的个数 \(ans=\prod_{i = 1}^{k} a_i+1 = (a_1 + 1)+(a_2+1)+...+(a_k+1)\)
LL approximate_count(LL n) {
unordered_map<LL, LL> primes;
for (LL i = 2; i <= n / i; i ++ ) {
while (n % i == 0) {
n /= i;
primes[i] ++ ;
}
}
if (n > 1) primes[n] ++ ;
LL res = 1;
for (auto &[p, a] : primes) res = res * (a + 1) % MOD; //需定义MOD
return res;
}
约数之和
原理
\(ans=\prod_{i=1}^k\sum_{j=0}^{a_i} p_i^j=(p_1^0+p_1^1+...+p_1^{a_1})\times(p_2^0+p_2^1+...+p_2^{a_2})\times...\times(p_k^0+p_k^1+...+p_k^{a_k})\)
LL approximate_sum(LL n) {
unordered_map<LL, LL> primes;
for (LL i = 2; i <= n / i; i ++ ) {
while (n % i == 0) {
n /= i;
primes[i] ++ ;
}
}
if (n > 1) primes[n] ++ ;
LL res = 1;
for (auto &[p, a] : primes) {
LL t = 1;
while (a -- ) t = (t * p + 1) % MOD; //需定义MOD
res = res * t % MOD;
}
return res;
}
辗转相减法
说明
\(a = c^x\),\(b = c^y\) ,\(sub\_gcd(a, b) = c^{gcd(x,y)}\)
LL sub_gcd(LL a, LL b) {
if (a < b) return sub_gcd(b, a);
return b == 1 ? a : sub_gcd(b, a / b);
}
欧几里得算法
说明
计算 \(a\) 和 \(b\) 的最大公约数
LL gcd(LL a, LL b) {
return b ? gcd(b, a % b) : a;
}
扩展欧几里得算法
说明
求出一对 \(x\) , \(y\) 使其满足 \(a\times x + b \times y = gcd(a, b)\)
LL exgcd(LL a, LL b, LL &x, LL &y) { //引用来传递x, y的值, 返回值为gcd(a, b)
if (!b) {
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y = y - a / b * x;
return d;
}
欧拉函数
性质
\(1\) ~ \(N\) 中互质的数的个数被称为欧拉函数,记为 \(\phi(N)\)。
朴素求欧拉函数
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0) { //找到质因子
res = res / i * (i - 1); // 先除后乘
while (x % i == 0) x /= i; // 对 n 进行约分
}
if (x > 1) res = res / x * (x - 1); // 如果有剩余,则剩余是个质因子
return res;
}
筛法求欧拉函数
int primes[N], cnt;
int euler[N];
bool st[N];
void get_eulers(int n) {
euler[1] = 1;
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) {
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ ) {
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0) {
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
位运算
通用技巧
-
求 \(n\) 的第 \(k\) 位数字:
n >> k & 1 -
返回 \(n\) 的最后一位 \(1\) 二进制形式为 \(1\) 后面跟着一堆 \(0\)
LL lowbit(LL x) { return x & -x; } -
去掉 \(n\) 的最后一位 \(1\):
k & (k - 1)
快速幂
时间复杂度
\(O(logn)\)
说明
将乘方转化为乘法进行计算
LL ksm(LL a, LL n) { //计算 a ^ n % MOD;
LL res = 1;
while (n) {
if (n & 1) res = res * a % MOD;
a = a * a % MOD;
n >>= 1;
}
return res;
}
龟速乘
时间复杂度
\(O(logn)\)
说明
将乘法转化为加法进行计算
LL ksc(LL a, LL n) { //计算a * n % MOD;
LL res = 0;
while (n) {
if (n & 1) res = (res + a) % MOD;
a = (a + a) % MOD;
n >>= 1;
}
return res;
}
线性同余方程
\(a \ast x \equiv b \ (\text{mod} \ m)\),在有解时,先用欧几里得算法求出一组整数 \(x_0, y_0\),满足\(a \ast x_0 + m \ast y_0 = \gcd(a, m)\)
然后 \(x = x_0 \ast \dfrac{b}{\gcd(a, m)}\) 就是原线性同余方程的一个解。
给定 \(n\) 组数据 \(a_i,b_i,m_i\),对于每组数求出一个 \(x_i\),使其满足 \(a_i×x_i≡b_i(modm_i)\),如果无解则输出 impossible。
输入格式
第一行包含整数 \(n\)。
接下来 \(n\) 行,每行包含一组数据 \(a_i,b_i,m_i\)。
输出格式
输出共 \(n\) 行,每组数据输出一个整数表示一个满足条件的 \(x_i\),如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 \(int\) 范围之内。
输入样例
2
2 3 6
4 3 5
输出样例
impossible
-3
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
// a * x ≡ b (mod m)
// 变形为拓展欧几里得形式:a * x + b * y = gcd(a, b)
// 原式变为: a * x = m * y + b (注:mod m 为 b, 则相当于结果为 m 的倍数和 b 的和)
// a * x - m * y = b
// 另y1 = -y得:a * x + m * y1 = b
// 根据拓展欧几里得定理,只要 b 是 gcd(a, m)的倍数即有解!
// 另d = gcd(a, m), 我们得到的式子其实是:a * x + m * y1 = gcd(a, m) = d (注;上面的b其实就是d的倍数)
// 所以左右同乘 b / d 即可转化为:a * x * b / d + m * y1 * b / d = b * b / d = b
int exgcd(int a, int b, int &x, int &y) {
if (!b) {
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main() {
int n;
scanf("%d", &n);
while (n -- ) {
int a, b, m;
scanf("%d%d%d", &a, &b, &m);
int x, y;
int d = exgcd(a, m, x, y);
if (b % d) puts("impossible");
else printf("%d\n", (LL)b / d * x % m);
}
return 0;
}
中国剩余定理
设 \(m_1, m_2, \cdots, m_n\) 是两两互质的整数,\(m = \prod_{i=1}^{n} m_i\),\(M_i = \dfrac{m}{m_i}\),\(t_i\) 是线性同余方程
\[M_i t_i \equiv 1 \ (\text{mod} \ m_i) \]的一个解。对于任意的 \(n\) 个整数 \(a_1, a_2, \cdots, a_n\),方程组
\[\begin{cases} x \equiv a_1 \ (\text{mod} \ m_1) \\ x \equiv a_2 \ (\text{mod} \ m_2) \\ \cdots \\ x \equiv a_n \ (\text{mod} \ m_n) \end{cases} \]有整数解,解为
\[x = \sum_{i=1}^{n} a_i M_i t_i \]给定\(2n\)个整数 \(a_1,a_2,...,a_n\) 和 \(m_1,m_2,...,m_n\),求一个最小的非负整数 \(x\),满足 \(\forall i \in [1, n], x \equiv m_i \ (\text{mod} \ a_i)\)。
输入格式
第 \(1\) 行包含整数 \(n\)。
第 \(2…n+1\) 行:每 \(i+1\) 行包含两个整数 \(a_i\) 和 \(m_i\),数之间用空格隔开。
输出格式
输出最小非负整数 \(x\),如果 \(x\) 不存在,则输出 \(−1\)。
输入样例
2
8 7
11 9
输出样例
31
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y){
if (!b) {
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main() {
int n;
cin >> n;
LL x = 0, m1, a1;
cin >> a1 >> m1;
for (int i = 0; i < n - 1; i ++ ){
LL m2, a2;
cin >> a2 >> m2;
LL k1, k2;
LL d = exgcd(a1, a2, k1, k2);
if ((m2 - m1) % d) {
x = -1;
break;
}
//更新状态
k1 *= (m2 - m1) / d;
LL t = a2 / d;
//将解变成一个最小的正整数解
k1 = (k1 % t + t) % t;
x = k1 * a1 + m1;
//更新a和m,k只是个变量,不用管,取余的时候会自动消失
m1 = k1 * a1 + m1;
a1 = abs(a1 / d * a2);
}
if (x != -1) x = (m1 % a1 + a1) % a1;
cout << x << endl;
return 0;
}
BSGS
解决高次同余方程
给定正整数 \(a,p,b\) 数据保证 \(a\) 和 \(p\) 互质。
求满足 \(a^x ≡ b(mod\ p)\) 的最小非负整数 \(x\) 。
输入格式
每个测试文件中最多包含 \(100\) 组测试数据。
每组数据中,每行包含 \(3\) 个正整数 \(a,p,b\)。
当 \(a=p=b=0\) 时,表示测试数据读入完全。
输出格式
对于每组数据,输出一行。
如果有 \(x\) 满足该要求,输出最小的非负整数 \(x\),否则输出 No Solution。
输入样例
3 5 2
3 2 1
0 0 0
输出样例
3
0
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <unordered_map>
using namespace std;
typedef long long LL;
int bsgs(int a, int b, int p) { //bsgs 算法求高次同余方程的最小正整数解
if (1 % p == b % p) return 0; //特判 0
int k = sqrt(p) + 1;
unordered_map<int, int> hash; //哈希表存储所有 b * a^y (mod p) 的值
for (int i = 0, j = b % p; i < k; i ++ ) { //枚举所有 y,将所有可能的值存下来
hash[j] = i;
j = (LL)j * a % p;
}
int ak = 1; //记录 a^k
for (int i = 0; i < k; i ++ ) ak = (LL)ak * a % p; //求 a^k
for (int i = 1, j = ak; i <= k; i ++ ) { //i 枚举 x,j 表示 ak^x
if (hash.count(j)) return (LL)i * k - hash[j]; //如果当前的 x 满足条件,说明找到最小正整数解,直接返回 k * x - y
j = (LL)j * ak % p; //继续往下枚举
}
return -1; //到此说明无解,返回 -1
}
int main() {
int a, p, b;
while (cin >> a >> p >> b, a || p || b) {
int res = bsgs(a, b, p);
if (res == -1) puts("No Solution");
else cout << res << endl;
}
return 0;
}
扩展BSGO
当 \(a,p\) 不互质时的做法
给定正整数 \(a,p,b\)
求满足 \(a^x ≡ b(mod\ p)\) 的最小非负整数 \(x\) 。
输入格式
每个测试文件中最多包含 \(100\) 组测试数据。
每组数据中,每行包含 \(3\) 个正整数 \(a,p,b\)。
当 \(a=p=b=0\) 时,表示测试数据读入完全。
输出格式
对于每组数据,输出一行。
如果有 \(x\) 满足该要求,输出最小的非负整数 \(x\),否则输出 No Solution。
输入样例
5 58 33
2 4 3
0 0 0
输出样例
9
No Solution
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int INF = 1e8;
int exgcd(int a, int b, int& x, int& y) { //扩展欧几里得算法
if (!b) {
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int bsgs(int a, int b, int p) { //BSGS 算法
if (1 % p == b % p) return 0; //特判 0
int k = sqrt(p) + 1;
unordered_map<int, int> hash; //存储所有 b * a^y 的值
for (int i = 0, j = b % p; i < k; i ++ ) { //i 表示 y,j 表示 b * a^y
hash[j] = i; //记录所有 b * a^y 对应的 y(y 尽可能大)
j = (LL)j * a % p;
}
int ak = 1; //记录 a^k
for (int i = 0; i < k; i ++ ) ak = (LL)ak * a % p;
for (int i = 1, j = ak; i <= k; i ++ ) { //i 表示 x,j 表示 ak^x
if (hash.count(j)) return i * k - hash[j]; //如果找到一组 x, y 满足方程,说明有解
j = (LL)j * ak % p;
}
return -INF; //否则说明无解
}
int exbsgs(int a, int b, int p) { //扩展 BSGS 算法
b = (b % p + p) % p; //保证 b 是非负数
if (1 % p == b % p) return 0; //特判 0
int x, y;
int d = exgcd(a, p, x, y); //求 a 和 p 的最大公约数
if (d > 1) { //如果 a 和 p 不互质,则需要处理
if (b % d) return -INF; //如果 b 不能整除 d,说明无解
exgcd(a / d, p / d, x, y); //线性同余方程求 a / d 的逆元 x
return exbsgs(a, (LL)b / d * x % (p / d), p / d) + 1; //递归处理
}
return bsgs(a, b, p); //如果 a 和 p 互质,直接用普通 BSGS 求
}
int main() {
int a, p, b;
while (cin >> a >> p >> b, a || p || b) {
int res = exbsgs(a, b, p);
if (res < 0) puts("No Solution");
else cout << res << endl;
}
return 0;
}
Catalan数
给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\),它们将按照某种顺序排成长度为 \(2n\) 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个。
输出的答案对 \(10^9+7\) 取模。
输入格式
共一行,包含整数 \(n\)。
输出格式
共一行,包含一个整数,表示答案。
输入样例
3
输出样例
5
说明
重要公式
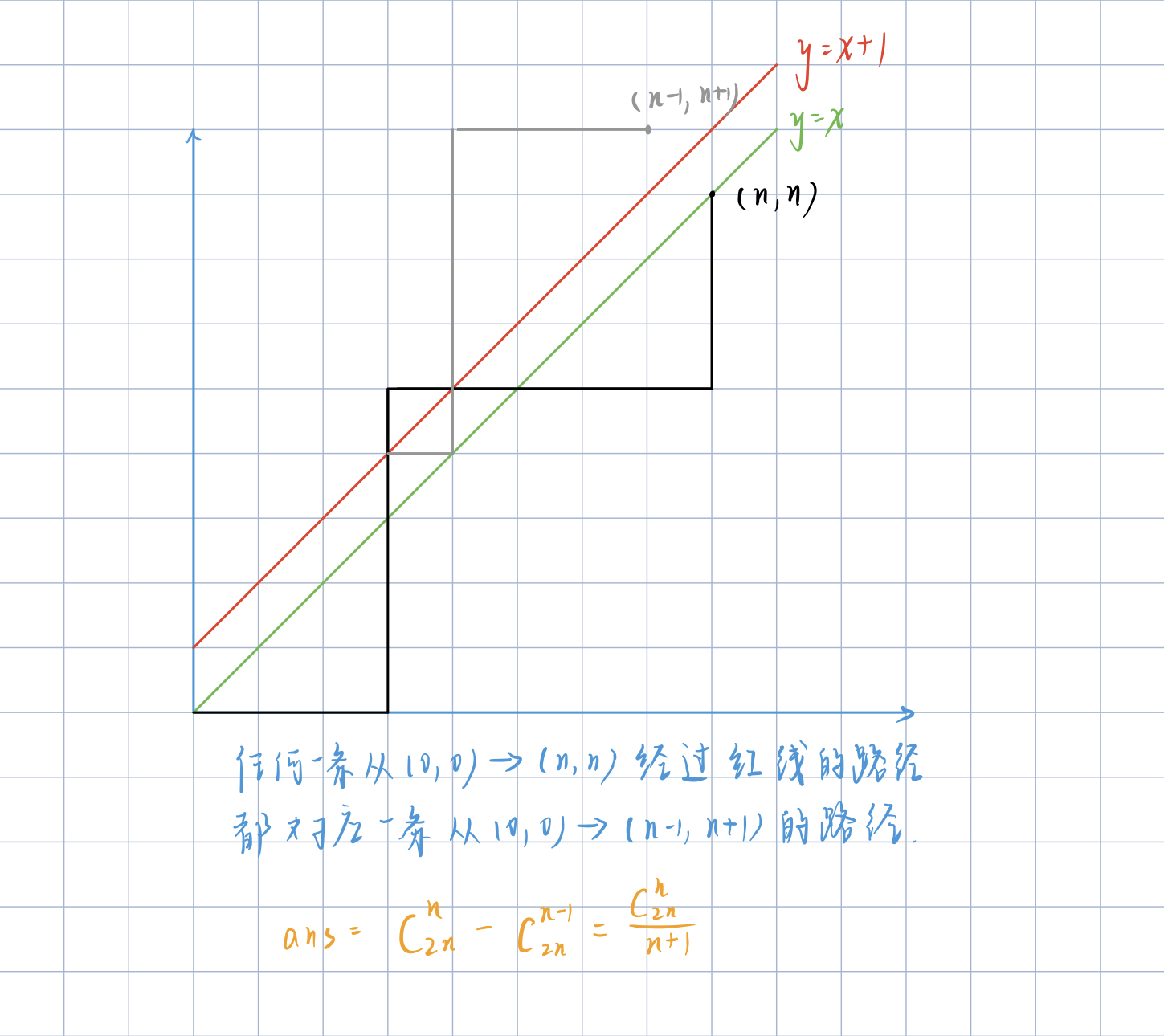
\(res = C_{2n}^{n} - C_{2n-1}^{n-1} = \frac{C_{2n}^{n}}{n+1}\)
- \(C_{2n}^{n}\):从 \((1, 1)\) 到 \((n, n)\) 的路线总数
- \(C_{2n-1}^{n-1}\):从 \((1, 1)\) 到 \((n-1, n+1)\) 经过直线 \(y = x + 1\),故可以关于此直线对称得到一条从 \((1, 1)\) 到 \((n, n)\) 的不合法路线,即从 \((1, 1)\) 到 \((n-1, n+1)\) 的每一条路线都对应一条从 \((1, 1)\) 到 \((n, n)\) 的不合法路线。
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MOD = 1e9 + 7;
int ksm(int x, int n) {
int res = 1;
while (n) {
if (n & 1) res = (LL)res * x % MOD;
x = (LL)x * x % MOD;
n >>= 1;
}
return res;
}
int main() {
int n;
cin >> n;
int a = 2 * n, b = n;
int res = 1;
for (int i = a; i > a - b; i -- ) res = (LL)res * i % MOD;
for (int i = 1; i <= b; i ++ ) res = (LL)res * ksm(i, MOD - 2) % MOD;
res = (LL)res * ksm(n + 1, MOD - 2) % MOD;
cout << res;
return 0;
}
第一类Stirling数(斯特林轮换数)


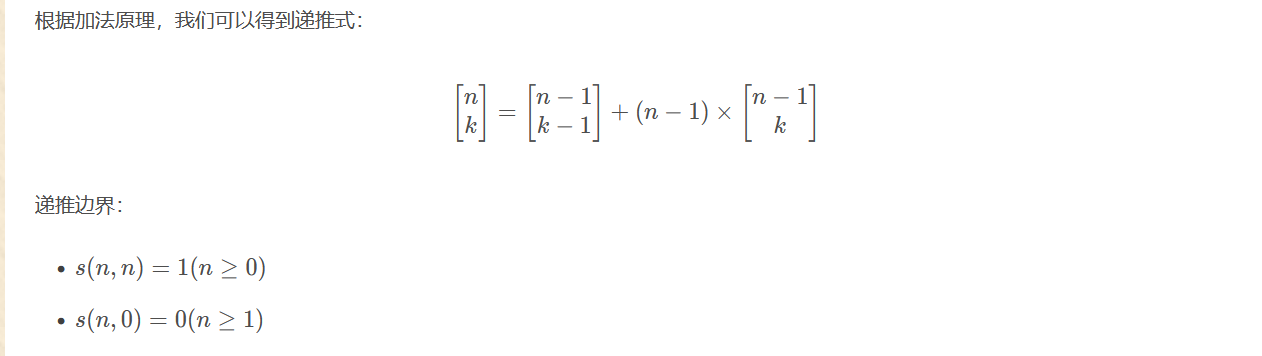

将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空圆排列的方案数:
\[\left[ \begin{matrix} n \\ k \end{matrix} \right] = \left[ \begin{matrix} n-1 \\ k-1 \end{matrix} \right] + (n-1) \left[ \begin{matrix} n-1 \\ k \end{matrix} \right] \]
第一类斯特林数(斯特林轮换数) \(\left[ \begin{matrix} n \\ k \end{matrix} \right]\) 表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空圆排列的方案数。
现在,给定 \(n\) 和 \(k\),请你求方案数。
圆排列定义:圆排列是排列的一种,指从 \(n\) 个不同元素中取出 \(m\) (\(1 \leq m \leq n\)) 个不同的元素排列成一个环形,既无头也无尾。两个圆排列相同当且仅当所取元素的个数相同并且元素取法一致,在环上的排列顺序一致。
输入格式
两个整数 \(n\) 和 \(k\)。
输出格式
输出一个整数表示划分方案数。
答案对 \(10^9+7\) 取模。
输入样例
3 2
输出样例
3
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1010, MOD = 1e9 + 7;
int n, m;
int f[N][N];
int main() {
cin >> n >> m;
f[0][0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
f[i][j] = (f[i - 1][j - 1] + (LL)(i - 1) * f[i - 1][j]) % MOD;
cout << f[n][m] << endl;
return 0;
}
第二类Stirling数(斯特林子集数)
将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空子集的方案数:
\[\left\{ \begin{matrix} n \\ k \end{matrix} \right\} = \left\{ \begin{matrix} n-1 \\ k-1 \end{matrix} \right\} + k \left\{ \begin{matrix} n-1 \\ k \end{matrix} \right\} \]
第二类斯特林数(斯特林子集数) \(\left\{ \begin{matrix} n \\ k \end{matrix} \right\}\) 表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个非空子集的方案数。
现在,给定 \(n\) 和 \(k\),请你求方案数。
输入格式
两个整数 \(n\) 和 \(k\)。
输出格式
输出一个整数表示划分方案数。
答案对 \(10^9+7\) 取模。
输入样例
3 2
输出样例
3
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1010, MOD = 1e9 + 7;
int n, m;
int f[N][N];
int main() {
cin >> n >> m;
f[0][0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
f[i][j] = (f[i - 1][j - 1] + (LL)(i - 1) * f[i - 1][j]) % MOD;
cout << f[n][m] << endl;
return 0;
}
高斯消元
输入一个包含 \(n\) 个方程 \(n\) 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 \(m\) 个方程 \(n\) 个未知数的线性方程组示例:
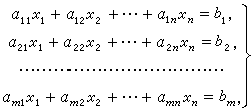
输入格式
第一行包含整数 \(n\)。
接下来 \(n\) 行,每行包含 \(n+1\) 个实数,表示一个方程的 \(n\) 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 \(n\) 行,其中第 \(i\) 行输出第 \(i\) 个未知数的解,结果保留两位小数。
注意:本题有 SPJ,当输出结果为 0.00 时,输出 -0.00 也会判对。在数学中,一般没有正零或负零的概念,所以严格来说应当输出 0.00,但是考虑到本题作为一道模板题,考察点并不在于此,在此处卡住大多同学的代码没有太大意义,故增加 SPJ,对输出 -0.00 的代码也予以判对。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
输入样例
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例
1.00
-2.00
3.00
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
const double eps = 1e-8;
int n;
double a[N][N];
int gauss() { // 高斯消元,答案存于a[i][n]中,0 <= i < n
int c, r;
for (c = 0, r = 0; c < n; c ++ ) {
int t = r;
for (int i = r; i < n; i ++ ) // 找绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端
for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1
for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j -- )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n) {
for (int i = r; i < n; i ++ )
if (fabs(a[i][n]) > eps)
return 2; // 无解
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n + 1; j ++ )
scanf("%lf", &a[i][j]);
int t = gauss();
if (t == 2) puts("No solution");
else if (t == 1) puts("Infinite group solutions");
else {
for (int i = 0; i < n; i ++ )
printf("%.2lf\n", a[i][n]);
}
return 0;
}
Nim博弈
Nim博弈先手必胜,当且仅当 \(A_1 \ xor \ A_2 \ xor \ \cdots \ xor \ A_n \neq 0\)。
给定 \(n\) 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 \(n\)。
第二行包含 \(n\) 个数字,其中第 \(i\) 个数字表示第 \(i\) 堆石子的数量。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
输入样例
2
2 3
输出样例
Yes
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int main() {
int n;
scanf("%d", &n);
int res = 0;
while (n -- ) {
int x;
scanf("%d", &x);
res ^= x;
}
if (res) puts("Yes");
else puts("No");
return 0;
}
莫比乌斯反演



若 \(F(n) = \sum_{d \mid n} (d)\),则 \(f(n) = \sum_{d \mid n} \mu(d) F\left(\frac{n}{d}\right)\)
对于给出的 \(n\) 个询问,每次求有多少个数对 \((x, y)\),满足 \(a \leq x \leq b\),\(c \leq y \leq d\),且 \(\gcd(x, y) = k\),\(\gcd(x, y)\) 函数为 \(x\) 和 \(y\) 的最大公约数。
输入格式
第一行一个整数 \(n\)。
接下来 \(n\) 行每行五个整数,分别表示 \(a、b、c、d、k\)。
输出格式
共 \(n\) 行,每行一个整数表示满足要求的数对 \((x,y)\) 的个数。
输入样例
2
2 5 1 5 1
1 5 1 5 2
输出样例
14
3
说明

参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50010;
int primes[N], cnt, mu[N], sum[N]; //存储所有质数, 莫比乌斯函数, 莫比乌斯函数的前缀和
bool st[N]; //记录每个数是不是合数
void init() { //预处理莫比乌斯函数
//线性筛法求莫比乌斯函数
mu[1] = 1;
for (int i = 2; i < N; i ++ ) {
if (!st[i]) primes[cnt ++ ] = i, mu[i] = -1;
for (int j = 0; primes[j] * i < N; j ++ ) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
mu[primes[j] * i] = -mu[i];
}
}
for (int i = 1; i < N; i ++ ) sum[i] = sum[i - 1] + mu[i]; //预处理前缀和
}
int g(int k, int x) { //返回 x 所在区间的最后一个数
return k / (k / x);
}
LL f(int a, int b, int k) { //求 f(k),f(k) 表示在 (0,0) ~ (a,b) 的矩阵中满足 gcd(x,y) == k 的点的数量
a = a / k, b = b / k;
LL res = 0; //记录答案
int n = min(a, b);
for (int l = 1, r; l <= n; l = r + 1) { //枚举区间左端点
r = min(n, min(g(a, l), g(b, l))); //计算右端点
res += (LL)(sum[r] - sum[l - 1]) * (a / l) * (b / l); //累加答案
}
return res; //返回答案
}
int main() {
init(); //预处理
int T;
scanf("%d", &T);
while (T -- ) {
int a, b, c, d, k;
scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
printf("%lld\n", f(b, d, k) - f(a - 1, d, k) - f(b, c - 1, k) + f(a - 1, c - 1, k));
}
return 0;
}
设 \(d(x)\) 为 \(x\) 的约数个数,给定 \(N, M\),求
输入格式
输入多组测试数据。
第一行,一个整数 \(T\),表示测试数据的组数。
接下来的 \(T\) 行,每行两个整数 \(N、M\)。
输出格式
\(T\) 行,每行一个整数,表示你所求的答案。
输入样例
2
7 4
5 6
输出样例
110
121
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50010;
int primes[N], cnt, mu[N], sum[N], h[N];
bool st[N];
int g(int k, int x) { //返回x所在段的分块右端点
return k / (k / x);
}
void init() {
mu[1] = 1;
for (int i = 2; i < N; i ++ ) {
if (!st[i]) primes[cnt ++ ] = i, mu[i] = -1;
for (int j = 0; primes[j] * i < N; j ++ ) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
mu[i * primes[j]] = -mu[i];
}
}
for (int i = 1; i < N; i ++ ) sum[i] = sum[i - 1] + mu[i]; //预处理莫比乌斯函数前缀和
for (int i = 1; i < N; i ++ ) { //枚举段长
for (int l = 1, r; l <= i; l = r + 1) { //枚举点
r = min(i, g(i, l));
h[i] += (r - l + 1) * (i / l);
}
}
}
int main() {
init();
int T;
scanf("%d", &T);
while (T -- ) {
int n, m;
scanf("%d%d", &n, &m);
LL res = 0;
int k = min(n, m); //终点
for (int l = 1, r; l <= k; l = r + 1) {
r = min(k, min(g(n, l), g(m, l))); //选取最小的跳
res += (LL)(sum[r] - sum[l - 1]) * h[n / l] * h[m / l]; //公式
}
printf("%lld\n", res);
}
return 0;
}
burnside引理
每个置换的不动点个数的平均值就是不同的方案数
给定 \(M\) 种不同颜色的珠子,每种颜色的珠子的个数都足够多。
现在要从中挑选 \(N\) 个珠子,串成一个环形手链。
请问一共可以制作出多少种不同的手链。
注意,如果两个手链经旋转或翻转后能够完全重合在一起,对应位置的珠子颜色完全相同,则视为同一种手链。
输入格式
输入包含多组测试数据。
每组测试数据占一行,包含两个整数 \(M,N\)。
最后一行包含 0 0 表示输入结束。
输出格式
每组数据输出一个占一行的整数表示结果。
输入样例
1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0
输出样例
1
2
3
5
8
13
21
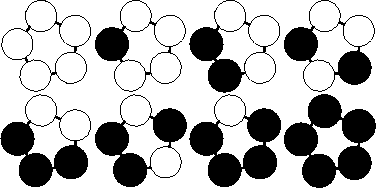
样例解释
当 \(M=2,N=5\) 时,一共可以制作出 \(8\) 种不同的手链,如下图。
说明
题意简化:给一个有\(N\)个珠子的环染色,颜色一共有\(M\)种,
旋转或翻转后能够完全重合在一起而且对应位置颜色一致为一种情况,问方案数?
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
LL power(int a, int b) {
LL res = 1;
while (b -- ) res *= a;
return res;
}
int main() {
int m, n;
while (cin >> m >> n, m || n) {
LL res = 0;
for (int i = 0; i < n; i ++ )
res += power(m, gcd(n, i));
if (n % 2)
res += n * power(m, (n + 1) / 2);
else
res += n / 2 * (power(m, n / 2 + 1) + power(m, n / 2));
cout << res / n / 2 << endl;
}
return 0;
}
Pólya定理
旋转置换一共 \(n\) 个置换,第 \(i\) 个置换的循环节的个数为 \(\gcd(n, i)\)
则:
\[\sum_{k=0}^{m} m^{(n, k)} \]旋转置换
当 \(n\) 为奇数时:\(n \ast m^{\frac{n+1}{2}}\)
当 \(n\) 为偶数时:
\[\frac{\left(n \ast m^{\frac{n}{2} + 1} + n \ast m^{\frac{n}{2}}\right)}{\frac{n}{2}} \]
给定 \(m\) 种不同颜色的魔法珠子,每种颜色的珠子的个数都足够多。
现在要从中挑选 \(n\) 个珠子,串成一个环形魔法手链。
魔法珠子之间存在 \(k\) 对排斥关系,互相排斥的两种颜色的珠子不能相邻,否则会发生爆炸。(同一种颜色的珠子之间也可能存在排斥)
请问一共可以制作出多少种不同的手链。
注意,如果两个手链经旋转后能够完全重合在一起,对应位置的珠子颜色完全相同,则视为同一种手链。
答案对 \(9973\) 取模。
输入格式
第一行包含整数 \(T\),表示共有 \(T\) 组测试数据。
每组数据第一行包含三个整数 \(n,m,k\)。
接下来 \(k\) 行,每行包含两个整数 \(a,b\),表示颜色 \(a\) 的珠子不能和颜色 \(b\) 的珠子相邻。
\(m\) 种颜色编号为 \(1∼m\)。
输出格式
每组数据输出一行一个整数,表示答案。
输入样例
4
3 2 0
3 2 1
1 2
3 2 2
1 1
1 2
3 2 3
1 1
1 2
2 2
输出样例
4
2
1
0
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 11, P = 9973;
int m;
struct Matrix {
int a[N][N];
Matrix() {
memset(a, 0, sizeof a);
}
};
Matrix operator* (Matrix a, Matrix b) {
Matrix c;
for (int i = 1; i <= m; i ++ )
for (int j = 1; j <= m; j ++ )
for (int k = 1; k <= m; k ++ )
c.a[i][j] = (c.a[i][j] + a.a[i][k] * b.a[k][j]) % P;
return c;
}
int qmi(Matrix a, int b) {
Matrix res;
// 初始化矩阵
for (int i = 1; i <= m; i ++ ) res.a[i][i] = 1;
while (b) {
if (b & 1) res = res * a;
a = a * a;
b >>= 1;
}
// 算对角线答案
int sum = 0;
for (int i = 1; i <= m; i ++ ) sum += res.a[i][i];
return sum % P;
}
int phi(int n) {
int res = n;
for (int i = 2; i * i <= n; i ++ )
if (n % i == 0) {
res = res / i * (i - 1);
while (n % i == 0) n /= i;
}
if (n > 1) res = res / n * (n - 1);
return res % P;
}
int inv(int n) {
n %= P;
for (int i = 1; i < P; i ++ )
if (i * n % P == 1)
return i;
return -1;
}
int main() {
int T;
cin >> T;
while (T -- ) {
int n, k;
cin >> n >> m >> k;
Matrix tr;
// 构造矩阵
for (int i = 1; i <= m; i ++ )
for (int j = 1; j <= m; j ++ )
tr.a[i][j] = 1;
while (k -- ) {
int x, y;
cin >> x >> y;
tr.a[x][y] = tr.a[y][x] = 0;
}
// 枚举 n 的约数算答案
int res = 0;
for (int i = 1; i * i <= n; i ++ )
if (n % i == 0) {
res = (res + qmi(tr, i) * phi(n / i)) % P;
if (i != n / i)
res = (res + qmi(tr, n / i) * phi(i)) % P;
}
// 结尾别忘除以 n
cout << res * inv(n) % P << endl;
}
return 0;
}
FFT
给定一个 \(n\) 次多项式 \(F(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n\)。
以及一个 \(m\) 次多项式 \(G(x) = b_0 + b_1 x + b_2 x^2 + \dots + b_m x^m\)。
已知 \(H(x) = F(x) \cdot G(x) = c_0 + c_1 x + c_2 x^2 + \dots + c_{n+m} x^{n+m}\)。
请你计算并输出 \(c_0, c_1, \dots, c_{n+m}\)。
输入格式
第一行包含两个整数 \(n,m\)。
第二行包含 \(n+1\) 个整数 \(a_0,a_1,…,a_n\)。
第三行包含 \(m+1\) 个整数 \(b_0,b_1,…,b_m\)。
输出格式
共一行,依次输出 \(0,c_1,…,c_{n+m}\)。
输入样例
1 2
1 3
2 2 1
输出样例
2 8 7 3
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 300010;
const double PI = acos(-1);
int n, m;
struct Complex { //复数
double x, y; //x + yi
Complex operator+ (const Complex& t) const { //复数减法
return {x + t.x, y + t.y};
}
Complex operator- (const Complex& t) const { //复数加法
return {x - t.x, y - t.y};
}
Complex operator* (const Complex& t) const { //复数乘法
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
}a[N], b[N]; //多项式的点表示法
//rev[i] 表示 i 的二进制翻转后的数,bit 表示二进制有效位数,tot 表示总长度
int rev[N], bit, tot;
//inv 为 1 表示正向变换,系数表示法 -> 点表示法
//inv 为 -1 表示逆向变换,点表示法 -> 系数表示法
void fft(Complex a[], int inv) { //快速傅里叶变换
//将序列变成最底层的顺序
for (int i = 0; i < tot; i ++ )
if (i < rev[i]) //只交换一次,否则换过去换回来顺序不变
swap(a[i], a[rev[i]]);
for (int mid = 1; mid < tot; mid <<= 1) { //当前每段区间长度为 2 * mid,下面一层的区间长度为 mid
//2 * mid 表示当前区间的长度,即当前的 n
//如果是正向变换夹角是正的,如果是逆向变换则方向相反,故夹角是负的
auto w1 = Complex({cos(PI / mid), inv * sin(PI / mid)});
for (int i = 0; i < tot; i += mid * 2) { //枚举当前每段区间的开头
auto wk = Complex({1, 0}); //k 从 0 开始枚举,w0 = (1, 0)
for (int j = 0; j < mid; j ++, wk = wk * w1) { //枚举当前区间中的每一项并计算值
//A(wk) = A1(wk) +/- wk * A2(wk)
auto x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i ++ ) scanf("%lf", &a[i].x);
for (int i = 0; i <= m; i ++ ) scanf("%lf", &b[i].x);
while ((1 << bit) < n + m + 1) bit ++; //统计有效位数
tot = 1 << bit; //统计有效位数
//预处理 rev
for (int i = 0; i < tot; i ++ )
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
fft(a, 1), fft(b, 1); //正向变换
for (int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
fft(a, -1); //逆向变换
for (int i = 0; i <= n + m; i ++ ) //将乘积的系数表示法输出
printf("%d ", (int)(a[i].x / tot + 0.5));
return 0;
}
容斥原理
给定一个整数 \(n\) 和 \(m\) 个不同的质数 \(p_1,p_2,…,p_m\)。
请你求出 \(1∼n\) 中能被 \(p_1,p_2,…,p_m\) 中的至少一个数整除的整数有多少个。
输入格式
第一行包含整数 \(n\) 和 \(m\)。
第二行包含 \(m\) 个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
输入样例
10 2
2 3
输出样例
7
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
int p[N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i ++ ) cin >> p[i];
int res = 0;
//枚举从1 到 1111...(m个1)的每一个集合状态, (至少选中一个集合)
for (int i = 1; i < 1 << m; i ++ ) {
int t = 1, s = 0; //选中集合对应质数的乘积,选中的集合数量
for (int j = 0; j < m; j ++ ) //枚举当前状态的每一位
if (i >> j & 1) { //选中一个集合
if ((LL)t * p[j] > n) { //乘积大于n, 则n/t = 0, 跳出这轮循环
t = -1;
break;
}
t *= p[j];
s ++ ; //有一个1,集合数量+1
}
if (t != -1) {
if (s % 2) res += n / t; //选中奇数个集合, 则系数应该是1, n/t为当前这种状态的集合数量
else res -= n / t; //反之则为 -1
}
}
cout << res << endl;
return 0;
}
概率与数学期望
给出一个有向无环的连通图,起点为 \(1\),终点为 \(N\),每条边都有一个长度。
数据保证从起点出发能够到达图中所有的点,图中所有的点也都能够到达终点。
绿豆蛙从起点出发,走向终点。
到达每一个顶点时,如果有 \(K\) 条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走向每条路的概率为 \(1/K\)。
现在绿豆蛙想知道,从起点走到终点所经过的路径总长度的期望是多少?
输入格式
第一行: 两个整数 \(N,M\),代表图中有 \(N\) 个点、\(M\) 条边。
第二行到第 \(1+M\) 行: 每行 \(3\) 个整数 \(a,b,c\),代表从 \(a\) 到 \(b\) 有一条长度为 \(c\) 的有向边。
输出格式
输出从起点到终点路径总长度的期望值,结果四舍五入保留两位小数。
输入样例
4 4
1 2 1
1 3 2
2 3 3
3 4 4
输出样例
7.00
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dout[N];
double f[N];
void add(int a, int b, int c) { // 建边
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
double dp(int u) {
if (f[u] >= 0) return f[u];
f[u] = 0;
for (int i = h[u]; ~i; i = ne[i]) { //求概率
int j = e[i];
f[u] += (w[i] + dp(j)) / dout[u];
}
return f[u];
}
int main() {
memset(h, -1, sizeof h);
memset(f, -1, sizeof f);
cin >> n >> m;
while (m -- ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
dout[a] ++ ;
}
printf("%.2lf", dp(1));
return 0;
}
矩阵乘法
大家都知道斐波那契数列吧,\(f_1=1,f_2=1,f_3=2,f_4=3,…,f_n=f_{n−1}+f_{n−2}\)。
现在问题很简单,输入 \(n\) 和 \(m\),求 \(f_n\) 的前 \(n\) 项和 \(S_n\ mod\ m\)。
输入格式
共一行,包含两个整数 \(n\) 和 \(m\)。
输出格式
输出前 \(n\) 项和 \(S_n\ mod\ m\) 的值。
输入样例
5 1000
输出样例
12
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3;
int n, m;
LL A[N][N] = { // 上述矩阵 A
{2, 0, -1},
{1, 0, 0},
{0, 1, 0}
};
LL S[N] = {2, 1, 0}; // 上述矩阵 S(转置)
void multi(LL A[], LL B[][N]) { // 计算方阵 B 乘向量 A,并将结果储存在 A 中
LL ans[N] = {0};
for (int i = 0; i < N; i ++ )
for (int j = 0; j < N; j ++ )
ans[i] += A[j] * B[i][j] % m;
for (int i = 0; i < N; i ++ )
A[i] = ans[i] % m;
}
void multi(LL A[][N], LL B[][N]) { // 计算方阵 A * B,并将结果储存在 A 中
LL ans[N][N] = {0};
for (int i = 0; i < N; i ++ )
for (int j = 0; j < N; j ++ )
for (int k = 0; k < N; k ++ )
ans[i][j] += A[i][k] * B[k][j] % m;
for (int i = 0; i < N; i ++ )
for (int j = 0; j < N; j ++ )
A[i][j] = ans[i][j] % m;
}
int main() {
scanf("%d%d", &n, &m);
while (n) { // 矩阵快速幂
if (n & 1) multi(S, A);
multi(A, A);
n >>= 1;
}
printf("%lld", (S[2] % m + m) % m);
return 0;
}
积性函数
龙哥现在有一道题,要考考大家。
给定一个整数 \(N\),请你求出 \(\sum_{1 \leq i \leq N} \gcd(i, N)\) 的值。
输入格式
一个整数 \(N\)。
输出格式
一个整数表示结果。
输入样例
6
输出样例
15
参考代码
#include <bits/stdc.h>
using namespace std;
typedef long long LL;
int main() {
int n;
cin >> n;
LL res = n;
for (int i = 2; i <= n / i; i ++ )
if (n % i == 0) {
int a = 0, p = i;
while (n % p == 0) a ++, n /= p;
res = res * (p + (LL)a * p - a) / p;
}
if (n > 1) res = res * ((LL)n + n - 1) / n;
cout << res << endl;
return 0;
}
生成函数
明明这次又要出去旅游了,和上次不同的是,他这次要去宇宙探险!
我们暂且不讨论他有多少经费,他又幻想了他应该带一些什么东西。
理所当然的,你当然要帮他计算带 \(N\) 件物品的方案数。
他这次准备带一些喜欢吃的食物,如:薯条多啦、鸡块啦、承德汉堡等等。
当然,他又有一些稀奇古怪的限制,每种食物的限制如下:
- 承德汉堡:偶数个。
- 可乐:\(0\)个或\(1\)个。
- 鸡腿:\(0\)个、\(1\)个或\(2\)个。
- 蜜桃多:奇数个。
- 鸡块:\(4\)的倍数个。
- 包子:\(0\)个、\(1\)个、\(2\)个或\(3\)个。
- 土豆片炒肉:不超过一个。
- 面包:\(3\)的倍数个。
注意,明明懒得考虑到底对于带的食物该怎么搭配着吃,也认为每种食物都是以“个”为单位(反正是幻想嘛),只要总数加起来是 \(N\) 就算一种方案。
因此,对于给出的 \(N\),你需要计算出方案数,并对 \(10007\) 取模。
输入格式
一个整数 \(N\)。
输出格式
一个整数,表示方案数对 \(10007\) 取模后的结果。
输入样例
5
输出样例
35
说明

参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 510, P = 10007;
char s[N];
int main() {
scanf("%s", s);
LL n = 0;
for (int i = 0; s[i]; i ++ )
n = (n * 10 + s[i] - '0') % P;
cout << n * (n + 1) * (n + 2) / 6 % P << endl;
return 0;
}
线性基
给定 \(n\) 个整数(可能重复),现在需要从中挑选任意个整数,使得选出整数的异或和最大。
请问,这个异或和的最大可能值是多少。
输入格式
第一行一个整数 \(n\)。
第二行包含 \(n\) 个整数。
输出格式
输出一个整数,表示所选整数的异或和的最大可能值。
输入样例
3
5 2 8
输出样例
15
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL p[N]; // p[i] 是出现 1 的最高位在第 i 位的数
int n;
void add(LL x) {
for (int i = 62; i >= 0; i--)
if (x & (1ll << i))
if (!p[i]) { //若线性基的第i位为0,则直接在该位插入x
p[i] = x;
return;
}
else //重复,直到
x ^= p[i];
//如果退出时x = 0,则此时线性基已经可以表示原先的x了;反之,则说明为了表示x,往线性基中加入了一个新元素
}
LL qmax() {
LL res = 0;
for (int i = 62; i >= 0; i--)
res = max(res, res ^ p[i]);
return res;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
LL x;
scanf("%lld", &x);
add(x);
}
printf("%lld\n", qmax());
return 0;
}
阶乘
- \(n! = n*(n-1)*(n-2)*...*(1)\)
- \(n!=\frac{n(n+1)(2n+1)}{6}\)
回文数
1位回文数: 9个
2位回文数: 9个
3位回文数: 90个
4位回文数: 90个
5位回文数: 900个
6位回文数: 900个
计算几何
前置知识
pi = acos(-1)- 余弦定理:\(c^2=a^2+b^2-2abcos\theta\)
- 正弦定理:\(\frac{A}{\sin a}=\frac{B}{\sin B}=\frac{C}{\sin C}=2R\)
浮点数比较
const double eps = 1e-8;
int sign(double x) { // 符号函数
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int cmp(double x, double y) { // 比较函数
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
定义
struct Point{
double x, y;
Point(double X = 0, double Y = 0) {
x = X, y = Y;
}
};
const double eps = 1e-8;
int dcmp(double a) { //处理精度
return a < -eps ? -1 : (a > eps ? 1 : 0);
}
double Abs(double a) { //取绝对值
return a * dcmp(a);
}
模长
对于 \(\vec{a} = (x, y)\),\(|\vec{a}| = \sqrt{x^2 + y^2} = \sqrt{|\vec{a}|^2}\)
double Len(Point a) { //模长
return sqrt(a.x * a.x + a.y + a.y);
}
向量加减
对于 \(\vec{a} = (x_1, y_1)\), \(\vec{b} = (x_2, y_2)\), \(\vec{a} + \vec{b} = (x_1 + x_2, y_1 + y_2)\)
对于 \(\vec{a} = (x_1, y_1)\), \(\vec{b} = (x_2, y_2)\), \(\vec{a} - \vec{b} = (x_1 - x_2, y_1 - y_2)\)
Point operator+ (Point a,Point b) {
return Point(a.x + b.x, a.y + b.y);
}
Point operator- (Point a, Point b) {
return Point(a.x - b.x, a.y - b.y);
}
向量数乘
对于 \(\vec{a} = (x, y)\),\(\lambda \vec{a} = (\lambda x, \lambda y)\)
除法也可以理解为数乘:\(\frac{\vec{a}}{\lambda} = \left( \frac{1}{\lambda} x, \frac{1}{\lambda} y \right)\)
Point operator* (Point a, double b) {
return Point(a.x * b, a.y * b);
}
点积
\(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos\theta (\theta = \langle \vec{a}, \vec{b} \rangle)\)
对于 \(\vec{a} = (x_1, y_1)\),\(\vec{b} = (x_2, y_2)\),\(\vec{a} \cdot \vec{b} = x_1 x_2 + y_1 y_2\)
夹角 \(\theta\) 与点积大小的关系:
- 若 \(\theta = 0^\circ\),\(\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}|\)
- 若 \(\theta = 180^\circ\),\(\vec{a} \cdot \vec{b} = -|\vec{a}| |\vec{b}|\)
- 若 \(\theta < 90^\circ\),\(\vec{a} \cdot \vec{b} > 0\)
- 若 \(\theta = 90^\circ\),\(\vec{a} \cdot \vec{b} = 0\)
- 若 \(\theta > 90^\circ\),\(\vec{a} \cdot \vec{b} < 0\)
double Dot(Point a, Point b) { //点积
return a.x * b.x + a.y * b.y;
}
叉积
对于 \(\vec{a} = (x_1, y_1)\),\(\vec{b} = (x_2, y_2)\),\(\vec{a} \times \vec{b} = x_1 y_2 - x_2 y_1\)
向量位置与叉积大小的关系:
- 若 \(\vec{a} \parallel \vec{b}\),\(\vec{a} \times \vec{b} = 0\)
- 若 \(\vec{a}\) 在 \(\vec{b}\) 的右侧,\(\vec{a} \times \vec{b} > 0\)
- 若 \(\vec{a}\) 在 \(\vec{b}\) 的左侧,\(\vec{a} \times \vec{b} < 0\)
double Cro(Point a, Point b) { //叉积
return a.x * b.y - a.y * b.x;
}
点,向量的旋转
对于点 \(P(x, y)\) 或向量 \(\vec{a} = (x, y)\),将其顺时针旋转 \(\theta\) 角度(点:关于原点,向量:关于起点):
Point turn_P(Point a, double theta) {//点A或向量A顺时针旋转theta(弧度)
double x = a.x * cos(theta) + a.y * sin(theta);
double y = -a.x * sin(theta) + a.y * cos(theta);
return Point(x, y);
}
将点 \(A(x, y)\) 绕点 \(B(x_0, y_0)\) 顺时针旋转 \(\theta\) 角度:
Point turn_PP(Point a, Point b, double theta) {//将点A绕点B顺时针旋转theta(弧度)
double x = (a.x - b.x) * cos(theta) + (a.y - b.y) * sin(theta) + b.x;
double y = -(a.x - b.x) * sin(theta) + (a.y - b.y) * cos(theta) + b.y;
return Point(x, y);
}
点与线段
判断点\(P\)是否在线段\(AB\)上
int pan_PL(Point p, Point a, Point b){ //判断点P是否在线段AB上
return !dcmp(Cro(p - a, b - a)) && dcmp(Dot(p - a, p - b)) <= 0;
}
点\(P\)到线段\(AB\)的距离
bool operator== (Point a, Point b) { //两点坐标重合则相等
return !dcmp(a.x - b.x) && !dcmp(a.y - b.y);
}
double dis_PL(Point p, Point a, Point b){ //点P到线段AB距离
if (a == b) return Len(p - a);//AB重合
Point x = p - a, y = p - b, z = b - a;
if (dcmp(Dot(x, z)) < 0) return Len(x);//P距离A更近
if (dcmp(Dot(y, z)) > 0) return Len(y);//P距离B更近
return Abs(Cro(x,z) / Len(z));//面积除以底边长
}
点与直线
判断点\(P\)是否在直线\(AB\)上
int pan_PL_(Point p, Point a, Point b) { //判断点P是否在直线AB上
return !dcmp(Cro(p - a, b - a)); //PA,AB共线
}
点\(P\)到直线\(AB\)的垂足\(F\)
Point FootPoint(Point p, Point a, Point b) { //点P到直线AB的垂足
Point x = p - a, y = p - b, z = b - a;
double len1 = Dot(x, z) / Len(z), len2 = -1.0 * Dot(y, z) / Len(z); //分别计算AP,BP在AB,BA上的投影
return a + z * (len1 / (len1 + len2));//点A加上向量AF
}
点\(P\)关于直线\(AB\)的对称点
Point Symmetry_PL(Point p, Point a, Point b) { //点P关于直线AB的对称点
return p + (FootPoint(p, a, b) - p) * 2;//将PF延长一倍即可
}
点\(P\)在直线\(AB\)上的投影
double get_line_projection(Point p, Point a, Point b) {
Point v = b - a;
return a + v * (Dot(v, p - a) / Dot(v, v));
}
线与线
两直线\(AB\),\(CD\)的交点\(Q\)
Point cross_LL(Point a, Point b, Point c, Point d) { //两直线AB,CD的交点
Point x = b - a, y = d - c, z = a - c;
return a + x * (Cro(y, z) / Cro(x, y));//点A加上向量AF
}
判断直线\(AB\)与线段\(CD\)是否相交
int pan_cross_L_L(Point a, Point b, Point c, Point d) { //判断直线AB与线段CD是否相交
return pan_PL(cross_LL(a, b, c, d), c, d); //直线AB与直线CD的交点在线段CD上
}
判断两线段\(AB\),\(CD\)是否相交
int pan_cross_LL(Point a, Point b, Point c, Point d) { //判断两线段AB, CD是否相交
double c1 = Cro(b - a, c - a), c2 = Cro(b - a, d - a);
double d1 = Cro(d - c, a - c), d2 = Cro(d - c, b - c);
return dcmp(c1) * dcmp(c2) < 0 && dcmp(d1) * dcmp(d2) < 0;//分别在两侧
}
点与多边形
判断点 \(A\) 是否在任意多边形 \(Poly\) 以内(射线法)
int PIP(Point *P, int n, Point a) { //[射线法]判断点A是否在任意多边形Poly以内
int cnt = 0;
double tmp;
for (int i = 1; i <= n; ++ i) {
int j = i < n ? i + 1 : 1;
if (pan_PL(a, P[i], P[j])) return 2; //点在多边形上
if (a.y >= min(P[i].y, P[j].y) && a.y < max(P[i].y, P[j].y)) //纵坐标在该线段两端点之间
tmp = P[i].x + (a.y - P[i].y) / (P[j].y - P[i].y) * (P[j].x - P[i].x), cnt += dcmp(tmp - a.x) > 0; //交点在A右方
}
return cnt & 1;//穿过奇数次则在多边形以内
}
判断点 \(A\) 是否在凸多边形 \(Poly\) 以内(二分法)
int judge(Point a, Point L, Point R) { //判断AL是否在AR右边
return dcmp(Cro(L - a, R - a)) > 0;//必须严格以内
}
int PIP_(Point *P, int n, Point a) { //[二分法]判断点A是否在凸多边形Poly以内
//点按逆时针给出
if (judge(P[1], a, P[2]) || judge(P[1], P[n], a)) return 0; //在P[1_2]或P[1_n]外
if (pan_PL(a, P[1], P[2]) || pan_PL(a, P[1], P[n])) return 2; //在P[1_2]或P[1_n]上
int l = 2, r = n - 1;
while (l < r) {//二分找到一个位置pos使得P[1]_A在P[1_pos], P[1_(pos+1)]之间
int mid = l + r + 1>>1;
if (judge(P[1], P[mid], a)) l = mid;
else r = mid - 1;
}
if (judge(P[l], a, P[l + 1])) return 0;//在P[pos_(pos + 1)]外
if (pan_PL(a, P[l], P[l + 1])) return 2;//在P[pos_(pos + 1)]上
return 1;
}
线与多边形
-
判断线段 \(AB\) 是否在任意多边形 \(Poly\) 以内。不相交且两端点 \(A, B\) 均在多边形以内。
-
判断线段 \(AB\) 是否在凸多边形 \(Poly\) 以内。两端点 \(A, B\) 均在多边形以内。
多边形与多边形
判断任意两个多边形是否相离:属于不同多边形的任意两边都不相交且一个多边形上的任意点都不被另一个多边形所包含。
int judge_PP(Point *A, int n, Point *B, int m) { //[判断多边形A与多边形B是否相离]
for (int i1 = 1; i1 <= n; ++ i1) {
int j1 = i1 < n ? i1 + 1 : 1;
for (int i2 = 1; i2 <= m; ++ i2) {
int j2 = i2 < m ? i2 + 1 : 1;
if (pan_cross_LL(A[i1], A[j1], B[i2], B[j2])) return 0;//两线段相交
if (PIP(B, m, A[i1]) || PIP(A, n, B[i2])) return 0;//点包含在内
}
}
return 1;
}
任意多边形面积
double PolyArea(Point *P, int n) { //[任意多边形P的面积]
double S = 0;
for (int i = 1; i <= n; ++ i) S += Cro(P[i], P[i < n ? i + 1 : 1]);
return S / 2.0;
}
匹克定理
每个点都必须在整数点上
任意三点组成的面积
//A, B:直线上一点,C:待判断关系的点
int relation(Point A, Point B, Point C) {
// 1 left -1 right 0 in
int c = sign(Cro((B - A), (C - A)));
if (c < 0) return 1;
else if (c > 0) return -1;
return 0;
}
三角形面积
\(S = \frac{1}{2} * |\vec{ab} * \vec{ac}|\)
#include <bits/stdc++.h>
using namespace std;
int x[3], y[3];
double get(double x1, double y1, double x2, double y2) {
return x1 * y2 - y1 * x2;
}
int main() {
double s = 0;
for (int i = 0; i < 3; ++ i) {
cin >> x[i] >> y[i];
}
s = fabs(get(x[1] - x[0], y[1] - y[0], x[2] - x[0], y[2] - y[0]));
printf("%.2lf", s / 2);
return 0;
}
三点是否共线
bool check(Point A, Point B, Point C) {
return (B.x - A.x) * (C.y - B.y) - (B.y - A.y) * (C.x - B.x) == 0;
}
三点确定圆
设 \(x^2 + y^2 + Dx + Ey + F = 0\),圆心为 \(O\),半径为 \(r\),带入三点 \(A(x_1, y_1)\),\(B(x_2, y_2)\),\(C(x_3, y_3)\),解得:
#define S(a) ((a) * (a))
struct Circle {
Point O;
double r;
Circle(Point P, double R = 0) {
O = P, r = R;
}
};
Circle getCircle(Point A, Point B, Point C) { //[三点确定一圆]暴力解方程
double x1 = A.x, y1 = A.y, x2 = B.x, y2 = B.y, x3 = C.x, y3 = C.y;
double D = ((S(x2) + S(y2) - S(x3) - S(y3)) * (y1 - y2) - (S(x1) + S(y1) - S(x2) - S(y2)) * (y2 - y3)) / ((x1 - x2) * (y2 - y3) - (x2 - x3) * (y1 - y2));
double E = (S(x1) + S(y1) - S(x2) - S(y2) + D * (x1 - x2)) / (y2 - y1);
double F =- (S(x1) + S(y1) + D * x1 + E * y1);
return Circle(Point(-D / 2.0, -E / 2.0), sqrt((S(D) + S(E) - 4.0 * F) / 4.0));
}
向量求三角形垂心
inline Circle getcircle(Point A, Point B, Point C) { //【三点确定一圆】向量垂心法
Point P1 = (A + B) * 0.5, P2 = (A + C) * 0.5;
Point O = cross_LL(P1, P1 + Normal(B - A), P2, P2 + Normal(C - A));
return Circle(O, Len(A - O));
}
多面体欧拉定理
顶点数 - 棱长数 + 表面数 = \(2\)
凸包
农夫约翰想要建造一个围栏来围住奶牛。
构建这个围栏时,必须将若干个奶牛们喜爱的地点都包含在围栏内。
现在给定这些地点的具体坐标,请你求出将这些地点都包含在内的围栏的最短长度是多少。
注意:围栏边上的点也算处于围栏内部。
输入格式
第一行包含整数 \(N\),表示奶牛们喜爱的地点数目。
接下来 \(N\) 行,每行包含两个实数 \(X_i,Y_i\),表示一个地点的具体坐标。
输出格式
输出一个实数,表示围栏最短长度。
保留两位小数。
输入样例
4
4 8
4 12
5 9.3
7 8
输出样例
12.00
说明
把所有点以横坐标为第一关键字,纵坐标为第二关键字排序
排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形,我们如果从一个点出发逆时针走,轨迹总是“左拐”的,一旦出现右拐,就说明这一段不在凸包上。因此我们可以用一个单调栈来维护 上下凸壳
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 10010;
int n;
PDD q[N];
int stk[N];
bool used[N];
//used数组表示这个点是否已经在底边上了,如果在了,就不用考虑把他放在顶边上了。
//注意在我们在求顶的时候,要把used[0]变成false
//因为我们求的闭包长度 【首是0 末是0 闭环】
double get_dist(PDD a, PDD b) {
double dx = a.x - b.x;
double dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
PDD operator-(PDD a, PDD b) {
return {a.x - b.x, a.y - b.y};
}
double cross(PDD a, PDD b) {
return a.x * b.y - a.y * b.x;
}
//判断顺时针还是逆时针 有向面积
double area(PDD a, PDD b, PDD c) {
return cross(b - a, c - a);
}
double andrew() { //Andrew算法
// pair 默认对first升序,当first相同时对second升序;
sort(q, q + n);
int top = 0;
for (int i = 0; i < n; i ++ ) {
while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0) {
// 凸包边界上的点即使被从栈中删掉,也不能删掉used上的标记
if (area(q[stk[top - 1]], q[stk[top]], q[i]) < 0) //不共线直接删掉
used[stk[top -- ]] = false;
else top -- ; //共线删掉,但不要置false因为在底边上
}
stk[ ++ top] = i; //加入当前栈
used[i] = true; //置true
}
used[0] = false; //第一个点置false
for (int i = n - 1; i >= 0; i -- ) {
if (used[i]) continue;
while (top >= 2 && area(q[stk[top - 1]], q[stk[top]], q[i]) <= 0)
top -- ;
stk[ ++ top] = i;
}
double res = 0;
for (int i = 2; i <= top; i ++ )
res += get_dist(q[stk[i - 1]], q[stk[i]]);
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);
double res = andrew();
printf("%.2lf\n", res);
return 0;
}
半平面交
半平面交是指多个半平面的交集。因为半平面是点集,所以点集的交集仍然是点集。在平面直角坐标系 围成一个区域。
逆时针给出 \(n\) 个凸多边形的顶点坐标,求它们交的面积。
例如 \(n=2\) 时,两个凸多边形如下图:
则相交部分的面积为 \(5.233\)。
输入格式
第一行有一个整数 \(n\),表示凸多边形的个数,以下依次描述各个多边形。
第 \(i\) 个多边形的第一行包含一个整数 \(m_i\),表示多边形的边数;以下 \(m_i\) 行每行两个整数,逆时针给出各个顶点的坐标。
输出格式
仅包含一个实数,表示相交部分的面积,保留三位小数。
输入样例
2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0
输出样例
5.233
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double,double> PDD;
const int N = 510;
const double eps = 1e-8;
int cnt;
struct Line {
PDD st, ed; //记录当前直线的起点坐标和终点坐标
}line[N]; //存储所有直线
PDD pg[N], ans[N]; //存储凸多边形的所有点的临时数组,存储半平面交上的所有点
int q[N]; //双端队列
int sign(double x) { //判断 x 的正负性
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int dcmp(double x, double y) { //比较 x 和 y 的大小
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
double get_angle(const Line& a) { //求向量 a 的角度
return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);
}
PDD operator-(PDD a, PDD b) { //重载减号运算法
return {a.x - b.x, a.y - b.y};
}
double cross(PDD a, PDD b) { //计算 a 和 b 的叉积
return a.x * b.y - a.y * b.x;
}
double area(PDD a, PDD b, PDD c) { //计算 ab 和 ac 构成的平行四边形的有向面积
return cross(b - a, c - a);
}
bool cmp(const Line& a, const Line& b) { //比较函数:按照直线的角度从小到大排序
double A = get_angle(a), B = get_angle(b);
if (!dcmp(A, B)) return area(a.st, a.ed, b.ed) < 0; //如果两条直线角度相同,则将靠左的排在前面
return A < B;
}
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) { //求两个点向式直线的交点
auto u = p - q;
double t = cross(w, u) / cross(v, w);
return {p.x + v.x * t, p.y + v.y * t};
}
PDD get_line_intersection(Line a, Line b) { //求直线 a 和直线 b 的交点
return get_line_intersection(a.st, a.ed - a.st, b.st, b.ed - b.st);
}
// bc的交点是否在a的右侧
bool on_right(Line& a, Line& b, Line& c) { //判断 b 和 c 的交点是否在 a 的右侧
auto o = get_line_intersection(b, c); //求 b 和 c 的交点
return sign(area(a.st, a.ed, o)) <= 0;
}
double half_plane_intersection() { //求半平面交
sort(line, line + cnt, cmp); //将所有直线按照角度从小到大排序
int hh = 0, tt = -1;
for (int i = 0; i < cnt; i ++ ) {
if (i && !dcmp(get_angle(line[i]), get_angle(line[i - 1]))) continue; //角度相同的直线只考虑最靠左的一条
while (hh + 1 <= tt && on_right(line[i], line[q[tt - 1]], line[q[tt]])) tt -- ; //删除队尾无用直线
while (hh + 1 <= tt && on_right(line[i], line[q[hh]], line[q[hh + 1]])) hh ++ ; //删除队头无用直线
q[ ++ tt] = i; //将当前直线加入队列
}
while (hh + 1 <= tt && on_right(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt -- ; //用队头更换队尾
while (hh + 1 <= tt && on_right(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh ++ ; //用队尾更新队头
q[ ++ tt] = q[hh]; //将队头重复加入队尾
int k = 0;
//求出半平面交上的所有顶点
for (int i = hh; i < tt; i ++ )
ans[k ++ ] = get_line_intersection(line[q[i]], line[q[i + 1]]);
double res = 0; //记录半平面交的面积
for (int i = 1; i + 1 < k; i ++ )
res += area(ans[0], ans[i], ans[i + 1]); //求半平面交(凸多边形)的面积
return res / 2;
}
int main() {
int n, m;
scanf("%d", &n);
while (n -- ) {
scanf("%d", &m);
for (int i = 0; i < m; i ++ ) scanf("%lf%lf", &pg[i].x, &pg[i].y);
for (int i = 0; i < m; i ++ )
line[cnt ++ ] = {pg[i], pg[(i + 1) % m]};
}
double res = half_plane_intersection(); //求半平面交
printf("%.3lf\n", res);
return 0;
}
最小圆覆盖
在一个二维平面上给定 \(N\) 个点,请你画出一个最小的能够包含所有点的圆。
圆的边上的点视作在圆的内部。
输入格式
第一行包含一个整数 \(N\)。
接下来 \(N\) 行,每行包含两个实数,表示一个点的坐标 \((Xi,Yi)\)。
输出格式
第一行输出圆的半径。
第二行输出圆心的坐标。
结果保留 \(10\) 位小数。
输入样例
6
8.0 9.0
4.0 7.5
1.0 2.0
5.1 8.7
9.0 2.0
4.5 1.0
输出样例
5.0000000000
5.0000000000 5.0000000000
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 100010;
const double eps = 1e-12;
const double PI = acos(-1);
int n;
PDD q[N]; // 点的坐标
struct Circle {
PDD p;
double r;
};
int sign(double x) {
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int dcmp(double x, double y) {
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
PDD operator- (PDD a, PDD b) {
return {a.x - b.x, a.y - b.y};
}
PDD operator+ (PDD a, PDD b) {
return {a.x + b.x, a.y + b.y};
}
PDD operator* (PDD a, double t) {
return {a.x * t, a.y * t};
}
PDD operator/ (PDD a, double t) {
return {a.x / t, a.y / t};
}
double operator* (PDD a, PDD b) {
return a.x * b.y - a.y * b.x;
}
// 将向量a顺时针旋转 b
PDD rotate(PDD a, double b) {
return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}
double get_dist(PDD a, PDD b) {
double dx = a.x - b.x;
double dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
// 获取直线 p+vt 和 q+wt 的交点坐标
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) {
auto u = p - q;
double t = w * u / (v * w);
return p + v * t;
}
// 获取线段ab的中垂线: 返回 (起点, 方向)
pair<PDD, PDD> get_line(PDD a, PDD b) {
return {(a + b) / 2, rotate(b - a, PI / 2)};
}
// 给定三个点,返回圆的圆心和半径
Circle get_circle(PDD a, PDD b, PDD c) {
auto u = get_line(a, b), v = get_line(a, c);
auto p = get_line_intersection(u.x, u.y, v.x, v.y);
return {p, get_dist(p, a)};
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);
random_shuffle(q, q + n);
Circle c({q[0], 0});
for (int i = 1; i < n; i ++ )
if (dcmp(c.r, get_dist(c.p, q[i])) < 0) { // 说明q[i]在当前圆外
c = {q[i], 0};
for (int j = 0; j < i; j ++ )
if (dcmp(c.r, get_dist(c.p, q[j])) < 0) { // 说明q[j]在当前圆外
// 以q[i]、q[j]为直径的圆
c = {(q[i] + q[j]) / 2, get_dist(q[i], q[j]) / 2};
for (int k = 0; k < j; k ++ )
if (dcmp(c.r, get_dist(c.p, q[k])) < 0) // 说明q[j]在当前圆外
c = get_circle(q[i], q[j], q[k]);
}
}
printf("%.10lf\n", c.r);
printf("%.10lf %.10lf\n", c.p.x, c.p.y);
return 0;
}
三维计算几何基础与三维凸包
发强公司生产了一种金属制品,是由一些笔直的金属条连接起来的,金属条和别的金属条在交点上被焊接在了一起。
现在由于美观需要,在这个产品用一层特殊的材料包裹起来。
公司为了节约成本,希望消耗的材料最少(不计裁剪时的边角料的损失)。
编程,输入包括该产品的顶点的个数,以及所有顶点的坐标;请计算出包裹这个产品所需要的材料的最小面积。
结果要求精确到小数点后第六位(四舍五入)。
输入格式
输入文件由若干行组成:
第 \(1\) 行是一个整数 \(n\),表示顶点的个数;第 \(2\) 行到第 \(n+1\) 行,每行是 \(3\) 个实数 \(x_i,y_i,z_i\),表示第 \(i\) 个顶点的坐标。
每个顶点的位置各不相同。
输出格式
输出文件只有一个实数,表示包裹一个该产品所需的材料面积的最小值。
输入样例
4
0 0 0
1 0 0
0 1 0
0 0 1
输出样例
2.366025
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 210;
const double eps = 1e-12;
int n, m; //点数、面数
bool g[N][N]; //g[i][j] 表示 (i, j) 对应的面有没有被照到
double rand_eps() { //返回一个极小的随机值
return ((double)rand() / RAND_MAX - 0.5) * eps;
}
struct Point {
double x, y, z;
void shake() { //将当前点进行随机扰动
x += rand_eps(), y += rand_eps(), z += rand_eps();
}
Point operator- (Point t) { //重载向量减法
return {x - t.x, y - t.y, z - t.z};
}
double operator& (Point t) { //重载点积
return x * t.x + y * t.y + z * t.z;
}
Point operator* (Point t) { //重载叉积
return {y * t.z - t.y * z, z * t.x - x * t.z, x * t.y - y * t.x};
}
double len() { //求模长
return sqrt(x * x + y * y + z * z);
}
}q[N]; //存储所有点
struct Plane {
int v[3]; //三角形平面的三个顶点
Point norm() { //求平面法向量
return (q[v[1]] - q[v[0]]) * (q[v[2]] - q[v[0]]);
}
double area() { //求平面的面积
return norm().len() / 2;
}
bool above(Point a) { //判断 t 是否在平面的上方
return ((a - q[v[0]]) & norm()) >= 0;
}
}plane[N], np[N]; //存储所有三角形平面,np 是备份数组
void get_convex_3d() {//最开始由头三个点构成凸包,有正、反两面
plane[m ++ ] = {0, 1, 2};
plane[m ++ ] = {2, 1, 0};
for (int i = 3; i < n; i ++ ) {
int cnt = 0; //记录加入新点后所有的面
for (int j = 0; j < m; j ++ ) {
bool t = plane[j].above(q[i]); //记录当前点是否在当前平面的上方
if (!t) np[cnt ++ ] = plane[j]; //如果当前点在当前平面下方,则当前平面应该保留
for (int k = 0; k < 3; k ++ )
g[plane[j].v[k]][plane[j].v[(k + 1) % 3]] = t; //记录当前面的每条边是否被照到
}
//在分界线上构造新面
for (int j = 0; j < m; j ++ )
for (int k = 0; k < 3; k ++ ) {
int a = plane[j].v[k], b = plane[j].v[(k + 1) % 3];
if (g[a][b] && !g[b][a]) //如果当前边是分界线,构建新面
np[cnt ++ ] = {a, b, i};
}
m = cnt;
for (int j = 0; j < m; j ++ ) plane[j] = np[j]; //将新凸包拷贝回原数组
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) {
scanf("%lf%lf%lf", &q[i].x, &q[i].y, &q[i].z);
q[i].shake(); //将当前点进行随机扰动
}
get_convex_3d(); //求三维凸包
double res = 0; //记录三维凸包的面积
for (int i = 0; i < m; i ++ )
res += plane[i].area();
printf("%lf\n", res);
return 0;
}
旋转卡壳
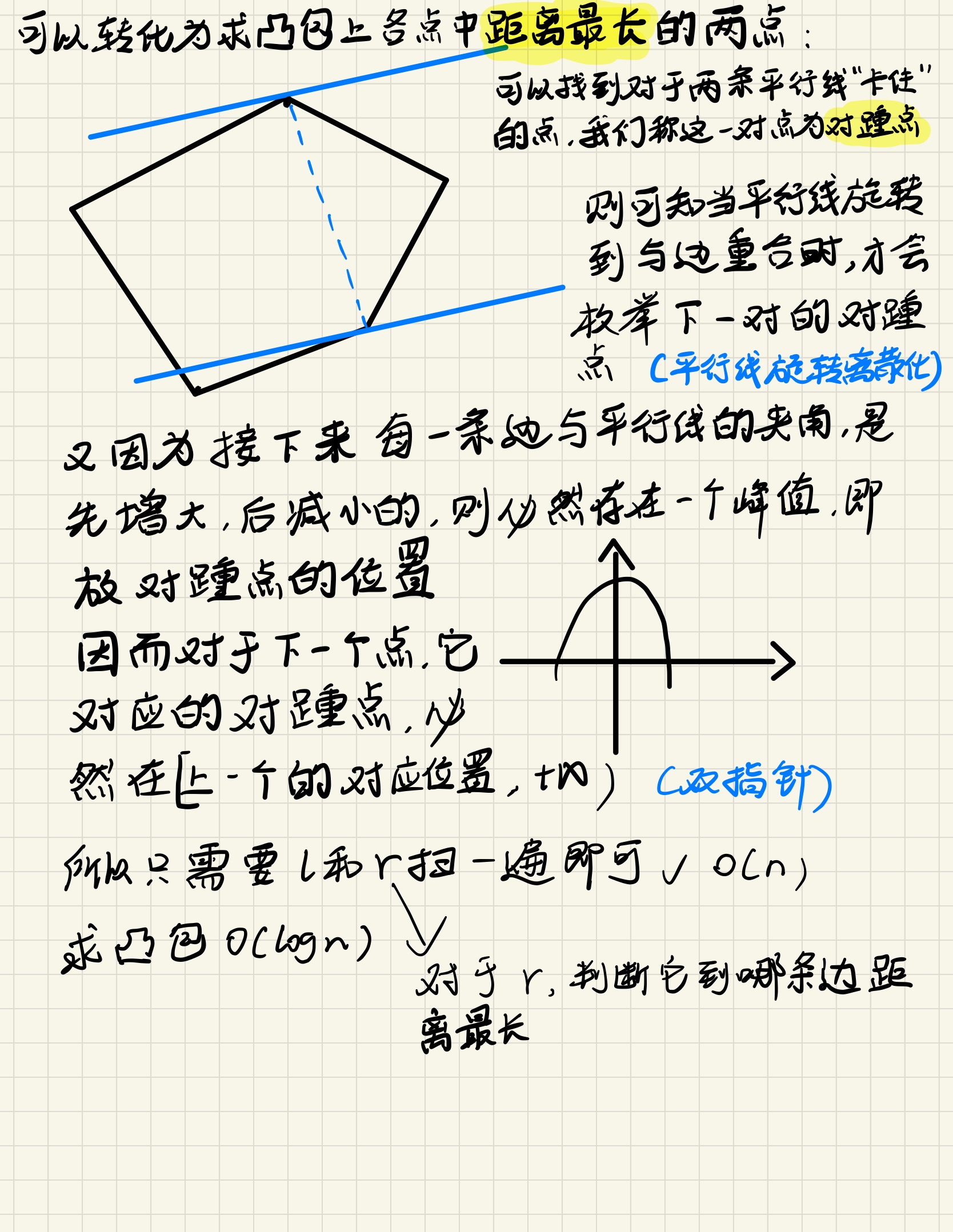
给定一个二维平面,平面上有 \(N\) 个点。每个点的位置可以用一对整数坐标 \((x, y)\) 表示,求出平面上距离最远的点对之间的距离。
输入格式
第一行包含一个整数 \(N\)。
接下来 \(N\) 行,每行包含两个整数 \(x,y\),表示一个点的位置坐标。
输出格式
输出一个整数,表示距离最远的点对之间的距离的平方。
输入样例
4
0 0
0 1
1 1
1 0
输出样例
2
说明
第一个点和第三个点之间的距离最远,为 \(\sqrt2\)。
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 50010;
int n;
PII q[N]; //存储所有点的坐标
int stk[N], top; //栈,存储凸包
bool used[N]; //记录每个点是否在凸包中
PII operator- (PII a, PII b) { //重载向量减法
return {a.x - b.x, a.y - b.y};
}
int operator* (PII a, PII b) { //重载叉乘
return a.x * b.y - a.y * b.x;
}
int area(PII a, PII b, PII c) { //求 ab 和 ac 构成的平行四边形的有向面积
return (b - a) * (c - a);
}
int get_dist(PII a, PII b) { //求 a 和 b 的距离的平方
int dx = a.x - b.x;
int dy = a.y - b.y;
return dx * dx + dy * dy;
}
void get_convex() { //求二维凸包
sort(q, q + n); //将所有点按照横、纵坐标从小到大排序
//求下凸包
for (int i = 0; i < n; i ++ ) {
//不保留直线上的点
while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0) {
if (area(q[stk[top - 2]], q[stk[top - 1]], q[i]) < 0)
used[stk[ -- top]] = false;
else top -- ; //如果点在直线上则不重置标记
}
stk[top ++ ] = i;
used[i] = true;
}
//求上凸包
used[0] = false; //将起点的标记重置
for (int i = n - 1; i >= 0; i -- ) {
if (used[i]) continue; //如果当前点已经在凸包中,直接跳过
while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) <= 0)
top -- ;
stk[top ++ ] = i;
}
top -- ; //起点加入了两次,删掉一次
}
int rotating_calipers() { //旋转卡壳求最远点对的距离,并返回距离的平方
if (top <= 2) return get_dist(q[0], q[n - 1]); //如果多点共线,则他们之间的距离就是答案
int res = 0; //记录最远距离
for (int i = 0, j = 2; i < top; i ++ ) {
auto d = q[stk[i]], e = q[stk[i + 1]];
while (area(d, e, q[stk[j]]) < area(d, e, q[stk[j + 1]])) j = (j + 1) % top; //找出距离当前边最远的点
res = max(res, max(get_dist(d, q[stk[j]]), get_dist(e, q[stk[j]]))); //更新答案
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &q[i].x, &q[i].y);
get_convex(); //求二维凸包
printf("%d\n", rotating_calipers()); //旋转卡壳求最远点对的距离
return 0;
}
最小矩形覆盖
已知平面上不共线的一组点的坐标,求覆盖这组点的面积最小的矩形。
输出矩形的面积和四个顶点的坐标。
输入格式
第一行包含一个整数 \(n\),表示点的数量。
接下来 \(n\) 行,每行包含两个用空格隔开的浮点数,表示一个点的 \(x\) 坐标和 \(y\) 坐标。不用科学计数法,但如果小数部分为 0,则可以写成整数。
输出格式
共 5 行,第一行输出一个浮点数,表示所求得的覆盖输入点集的最小矩形的面积。
接下来的 4 行,每行包含两个用空格隔开的浮点数,表示所求矩形的一个顶点的 \(x\) 坐标和 \(y\) 坐标。
先输出 \(y\) 坐标最小的顶点的 \(x, y\) 坐标,如果有两个点的 \(y\) 坐标同时达到最小,则先输出 \(x\) 坐标较小者的 \(x, y\) 坐标。
然后,按照逆时针的顺序输出其他三个顶点的坐标。
不用科学计数法,精确到小数点后 5 位,后面的 0 不可省略。
答案不唯一,输出任意一组正确结果即可。
输入样例
6
1.0 3.00000
1 4.00000
2.00000 1
3 0.00000
3.00000 6
6.0 3.0
输出样例
18.00000
3.00000 0.00000
6.00000 3.00000
3.00000 6.00000
0.00000 3.00000
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 50010;
const double eps = 1e-12, INF = 1e20;
const double PI = acos(-1);
int n;
PDD q[N]; //存储每个点的坐标
PDD ans[N]; //逆时针存储最小覆盖矩形的四个顶点
double min_area = INF; //记录最小覆盖矩形的面积
int stk[N], top; //栈,存储凸包
bool used[N]; //记录每个点是否在凸包上
int sign(double x) { //符号函数
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int dcmp(double x, double y) { //比较函数
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
PDD operator+ (PDD a, PDD b) { //重载向量加法
return {a.x + b.x, a.y + b.y};
}
PDD operator- (PDD a, PDD b) { //重载向量减法
return {a.x - b.x, a.y - b.y};
}
PDD operator* (PDD a, double t) { //重载数乘
return {a.x * t, a.y * t};
}
PDD operator/ (PDD a, double t) { //重载数除
return {a.x / t, a.y / t};
}
double operator* (PDD a, PDD b) { //重载叉乘
return a.x * b.y - a.y * b.x;
}
double operator& (PDD a, PDD b) { //重载点乘
return a.x * b.x + a.y * b.y;
}
double area(PDD a, PDD b, PDD c) { //计算 ab 和 ac 构成的平行四边形的有向面积
return (b - a) * (c - a);
}
double get_len(PDD a) { //计算向量 a 的模长
return sqrt(a & a);
}
double project(PDD a, PDD b, PDD c) { //计算 ac 在 ab 上的投影的长度
return ((b - a) & (c - a)) / get_len(b - a);
}
PDD norm(PDD a) { //求 a 的单位向量
return a / get_len(a);
}
PDD rotate(PDD a, double b) { //将 a 顺时针旋转 b 弧度
return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}
void get_convex() {
sort(q, q + n); //将所有点按照横、纵坐标从小到大排序
//求下凸包
for (int i = 0; i < n; i ++ ) {
while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0)
used[stk[ -- top]] = false; //如果点在直线上,则不能重置标记
stk[top ++ ] = i;
used[i] = true;
}
//求上凸包
used[0] = false;
for (int i = n - 1; i >= 0; i -- ) {
if (used[i]) continue; //如果当前点已经在凸包上,直接跳过
while (top >= 2 && sign(area(q[stk[top - 2]], q[stk[top - 1]], q[i])) >= 0)
top -- ;
stk[top ++ ] = i;
}
reverse(stk, stk + top);
top -- ; //起点加入了两次,删掉一次
}
void rotating_calipers() { //旋转卡壳
for (int i = 0, a = 2, b = 1, c = 2; i < top; i ++ ) { //a 表示上边界的点,b 表示右边界的点,c 表示左边界的点
auto d = q[stk[i]], e = q[stk[i + 1]];
while (dcmp(area(d, e, q[stk[a]]), area(d, e, q[stk[a + 1]])) < 0) a = (a + 1) % top; //更新 a
while (dcmp(project(d, e, q[stk[b]]), project(d, e, q[stk[b + 1]])) < 0) b = (b + 1) % top; //更新 b
if (!i) c = a; //最开始 c 要从 a 开始往右走,才能保证走到左边界
while (dcmp(project(d, e, q[stk[c]]), project(d, e, q[stk[c + 1]])) > 0) c = (c + 1) % top;//更新 c
auto x = q[stk[a]], y = q[stk[b]], z = q[stk[c]];
auto h = area(d, e, x) / get_len(e - d); //求矩形的高
auto w = ((y - z) & (e - d)) / get_len(e - d); //求矩形的宽
if (h * w < min_area) { //更新最小覆盖矩形
min_area = h * w; //更新最小覆盖矩形的面积
//更新最小覆盖矩形的四个顶点
ans[0] = d + norm(e - d) * project(d, e, y); //右下角
ans[3] = d + norm(e - d) * project(d, e, z); //左下角
auto u = norm(rotate(e - d, -PI / 2));
ans[1] = ans[0] + u * h; //右上角
ans[2] = ans[3] + u * h; //左上角
}
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);
get_convex(); //求二维凸包
rotating_calipers(); //旋转卡壳
//找出最小的顶点坐标
int k = 0;
for (int i = 1; i < 4; i ++ )
if (dcmp(ans[i].y, ans[k].y) < 0 || !dcmp(ans[i].y, ans[k].y) && dcmp(ans[i].x, ans[k].x) < 0)
k = i;
printf("%.5lf\n", min_area);
for (int i = 0; i < 4; i ++, k ++ ) {
auto x = ans[k % 4].x, y = ans[k % 4].y;
//C++ 中 -0.00...001 四舍五入后会得到 -0.00...000,因此需要特判
if (!sign(x)) x = 0;
if (!sign(y)) y = 0;
printf("%.5lf %.5lf\n", x, y);
}
return 0;
}
三角剖分
Updog 正在用望远镜观察一个飞行物。
望远镜的视野可以描述为一个圆,其圆心位于原点,半径为 \(R\)。
飞行物可视作一个 \(N\) 个顶点的简单多边形。
Updog 希望知道飞行物处于望远镜视野之内的部分的面积。
输入格式
本题包含多组测试数据。
对于每组数据,第一行包含一个实数 \(R\)。
第二行包含一个整数 \(N\)。
接下来 \(N\) 行,每行包含两个实数 \(x_i,y_i\),表示一个顶点的坐标。相邻两行描述的顶点在多边形中也是相邻的。
输出格式
每组数据输出一行一个实数,表示答案。
结果四舍五入保留两位小数。
输入样例
10
3
0 20
10 0
-10 0
输出样例
144.35
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 55;
const double eps = 1e-8;
const double PI = acos(-1);
double R;
int n;
PDD q[N], r; //存储多边形所有顶点, //圆心
int sign(double x) { //符号函数
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int dcmp(double x, double y) { //比较函数
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
PDD operator+ (PDD a, PDD b) { //重载向量加法
return {a.x + b.x, a.y + b.y};
}
PDD operator- (PDD a, PDD b) { //重载向量减法
return {a.x - b.x, a.y - b.y};
}
PDD operator* (PDD a, double t) { //重载数乘
return {a.x * t, a.y * t};
}
PDD operator/ (PDD a, double t) { //重载数除
return {a.x / t, a.y / t};
}
double operator* (PDD a, PDD b) { //重载叉乘
return a.x * b.y - a.y * b.x;
}
double operator& (PDD a, PDD b) { //重载点乘
return a.x * b.x + a.y * b.y;
}
double area(PDD a, PDD b, PDD c) { //求 ab 和 ac 构成的平行四边形的有向面积
return (b - a) * (c - a);
}
double get_len(PDD a) { //求向量 a 的长度
return sqrt(a & a);
}
double get_dist(PDD a, PDD b) { //求 a 和 b 的距离
return get_len(b - a);
}
double project(PDD a, PDD b, PDD c) { //求 ac 在 ab 上的投影的长度
return ((c - a) & (b - a)) / get_len(b - a);
}
PDD rotate(PDD a, double b) { //将 a 顺时针旋转 b 弧度
return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}
PDD norm(PDD a) { //求向量 a 的单位向量
return a / get_len(a);
}
bool on_segment(PDD p, PDD a, PDD b) { //判断 p 是否在 ab 上
return !sign((p - a) * (p - b)) && sign((p - a) & (p - b)) <= 0; //pa, pb 平行并且方向相反,说明 p 在 ab 上
}
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) { //求两个点向式直线的交点
auto u = p - q;
auto t = w * u / (v * w);
return p + v * t;
}
//求圆和直线 ab 的两个交点 pa, pb,并返回 mind
//如果是情况 5,mind 表示 p 到 ab 的垂线的长度,否则 mind 表示 p 到 a 和 b 的最短距离
double get_circle_line_intersection(PDD a, PDD b, PDD& pa, PDD& pb) {
auto e = get_line_intersection(a, b - a, r, rotate(b - a, PI / 2)); //求 p 到 ab 的垂足
auto mind = get_dist(r, e); //计算 p 到 e 的距离
if (!on_segment(e, a, b)) mind = min(get_dist(r, a), get_dist(r, b)); //如果不是情况 5,修改 mind 的定义
if (dcmp(R, mind) <= 0) return mind; //如果是情况 2,则不需要用到 pa, pb,直接返回
auto len = sqrt(R * R - get_dist(r, e) * get_dist(r, e)); //勾股定理求 e 到 ab 和圆的交点的距离
pa = e + norm(a - b) * len; //求出 pa 的坐标
pb = e + norm(b - a) * len; //求出 pb 的坐标
return mind;
}
double get_sector(PDD a, PDD b) { //求 a 和 b 构成的半径为 R 的有向扇形面积
auto angle = acos((a & b) / get_len(a) / get_len(b)); //计算 a 和 b 的夹角弧度
if (sign(a * b) < 0) angle = -angle; //如果 a 和 b 构成的有向面积是负的,需要将弧度取反
return R * R * angle / 2;
}
double get_circle_triangle_area(PDD a, PDD b) { //求圆和三角形 pab 的交集的面积
auto da = get_dist(r, a), db = get_dist(r, b); //求 a 和 b 到圆心的距离
if (dcmp(R, da) >= 0 && dcmp(R, db) >= 0) return a * b / 2; //情况 1
if (!sign(a * b)) return 0; //如果 p, a, b 三点共线,面积为 0
PDD pa, pb; //记录 ab 和圆的交点,pa 距离 a 更近,pb 距离 b 更近
auto mind = get_circle_line_intersection(a, b, pa, pb); //求 pa, pb,并求出 p 到 ab 的最短距离 mind
if (dcmp(R, mind) <= 0) return get_sector(a, b); //情况 2
if (dcmp(R, da) >= 0) return a * pb / 2 + get_sector(pb, b); //情况 3
if (dcmp(R, db) >= 0) return get_sector(a, pa) + pa * b / 2; //情况 4
return get_sector(a, pa) + pa * pb / 2 + get_sector(pb, b); //情况 5
}
double work() { //求圆和多边形的交集的面积
double res = 0; //记录交集的面积
for (int i = 0; i < n; i ++ )
res += get_circle_triangle_area(q[i], q[(i + 1) % n]);
return fabs(res); //返回面积的绝对值
}
int main() {
while (scanf("%lf%d", &R, &n) != -1) {
for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);
printf("%.2lf\n", work());
}
return 0;
}
矩形面积并
在二维平面中给定 \(n\) 个两条边分别与 \(x\) 轴和 \(y\) 轴平行的矩形,请你求出它们的面积并。
输入格式
第一行包含整数 \(n\)。
接下来 \(n\) 行,每行包含四个整数 \(x_1, y_1, x_2, y_2\),表示其中一个矩形的左下角坐标 \((x_1, y_1)\) 和右上角坐标 \((x_2, y_2)\)。
注意,坐标轴 \(x\) 轴从左向右延伸,\(y\) 轴从下向上延伸。
输出格式
一个整数,表示矩形的面积并。
输入样例
2
10 10 20 20
15 15 25 25
输出样例
175
说明
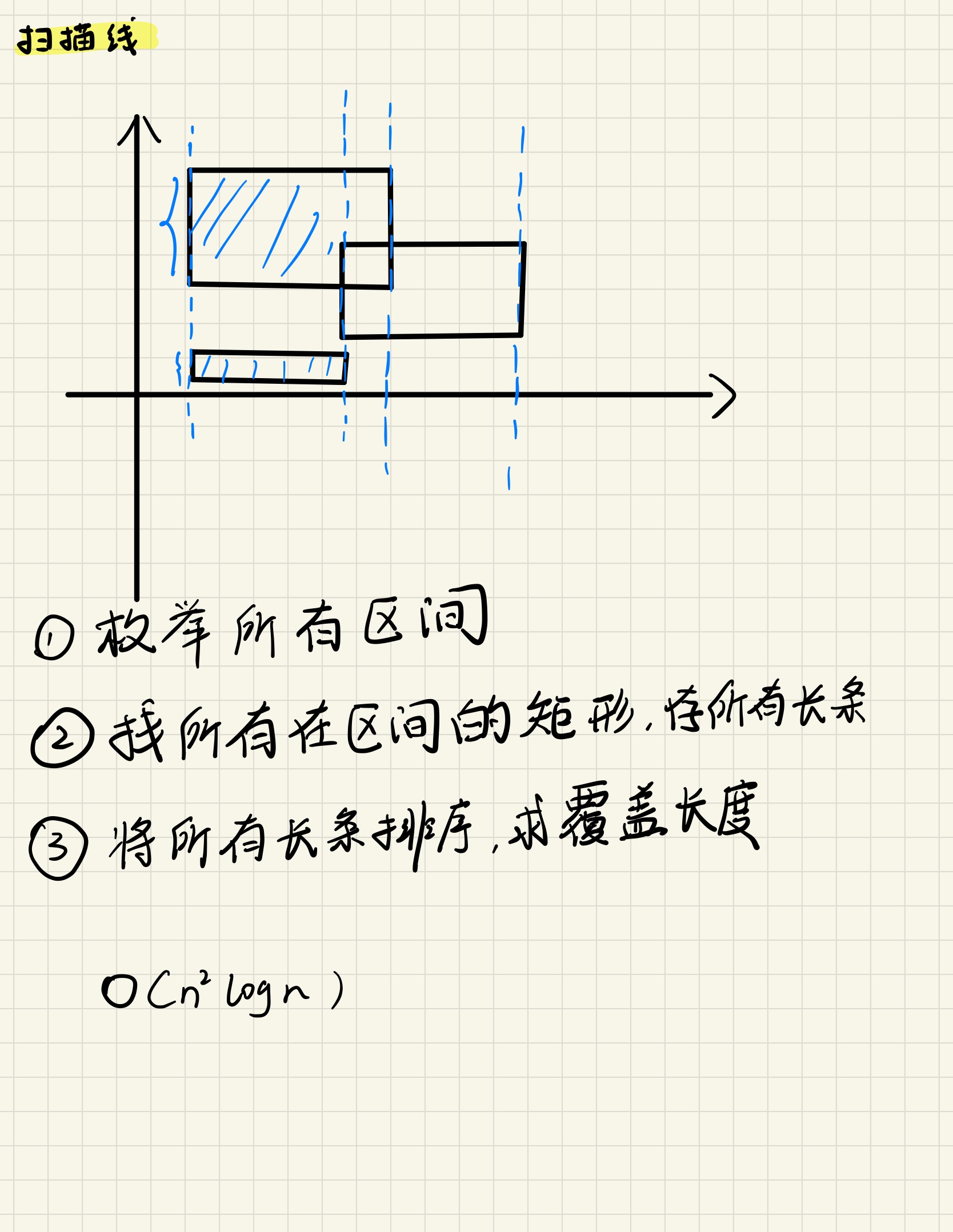
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1010;
int n;
PII l[N], r[N]; // 存储矩形左下角和右上角坐标
PII q[N]; // 存储每个竖直长条中线段
// 计算一个竖直长条的面积
LL range_area(int a, int b) {
// 求需要合并的区间
int cnt = 0;
for (int i = 0; i < n; i ++ )
if (l[i].x <= a && r[i].x >= b)
q[cnt ++ ] = {l[i].y, r[i].y};
if (!cnt) return 0;
// 合并区间、求区间长度并
sort(q, q + cnt);
LL res = 0;
int st = q[0].x, ed = q[0].y;
for (int i = 1; i < cnt; i ++ )
if (q[i].x <= ed) ed = max(ed, q[i].y);
else {
res += ed - st;
st = q[i].x, ed = q[i].y;
}
res += ed - st;
return res * (b - a);
}
int main() {
scanf("%d", &n);
vector<int> xs;
for (int i = 0; i < n; i ++ ) {
scanf("%d%d%d%d", &l[i].x, &l[i].y, &r[i].x, &r[i].y);
xs.push_back(l[i].x), xs.push_back(r[i].x);
}
sort(xs.begin(), xs.end());
LL res = 0;
for (int i = 0; i + 1 < xs.size(); i ++ )
if (xs[i] != xs[i + 1])
res += range_area(xs[i], xs[i + 1]);
printf("%lld\n", res);
return 0;
}
三角形面积并
给出 \(n\) 个三角形,求它们并的面积。
输入格式
第一行为 \(n\),即三角形的个数。
以下 \(n\) 行,每行 6 个实数 \(x_1, y_1, x_2, y_2, x_3, y_3\),代表三角形的顶点坐标。
坐标均为不超过 \(10^6\) 的实数,输入数据保留 1 位小数。
输出格式
输出并的面积 \(u\),保留两位小数。
输入样例
0.0 0.0 2.0 0.0 1.0 1.0
1.0 0.0 3.0 0.0 2.0 1.0
输出样例
1.75
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 110;
const double eps = 1e-8, INF = 1e6;
int n;
PDD tr[N][3]; //存储每个三角形的坐标
PDD q[N]; //记录当前线段上的所有区间
int sign(double x) { //符号函数
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
int dcmp(double x, double y) { //比较函数
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
PDD operator+ (PDD a, PDD b) { //重载向量加法
return {a.x + b.x, a.y + b.y};
}
PDD operator- (PDD a, PDD b) { //重载向量减法
return {a.x - b.x, a.y - b.y};
}
PDD operator* (PDD a, double t) { //重载数乘
return {a.x * t, a.y * t};
}
double operator* (PDD a, PDD b) { //重载叉积
return a.x * b.y - a.y * b.x;
}
double operator& (PDD a, PDD b) { //重载点积
return a.x * b.x + a.y * b.y;
}
bool on_segment(PDD p, PDD a, PDD b) { //判断 p 是否在线段 ab 上
return sign((p - a) & (p - b)) <= 0;
}
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) { //求两个点向式直线的交点
if (!sign(v * w)) return {INF, INF}; //如果两条直线平行,则不存在交点
auto u = p - q;
auto t = w * u / (v * w);
auto o = p + v * t;
//如果交点不在两条直线上,也说明不存在交点
if (!on_segment(o, p, p + v) || !on_segment(o, q, q + w))
return {INF, INF};
return o;
}
double line_area(double a, int side) { //求边界 a 右边的三角形和边界 a 的交集长度
int cnt = 0; //记录线段上区间个数
for (int i = 0; i < n; i ++ ) {
auto t = tr[i];
if (dcmp(t[0].x, a) > 0 || dcmp(t[2].x, a) < 0) continue;
if (!dcmp(t[0].x, a) && !dcmp(t[1].x, a)) { //如果 a 右边的三角形和边界 a 重合,单独处理
if (side) q[cnt ++ ] = {t[0].y, t[1].y}; //这种情况只有边界 a 和右边三角形的交集才需要算
}
else if (!dcmp(t[2].x, a) && !dcmp(t[1].x, a)) { //如果 a 左边的三角形和边界 a 重合,单独处理
if (!side) q[cnt ++ ] = {t[2].y, t[1].y}; //这种情况只有边界 a 和左边三角形的交集才需要算
}
else { //否则说明是一般情况,统一处理
double d[3];
int u = 0;
for (int j = 0; j < 3; j ++ ) {
auto o = get_line_intersection(t[j], t[(j + 1) % 3] - t[j], {a, -INF}, {0, INF * 2});
if (dcmp(o.x, INF)) //如果存在交点
d[u ++ ] = o.y;
}
if (u) { //如果存在交点,则至少两个,最多三个,此时所有交点的纵坐标最小值到纵坐标最大值就是区间
sort(d, d + u);
q[cnt ++ ] = {d[0], d[u - 1]};
}
}
}
if (!cnt) return 0; //如果线段上不存在区间,直接返回 0
for (int i = 0; i < cnt; i ++ )
if (q[i].x > q[i].y)
swap(q[i].x, q[i].y); //保证区间左端点更小
sort(q, q + cnt); //将所有区间从小到大排序
double res = 0, st = q[0].x, ed = q[0].y;
for (int i = 1; i < cnt; i ++ )
if (q[i].x <= ed) ed = max(ed, q[i].y); //区间合并
else {
res += ed - st; //累加每个合并后区间的长度
st = q[i].x, ed = q[i].y;
}
res += ed - st; //累加最后一个合并后区间的长度
return res;
}
double range_area(double a, double b) { //求区间 [a, b] 中的面积
return (line_area(a, 1) + line_area(b, 0)) * (b - a) / 2;
}
int main() {
scanf("%d", &n);
vector<double> xs;
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < 3; j ++ ) {
scanf("%lf%lf", &tr[i][j].x, &tr[i][j].y);
xs.push_back(tr[i][j].x);
}
sort(tr[i], tr[i] + 3); //将每个三角形的三个顶点按照横坐标排序,方便判断三角形和某个区间是否有交集
}
//求所有三角形之间的交点
for (int i = 0; i < n; i ++ ) //枚举第一个三角形
for (int j = i + 1; j < n; j ++ ) //枚举第二个三角形
for (int x = 0; x < 3; x ++ ) //枚举第一个三角形的边
for (int y = 0; y < 3; y ++ ) { //枚举第二个三角形的边
auto o = get_line_intersection(tr[i][x], tr[i][(x + 1) % 3] - tr[i][x],
tr[j][y], tr[j][(y + 1) % 3] - tr[j][y]);
if (dcmp(o.x, INF))
xs.push_back(o.x); //如果当前两条边存在交点,将交点的横坐标存下来
}
//将所有横坐标排序
sort(xs.begin(), xs.end());
double res = 0; //记录答案
for (int i = 0; i + 1 < xs.size(); i ++ )
if (dcmp(xs[i], xs[i + 1])) //如果当前区间宽度不为 0,计算当前区间内的面积
res += range_area(xs[i], xs[i + 1]); //累加当前区间的面积
printf("%.2lf\n", res);
return 0;
}
自适应辛普森积分
给定两个整数 \(a, b\),请计算如下积分
输入格式
共一行,包含两个实数 \(a, b\)。
输出格式
输出一个实数,表示结果。
结果保留 6 位小数。
输入样例
1.0 2.0
输出样例
0.659330
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const double eps = 1e-12;
double f(double x) { //求函数 f(x)
return sin(x) / x;
}
double simpson(double l, double r) { //求 [l, r] 区间内函数的近似面积
auto mid = (l + r) / 2;
return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}
double asr(double l, double r, double s) { //自适应辛普森积分,s 表示 [l, r] 区间内函数的近似面积
auto mid = (l + r) / 2;
auto left = simpson(l, mid), right = simpson(mid, r); //计算左、右区间的近似面积
if (fabs(left + right - s) < eps) return left + right; //如果误差足够小,直接返回近似面积
return asr(l, mid, left) + asr(mid, r, right); //否则进一步递归
}
int main() {
double l, r;
scanf("%lf%lf", &l, &r);
printf("%lf\n", asr(l, r, simpson(l, r))); //自适应辛普森积分
return 0;
}
圆的面积并
给出 \(N\) 个圆,求其面积并。
输入格式
第一行一个整数 \(N\)。
接下来 \(N\) 行每行包含三个整数 \(x, y, r\),表示其中一个圆的圆心坐标为 \((x, y)\),半径为 \(r\)。
输出格式
输出一个实数,表示面积并。
输出结果与标准答案的绝对误差在 \(10^{-2}\) 以内,即视为正确。
输入样例
3
0 0 1000
1 0 1000
2 0 1000
输出样例
3145592.653
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 1010;
const double eps = 1e-8, INF = 1e9;
int n;
vector<PDD> segs; //存储所有包含圆的横坐标区间
struct Circle {
PDD r; //圆心
double R; //半径
}c[N]; //存储所有圆
PDD q[N]; //存储当前所有竖线上的区间
int dcmp(double x, double y) { //比较函数
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
void rotate(PDD& p, double angle) { //旋转一个角度
p = PDD(p.x * cos(angle) + p.y * sin(angle), -p.x * sin(angle) + p.y * cos(angle));
}
double f(double x) { //设 f(x0) 表示 x = x0 和所有圆的交集的长度
int cnt = 0;
for (int i = 0; i < n; i ++ ) {
auto X = fabs(x - c[i].r.x), R = c[i].R;
if (dcmp(X, R) < 0) { //如果第 i 个圆和 x = x0 有交集
auto Y = sqrt(R * R - X * X);
q[cnt ++ ] = {c[i].r.y - Y, c[i].r.y + Y};
}
}
if (!cnt) return 0; //如果没有交集,直接返回 0
sort(q, q + cnt); //将所有区间从小到大排序
double res = 0, st = q[0].x, ed = q[0].y; //记录并集的长度
for (int i = 1; i < cnt; i ++ ) //区间合并
if (q[i].x <= ed) ed = max(ed, q[i].y);
else {
res += ed - st;
st = q[i].x, ed = q[i].y;
}
return res + ed - st;
}
double simpson(double l, double r) { //求 [l, r] 内的近似面积
auto mid = (l + r) / 2;
return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}
double asr(double l, double r, double s) { //自适应辛普森积分,s 表示 [l, r] 区间内的近似面积
auto mid = (l + r) / 2;
auto left = simpson(l, mid), right = simpson(mid, r); //计算左、右区间的近似面积
if (fabs(s - left - right) < eps) return left + right; //如果误差足够小,直接返回
return asr(l, mid, left) + asr(mid, r, right); //否则继续递归
}
void merge() { // 区间合并
sort(segs.begin(), segs.end()); //将所有区间排序
vector<PDD> new_segs;
double l = -INF, r = -INF;
for (auto& seg: segs) {
if (dcmp(seg.x, r) <= 0) r = max(r, seg.y); //区间合并
else {
if (dcmp(l, -INF)) new_segs.push_back({l, r});
l = seg.x, r = seg.y;
}
}
new_segs.push_back({l, r});
segs = new_segs;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) {
scanf("%lf%lf%lf", &c[i].r.x, &c[i].r.y, &c[i].R);
rotate(c[i].r, 1); // 旋转一个随机角度
segs.push_back({c[i].r.x - c[i].R, c[i].r.x + c[i].R}); //将所有圆的横坐标区间存储起来
}
merge(); //将所有横坐标区间合并
double res = 0; //记录面积并
for (auto& seg: segs)
res += asr(seg.x, seg.y, simpson(seg.x, seg.y));
printf("%.3lf\n", res);
return 0;
}
全家桶
#include<algorithm>
#include<cstdio>
#include<cmath>
/*一:【准备工作】*/
#define LD double
#define LL long long
#define Re register int
#define Vector Point
using namespace std;
const int N=262144+3;
const LD eps=1e-8,Pi=acos(-1.0);
inline int dcmp(LD a){return a<-eps?-1:(a>eps?1:0);}//处理精度
inline LD Abs(LD a){return a*dcmp(a);}//取绝对值
struct Point{
LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
inline void in(){scanf("%lf%lf",&x,&y);}
inline void out(){printf("%.2lf %.2lf\n",x,y);}
};
/*二:【向量】*/
inline LD Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}//【点积】
inline LD Cro(Vector a,Vector b){return a.x*b.y-a.y*b.x;}//【叉积】
inline LD Len(Vector a){return sqrt(Dot(a,a));}//【模长】
inline LD Angle(Vector a,Vector b){return acos(Dot(a,b)/Len(a)/Len(b));}//【两向量夹角】
inline Vector Normal(Vector a){return Vector(-a.y,a.x);}//【法向量】
inline Vector operator+(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
inline Vector operator-(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
inline Vector operator*(Vector a,LD b){return Vector(a.x*b,a.y*b);}
inline bool operator==(Point a,Point b){return !dcmp(a.x-b.x)&&!dcmp(a.y-b.y);}//两点坐标重合则相等
/*三:【点、向量的位置变换】*/
/*1.【点、向量的旋转】*/
inline Point turn_P(Point a,LD theta){//【点A\向量A顺时针旋转theta(弧度)】
LD x=a.x*cos(theta)+a.y*sin(theta);
LD y=-a.x*sin(theta)+a.y*cos(theta);
return Point(x,y);
}
inline Point turn_PP(Point a,Point b,LD theta){//【将点A绕点B顺时针旋转theta(弧度)】
LD x=(a.x-b.x)*cos(theta)+(a.y-b.y)*sin(theta)+b.x;
LD y=-(a.x-b.x)*sin(theta)+(a.y-b.y)*cos(theta)+b.y;
return Point(x,y);
}
/*四:【图形与图形之间的关系】*/
/*1.【点与线段】*/
inline int pan_PL(Point p,Point a,Point b){//【判断点P是否在线段AB上】
return !dcmp(Cro(p-a,b-a))&&dcmp(Dot(p-a,p-b))<=0;//做法一
// return !dcmp(Cro(p-a,b-a))&&dcmp(min(a.x,b.x)-p.x)<=0&&dcmp(p.x-max(a.x,b.x))<=0&&dcmp(min(a.y,b.y)-p.y)<=0&&dcmp(p.y-max(a.y,b.y))<=0;//做法二
//PA,AB共线且P在AB之间(其实也可以用len(p-a)+len(p-b)==len(a-b)判断,但是精度损失较大)
}
inline LD dis_PL(Point p,Point a,Point b){//【点P到线段AB距离】
if(a==b)return Len(p-a);//AB重合
Vector x=p-a,y=p-b,z=b-a;
if(dcmp(Dot(x,z))<0)return Len(x);//P距离A更近
if(dcmp(Dot(y,z))>0)return Len(y);//P距离B更近
return Abs(Cro(x,z)/Len(z));//面积除以底边长
}
/*2.【点与直线】*/
inline int pan_PL_(Point p,Point a,Point b){//【判断点P是否在直线AB上】
return !dcmp(Cro(p-a,b-a));//PA,AB共线
}
inline Point FootPoint(Point p,Point a,Point b){//【点P到直线AB的垂足】
Vector x=p-a,y=p-b,z=b-a;
LD len1=Dot(x,z)/Len(z),len2=-1.0*Dot(y,z)/Len(z);//分别计算AP,BP在AB,BA上的投影
return a+z*(len1/(len1+len2));//点A加上向量AF
}
inline Point Symmetry_PL(Point p,Point a,Point b){//【点P关于直线AB的对称点】
return p+(FootPoint(p,a,b)-p)*2;//将PF延长一倍即可
}
/*3.【线与线】*/
inline Point cross_LL(Point a,Point b,Point c,Point d){//【两直线AB,CD的交点】
Vector x=b-a,y=d-c,z=a-c;
return a+x*(Cro(y,z)/Cro(x,y));//点A加上向量AF
}
inline int pan_cross_L_L(Point a,Point b,Point c,Point d){//【判断直线AB与线段CD是否相交】
return pan_PL(cross_LL(a,b,c,d),c,d);//直线AB与直线CD的交点在线段CD上
}
inline int pan_cross_LL(Point a,Point b,Point c,Point d){//【判断两线段AB,CD是否相交】
LD c1=Cro(b-a,c-a),c2=Cro(b-a,d-a);
LD d1=Cro(d-c,a-c),d2=Cro(d-c,b-c);
return dcmp(c1)*dcmp(c2)<0&&dcmp(d1)*dcmp(d2)<0;//分别在两侧
}
/*4.【点与多边形】*/
inline int PIP(Point *P,Re n,Point a){//【射线法】判断点A是否在任意多边形Poly以内
Re cnt=0;LD tmp;
for(Re i=1;i<=n;++i){
Re j=i<n?i+1:1;
if(pan_PL(a,P[i],P[j]))return 2;//点在多边形上
if(a.y>=min(P[i].y,P[j].y)&&a.y<max(P[i].y,P[j].y))//纵坐标在该线段两端点之间
tmp=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x),cnt+=dcmp(tmp-a.x)>0;//交点在A右方
}
return cnt&1;//穿过奇数次则在多边形以内
}
inline int judge(Point a,Point L,Point R){//判断AL是否在AR右边
return dcmp(Cro(L-a,R-a))>0;//必须严格以内
}
inline int PIP_(Point *P,Re n,Point a){//【二分法】判断点A是否在凸多边形Poly以内
//点按逆时针给出
if(judge(P[1],a,P[2])||judge(P[1],P[n],a))return 0;//在P[1_2]或P[1_n]外
if(pan_PL(a,P[1],P[2])||pan_PL(a,P[1],P[n]))return 2;//在P[1_2]或P[1_n]上
Re l=2,r=n-1;
while(l<r){//二分找到一个位置pos使得P[1]_A在P[1_pos],P[1_(pos+1)]之间
Re mid=l+r+1>>1;
if(judge(P[1],P[mid],a))l=mid;
else r=mid-1;
}
if(judge(P[l],a,P[l+1]))return 0;//在P[pos_(pos+1)]外
if(pan_PL(a,P[l],P[l+1]))return 2;//在P[pos_(pos+1)]上
return 1;
}
/*5.【线与多边形】*/
/*6.【多边形与多边形】*/
inline int judge_PP(Point *A,Re n,Point *B,Re m){//【判断多边形A与多边形B是否相离】
for(Re i1=1;i1<=n;++i1){
Re j1=i1<n?i1+1:1;
for(Re i2=1;i2<=m;++i2){
Re j2=i2<m?i2+1:1;
if(pan_cross_LL(A[i1],A[j1],B[i2],B[j2]))return 0;//两线段相交
if(PIP(B,m,A[i1])||PIP(A,n,B[i2]))return 0;//点包含在内
}
}
return 1;
}
/*五:【图形面积】*/
/*1.【任意多边形面积】*/
inline LD PolyArea(Point *P,Re n){//【任意多边形P的面积】
LD S=0;
for(Re i=1;i<=n;++i)S+=Cro(P[i],P[i<n?i+1:1]);
return S/2.0;
}
/*2.【圆的面积并】*/
/*3.【三角形面积并】*/
/*六:【凸包】*/
/*1.【求凸包】*/
inline bool cmp1(Vector a,Vector b){return a.x==b.x?a.y<b.y:a.x<b.x;};//按坐标排序
inline int ConvexHull(Point *P,Re n,Point *cp){//【水平序Graham扫描法(Andrew算法)】求凸包
sort(P+1,P+n+1,cmp1);
Re t=0;
for(Re i=1;i<=n;++i){//下凸包
while(t>1&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
Re St=t;
for(Re i=n-1;i>=1;--i){//上凸包
while(t>St&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
return --t;//要减一
}
/*2.【旋转卡壳】*/
/*3.【半平面交】*/
struct Line{
Point a,b;LD k;Line(Point A=Point(0,0),Point B=Point(0,0)){a=A,b=B,k=atan2(b.y-a.y,b.x-a.x);}
inline bool operator<(const Line &O)const{return dcmp(k-O.k)?dcmp(k-O.k)<0:judge(O.a,O.b,a);}//如果角度相等则取左边的
}L[N],Q[N];
inline Point cross(Line L1,Line L2){return cross_LL(L1.a,L1.b,L2.a,L2.b);}//获取直线L1,L2的交点
inline int judge(Line L,Point a){return dcmp(Cro(a-L.a,L.b-L.a))>0;}//判断点a是否在直线L的右边
inline int halfcut(Line *L,Re n,Point *P){//【半平面交】
sort(L+1,L+n+1);Re m=n;n=0;
for(Re i=1;i<=m;++i)if(i==1||dcmp(L[i].k-L[i-1].k))L[++n]=L[i];
Re h=1,t=0;
for(Re i=1;i<=n;++i){
while(h<t&&judge(L[i],cross(Q[t],Q[t-1])))--t;//当队尾两个直线交点不是在直线L[i]上或者左边时就出队
while(h<t&&judge(L[i],cross(Q[h],Q[h+1])))++h;//当队头两个直线交点不是在直线L[i]上或者左边时就出队
Q[++t]=L[i];
}
while(h<t&&judge(Q[h],cross(Q[t],Q[t-1])))--t;
while(h<t&&judge(Q[t],cross(Q[h],Q[h+1])))++h;
n=0;
for(Re i=h;i<=t;++i)P[++n]=cross(Q[i],Q[i<t?i+1:h]);
return n;
}
/*4.【闵可夫斯基和】*/
Vector V1[N],V2[N];
inline int Mincowski(Point *P1,Re n,Point *P2,Re m,Vector *V){//【闵可夫斯基和】求两个凸包{P1},{P2}的向量集合{V}={P1+P2}构成的凸包
for(Re i=1;i<=n;++i)V1[i]=P1[i<n?i+1:1]-P1[i];
for(Re i=1;i<=m;++i)V2[i]=P2[i<m?i+1:1]-P2[i];
Re t=0,i=1,j=1;V[++t]=P1[1]+P2[1];
while(i<=n&&j<=m)++t,V[t]=V[t-1]+(dcmp(Cro(V1[i],V2[j]))>0?V1[i++]:V2[j++]);
while(i<=n)++t,V[t]=V[t-1]+V1[i++];
while(j<=m)++t,V[t]=V[t-1]+V2[j++];
return t;
}
/*5.【动态凸包】*/
/*七:【圆】*/
/*1.【三点确定一圆】*/
#define S(a) ((a)*(a))
struct Circle{Point O;LD r;Circle(Point P,LD R=0){O=P,r=R;}};
inline Circle getCircle(Point A,Point B,Point C){//【三点确定一圆】暴力解方程
LD x1=A.x,y1=A.y,x2=B.x,y2=B.y,x3=C.x,y3=C.y;
LD D=((S(x2)+S(y2)-S(x3)-S(y3))*(y1-y2)-(S(x1)+S(y1)-S(x2)-S(y2))*(y2-y3))/((x1-x2)*(y2-y3)-(x2-x3)*(y1-y2));
LD E=(S(x1)+S(y1)-S(x2)-S(y2)+D*(x1-x2))/(y2-y1);
LD F=-(S(x1)+S(y1)+D*x1+E*y1);
return Circle(Point(-D/2.0,-E/2.0),sqrt((S(D)+S(E)-4.0*F)/4.0));
}
inline Circle getcircle(Point A,Point B,Point C){//【三点确定一圆】向量垂心法
Point P1=(A+B)*0.5,P2=(A+C)*0.5;
Point O=cross_LL(P1,P1+Normal(B-A),P2,P2+Normal(C-A));
return Circle(O,Len(A-O));
}
/*2.【最小覆盖圆】*/
inline int PIC(Circle C,Point a){return dcmp(Len(a-C.O)-C.r)<=0;}//判断点A是否在圆C内
inline void Random(Point *P,Re n){for(Re i=1;i<=n;++i)swap(P[i],P[rand()%n+1]);}//随机一个排列
inline Circle Min_Circle(Point *P,Re n){//【求点集P的最小覆盖圆】
// random_shuffle(P+1,P+n+1);
Random(P,n);Circle C=Circle(P[1],0);
for(Re i=2;i<=n;++i)if(!PIC(C,P[i])){
C=Circle(P[i],0);
for(Re j=1;j<i;++j)if(!PIC(C,P[j])){
C.O=(P[i]+P[j])*0.5,C.r=Len(P[j]-C.O);
for(Re k=1;k<j;++k)if(!PIC(C,P[k]))C=getcircle(P[i],P[j],P[k]);
}
}
return C;
}
/*3.【三角剖分】*/
inline LD calc(Point A,Point B,Point O,LD R){//【三角剖分】
if(A==O||B==O)return 0;
Re op=dcmp(Cro(A-O,B-O))>0?1:-1;LD ans=0;
Vector x=A-O,y=B-O;
Re flag1=dcmp(Len(x)-R)>0,flag2=dcmp(Len(y)-R)>0;
if(!flag1&&!flag2)ans=Abs(Cro(A-O,B-O))/2.0;//两个点都在里面
else if(flag1&&flag2){//两个点都在外面
if(dcmp(dis_PL(O,A,B)-R)>=0)ans=R*R*Angle(x,y)/2.0;//完全包含了圆弧
else{//分三段处理 △+圆弧+△
if(dcmp(Cro(A-O,B-O))>0)swap(A,B);//把A换到左边
Point F=FootPoint(O,A,B);LD lenx=Len(F-O),len=sqrt(R*R-lenx*lenx);
Vector z=turn_P(F-O,Pi/2.0)*(len/lenx);Point B_=F+z,A_=F-z;
ans=R*R*(Angle(A-O,A_-O)+Angle(B-O,B_-O))/2.0+Cro(B_-O,A_-O)/2.0;
}
}
else{//一个点在里面,一个点在外面
if(flag1)swap(A,B);//使A为里面的点,B为外面的点
Point F=FootPoint(O,A,B);LD lenx=Len(F-O),len=sqrt(R*R-lenx*lenx);
Vector z=turn_P(F-O,Pi/2.0)*(len/lenx);Point C=dcmp(Cro(A-O,B-O))>0?F-z:F+z;
ans=Abs(Cro(A-O,C-O))/2.0+R*R*Angle(C-O,B-O)/2.0;
}
return ans*op;
}
int main(){}
数据结构
单链表
int head, e[N], ne[N], idx;
// 初始化
void init() {
head = -1;
idx = 0;
}
// 向链表头插入一个数
void add_to_head(int x) {
e[idx] = x, ne[idx] = head, head = idx ++ ;
}
// 在第 k 个插入的数后插入一个数
void add(int k, int x) {
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}
// 删除第 k 个插入的数后面的一个数
void remove(int k) {
ne[k] = ne[ne[k]];
}
操作说明
- 向链表头插入一个数:
add_to_head(x);
- 删除第 k 个插入的数后面的一个数:
if (!k) head = ne[head];
else remove(k - 1);
- 在第 k 个插入的数后插入一个数:
add(k - 1, x);
双链表
int e[N], l[N], r[N], idx;
// 初始化
void init() {
r[0] = 1, l[1] = 0;
idx = 2;
}
// 在节点a的右边插入一个数x
void insert(int a, int x) {
e[idx] = x;
l[idx] = a, r[idx] = r[a];
l[r[a]] = idx, r[a] = idx ++ ;
}
// 删除节点a
void remove(int a) {
l[r[a]] = l[a];
r[l[a]] = r[a];
}
操作说明
- 在链表的最左端插入数 x:
insert(0, x);
- 在链表的最右端插入数x:
insert(l[1], x);
- 将第k个插入的数删除:
remove(k + 1);
- 在第k个插入的数左边插入一个数:
insert(l[k + 1], x);
- 在第k个插入的数右边插入一个数:
insert(k + 1, x);
单调栈
说明
查找每个数左边第一个比它小的数,不存在输出 -1
//参考代码
while (tt && stk[tt] >= x) tt -- ; //保证栈顶元素小于x
if (!tt) printf("-1 ");
else printf("%d ", stk[tt]);
stk[ ++ tt] = x;
单调队列
滑动窗口:该数组为 [1 3 -1 -3 5 3 6 7],k 为 3。
| 窗口位置 | 最小值 | 最大值 |
|---|---|---|
| [1 3 -1] -3 5 3 6 7 | -1 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | -3 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | -3 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | -3 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | 3 | 6 |
| 1 3 -1 -3 5 [3 6 7] | 3 | 7 |
最大值
int hh = 0, tt = -1; //队列左端点和右端点
for (int i = 0; i < n; i ++ ) {
if (hh <= tt && q[hh] <= i - k) hh ++ ; //判断左端点元素是否划出去了
while (hh <= tt && a[i] >= a[q[tt]]) tt --; //保证最大值
q[ ++ tt] = i;
if (i >= k - 1) cout << a[q[hh]] << ' '; //只有长度大于等于k的时候才进行输出
}
最小值
int hh = 0, tt = -1; //队列左端点和右端点
for (int i = 0; i < n; i ++ ) {
if (hh <= tt && q[hh] <= i - k) hh ++ ; //判断左端点元素是否划出去了
while (hh <= tt && a[i] <= a[q[tt]]) tt -- ; //保证最小值
q[ ++ tt] = i;
if (i >= k - 1) cout << a[q[hh]] << ' '; //只有长度大于等于k的时候才进行输出
}
KMP
说明
通过预处理,可以求出 \(P\) 在 \(S\) 中所有出现的位置的起始下标
int n, m; //m是S的长度,n是P的长度
int ne[N];
char s[M], p[N]; //S为模板,P为目标
for (int i = 2, j = 0; i <= n; i ++ ) { //预处理
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
for (int i = 1, j = 0; i <= m; i ++ ) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == n) {
cout << i - n << ' '; //出现的下标位置
j = ne[j];
}
}
Tire树
int n;
int q[N][26], cnt[N], idx; //cnt记录个数
char s[N];
void insert(char s[]) {
int p = 0;
for(int i = 0; s[i]; i ++ ) {
int c = s[i] - 'a';
if(!q[p][c]) q[p][c] = ++ idx;
p = q[p][c];
}
cnt[p] ++ ;
}
int find(char s[]) {
int p = 0;
for(int i = 0; s[i]; i++)
{
int c = s[i] - 'a';
if(!q[p][c]) return 0;
p = q[p][c];
}
return cnt[p];
}
操作说明
- 向集合中插入一个字符串 \(s\):
insert(s);
- 询问一个字符串在集合中出现了多少次:
find(s);
可持久化Trie
说明
参考代码为求取最大异或和的模板
给定一个非负整数序列 \(a\),初始长度为 \(N\)。
有 \(M\) 个操作,有以下两种操作类型:
A x:添加操作,表示在序列末尾添加一个数 \(x\),序列的长度 \(N\) 增大 \(1\)。Q l r x:询问操作,你需要找到一个位置 \(p\),满足 \(l≤p≤r\),使得:\(a[p]\ xor\ a[p+1]\ xor\ … \ xor\ a[N]\ xor\ x\) 最大,输出这个最大值。
输入格式
第一行包含两个整数 \(N,M\),含义如问题描述所示。
第二行包含 \(N\) 个非负整数,表示初始的序列 \(A\)。
接下来 \(M\) 行,每行描述一个操作,格式如题面所述。
输出格式
每个询问操作输出一个整数,表示询问的答案。
每个答案占一行。
输入样例
5 5
2 6 4 3 6
A 1
Q 3 5 4
A 4
Q 5 7 0
Q 3 6 6
输出样例
4
5
6
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 10, M = 25 * N;
int n, m;
int tr[M][2], max_id[M]; //用于记录当前根节点版本的最大id范围,也就是当前节点对应的s的位置
int root[N], idx;
int s[N]; //前缀和序列
//i是第i个插入的数i,p是上一个插入的数的节点号,q是当前节点号,k是现在取到第k位
void insert(int i, int k, int p, int q) {
if (k < 0) { //如果记录结束了
max_id[q] = i; //记录当前节点所能到达的最大范围i
return;
}
int v = s[i] >> k & 1; //取出当前需要的二进制位
if (p) tr[q][v ^ 1] = tr[p][v ^ 1]; //如果前一个节点存在当前节点没有分支,那么就指向前一个空节点
tr[q][v] = ++ idx; //trie树插入
insert(i, k - 1, tr[p][v], tr[q][v]); //递归下一位
max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]);
}
int query(int root, int C, int L) { //L为限制,L~root之间的版本是符合要求的,C为匹配的目标值
int p = root;
for (int i = 23; i >= 0; i -- ) {
int v = C >> i & 1;
if (max_id[tr[p][v ^ 1]] >= L) {
p = tr[p][v ^ 1];
} else {
p = tr[p][v];
}
}
return C ^ s[max_id[p]];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
max_id[0] = -1; //初始化
root[0] = ++ idx;
insert(0, 23, 0, root[0]);
for (int i = 1; i <= n; i ++ ) {
int x;
cin >> x;
root[i] = ++ idx;
s[i] = s[i - 1] ^ x;
insert(i, 23, root[i - 1], root[i]);
}
string op;
int l, r, x;
while (m -- ) {
cin >> op;
if (op == "A") { //操作1
cin >> x;
n ++ ;
s[n] = s[n - 1] ^ x; //前缀和
root[n] = ++ idx; //初始化root
insert(n, 23, root[n - 1], root[n]); //插入
} else { //操作2
cin >> l >> r >> x;
cout << query(root[r - 1], s[n] ^ x, l - 1) << endl; //查询
}
}
return 0;
}
并查集
带权并查集
给定一个包含 \(n\) 个点(编号为 \(1∼n\))的无向图,初始时图中没有边。
现在要进行 \(m\) 个操作,操作共有三种:
C a b,在点 \(a\) 和点 \(b\) 之间连一条边,\(a\) 和 \(b\) 可能相等;Q1 a b,询问点 \(a\) 和点 \(b\) 是否在同一个连通块中,\(a\) 和 \(b\) 可能相等;Q2 a,询问点 \(a\) 所在连通块中点的数量;
输入格式
第一行输入整数 \(n\) 和 \(m\)。
接下来 \(m\) 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 \(a\) 和 \(b\) 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 \(a\) 所在连通块中点的数量
每个结果占一行。
输入样例
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例
Yes
2
3
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int p[N];
int cnt[N];
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) { //初始化
p[i] = i;
cnt[i] = 1;
}
string op;
int x, y;
while (m -- ) {
cin >> op;
if(op == "C") {
cin >> x >> y;
x = find(x), y = find(y);
if(x != y) { //如果不在一个集合内,就合并
p[x] = y;
cnt[y] += cnt[x];
}
} else if(op=="Q1") {
cin >> x >> y;
x = find(x), y = find(y);
if(x == y) puts("Yes");
else puts("No");
} else {
cin >> x;
x = find(x);
cout << cnt[x] << endl;
}
}
return 0;
}
扩展域并查集
第一行包含一个整数 \(N\),表示 01 序列长度。
第二行包含一个整数 \(M\),表示问题数量。
接下来 \(M\) 行,每行包含一组问答:两个整数 \(l\) 和 \(r\),以及回答 even 或 odd,用以描述 \(S[l∼r]\) 中有偶数个 1 还是奇数个 1。
输出一个整数 \(k\),表示 \(01\) 序列满足第 \(1∼k\) 个回答,但不满足第 \(1∼k+1\) 个回答,如果 \(01\) 序列满足所有回答,则输出问题总数量。
输入样例
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd
输出样例
3
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e4 + 10, Base = N / 2; //Base为扩展域用法
int n, m;
int p[N];
unordered_map<int, int> S;
int get(int x) { //离散化
if (S.count(x) == 0) S[x] = ++ n; //不存在就新建
return S[x];
}
int find(int x) { //并查集
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main() {
cin >> n >> m;
n = 0;
for (int i = 0; i < N; i ++ ) p[i] = i;
int res = m;
for (int i = 1; i <= m; i ++ ) {
int a, b;
string type;
cin >> a >> b >> type;
a = get(a - 1), b = get(b);
if (type == "even") {
if (find(a) == find(b + Base)) { //如果a和b一奇一偶,说明有问题
res = i - 1;
break;
}
p[find(a)] = find(b); //同奇
p[find(a + Base)] = find(b + Base); //同偶
} else {
if (find(a) == find(b)) { //奇偶相同有问题
res = i - 1;
break;
}
p[find(a)] = find(b + Base);
p[find(a + Base)] = find(b);
}
}
cout << res << endl;
return 0;
}
堆
void heap_swap(int a, int b) { //交换heap中位置分别为a, b的两个元素
swap(ph[hp[a]], ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u) { //下沉
int t = u;
if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u) { //上浮
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
操作说明
- 插入一个数 \(x\):
cnt ++ ; //堆中元素个数
m ++ ; //第m个数
ph[m] = cnt, hp[cnt] = m;
h[cnt] = x;
up(cnt);
- 输出当前集合中的最小值:
cout << h[1] << endl;
- 删除当前集合中的最小值(数据保证此时的最小值唯一):
heap_swap(1, cnt);
cnt -- ;
down(1);
- 删除第 \(k\) 个插入的数:
k = ph[k];
heap_swap(k, cnt);
cnt -- ;
up(k);
down(k);
- 修改第 \(k\) 个插入的数,将其变为 \(x\) :
k = ph[k];
h[k] = x;
up(k);
down(k);
哈希表
手写哈希
拉链法
const int N = 100003;
int h[N], e[N], ne[N], idx;
void init() { //初始化
memset(h, -1, sizeof h);
idx = 0;
}
void insert(int x) { //插入x
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
bool find(int x) { //查询x是否存在
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
开放寻址法
const int N = 200003, null = 0x3f3f3f3f;
int h[N];
void init() { //初始化
memset(h, 0x3f, sizeof h);
}
int find(int x) { //如果x在哈希表中存在,返回x的下标,如果不在,则返回x应插入的位置
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
操作说明
- 插入 \(x\) :
h[find(x)] = x;
- 询问 \(x\) 是否出现过:
if (h[find(x)] == null) cout << "No" << endl;
else cout << "Yes" << endl;
字符串哈希
将字符串看成P进制数,P一般为131或13331,冲突概率低
typedef unsigned long long ULL;
const int N = 100010, P = 131; //特殊的P
int n, m;
char str[N]; //下标从1开始
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
void init() {
p[0] = 1;
for (int i = 1; i <= n; i ++ ) {
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
}
ULL get(int l, int r) { //返回一段的哈希值
return h[r] - h[l - 1] * p[r - l + 1];
}
判断两个区间是否相同:
if (get(l1, r1) == get(l2, r2)) cout << "Yes" << endl;
else cout << "No" << endl;
区间集合查询
- 说明:查询指定区间的集合是否相同(集合内的数或字母,在排序后完全相同)
#include <bits/stdc++.h> //参考代码,非模板。
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
int main() {
int n, q; //数组长度为n,q次询问。
cin >> n >> q;
LL p[200010] = {};
for (int i = 0; i < 200005; i ++ ) p[i] = (998244353 + (LL) rand() * rand() * rand()) % 998244353; //给每个数定义一个哈希值
int A[200010], B[200010]; //需要进行匹配的两个数组
for (int i = 1; i <= n; i ++ ) cin >> A[i];
for (int i = 1; i <= n; i ++ ) cin >> B[i];
LL C[200010] = {};
LL D[200010] = {};
for (int i = 1; i <= n; i ++ ) {
C[i] = C[i - 1] + p[A[i]]; //对原数组进行哈希处理。
D[i] = D[i - 1] + p[B[i]];
}
while (q -- ) {
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if (r1 - l1 != r2 - l2) {
cout << "No" << endl;
continue;
}
LL a = C[r1] - C[l1 - 1]; //前缀和查找
LL b = D[r2] - D[l2 - 1];
if (a == b) cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}
树状数组
给定长度为 \(N\) 的数列 \(A\),然后输入 \(M\) 行操作指令。
第一类指令形如 C l r d,表示把数列中第 \(l∼r\) 个数都加 \(d\) 。
第二类指令形如 Q x,表示询问数列中第 \(x\) 个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
输入样例
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例
4
1
2
5
类型说明:区间修改,单点查询
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
int a[N]; //原数组
LL tr[N]; //树状数组
int lowbit(int x) {
return x & -x;
}
void add(int x, int c) { //修改
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
LL sum (int x) { //查询
LL res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
cin >> a[i];
}
for (int i = 1; i <= n; i ++ ) {
add(i, a[i] - a[i - 1]); //差分
}
string op;
int l, r, d;
while (m -- ) {
cin >> op;
if (op == "Q") { //查询
cin >> d;
cout << sum(d) << endl;
} else { //修改
cin >> l >> r >> d;
add(l, d); //左加
add(r + 1, -d); //右减
}
}
return 0;
}
线段树
给定一个长度为 \(N\) 的数列 \(A\),以及 \(M\) 条指令,每条指令可能是以下两种之一:
C l r d,表示把 \(A[l],A[l+1],…,A[r]\) 都加上 \(d\)。Q l r,表示询问数列中第 \(l∼r\) 个数的和。
对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数 \(N,M\)。
第二行 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
输入样例
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例
4
55
9
15
类型说明:区间修改,区间查询
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
int w[N];
//本写法的懒标记为:当前区间已运算过,所有子区间并未进行运算
struct Node {
int l, r; //左右区间
LL sum, add; //区间和,懒标记
}tr[N * 4]; //线段树数组
void pushup(int u) { //上传
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u) { //下沉
auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if (root.add) {
left.add += root.add; right.add += root.add; //懒标记下传
left.sum += (LL)(left.r - left.l + 1) * root.add;
right.sum += (LL)(right.r - right.l + 1) * root.add;
root.add = 0;
}
}
void build(int u, int l, int r) { //建立
tr[u] = {l, r};
if (l == r) {
tr[u].sum = w[l];
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid); //左半边
build(u << 1 | 1, mid + 1, r); //右半边
pushup(u);
}
void modify(int u, int l, int r, int d) { //区间求改
if (l <= tr[u].l && tr[u].r <= r) {
tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
tr[u].add += d;
} else {
pushdown(u); //先下沉
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, d); //需要修改左半边
if (r > mid) modify(u << 1 | 1, l, r, d); //需要修改右半边
pushup(u); //再上传
}
}
LL query(int u, int l, int r) {
if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum; //在目标区间内,直接返回
pushdown(u);
LL sum = 0;
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) sum += query(u << 1, l, r); //同修改
if (r > mid) sum += query(u << 1 | 1, l, r);
return sum;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
cin >> w[i];
}
build(1, 1, n);
string op;
int l, r, d;
while (m -- ) {
cin >> op;
if (op == "Q") { //查询
cin >> l >> r;
cout << query(1, l, r) << endl;
} else { //区间修改
cin >> l >> r >> d;
modify(1, l, r, d);
}
}
return 0;
}
主席树
给定长度为 \(N\) 的整数序列 \(A\),下标为 \(1∼N\)。
现在要执行 \(M\) 次操作,其中第 \(i\) 次操作为给出三个整数 \(l_i,r_i,k_i\) 求 \(A[l_i],A[l_i+1],…,A[r_i]\) (即 \(A\) 的下标区间 \([l_i,r_i]\))中第 \(k_i\) 小的数是多少。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含 \(N\) 个整数,表示整数序列 \(A\)。
接下来 \(M\) 行,每行包含三个整数 \(li,ri,ki\),用以描述第 \(i\) 次操作。
输出格式
对于每次操作输出一个结果,表示在该次操作中,第 \(k\) 小的数的数值。
每个结果占一行。
输入样例
7 3
1 5 2 6 3 7 4
2 5 3
4 4 1
1 7 3
输出样例
5
6
3
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct Node {
int l, r; //分别表示左右节点
int cnt; //表示当前树节点插入了多少个数
}tr[N * 4 + N * 17]; //初始骨架N * 4 再加上最多M次插入一共修改MlogM个节点
int n, m;
int root[N], idx; //root记录根节点的版本号【root[r]表示插入了第r个数版本的线段树】, idx记录树节点的版本号
int a[N]; //原始数组
vector<int> nums; //离散化
int find(int x) { //查询离散化后的下标
return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}
int build(int l, int r) { //返回标志值
int p = ++ idx;
if (l == r) return p; //到叶子节点了
int mid = l + r >> 1;
//递归到最底层之后向上给父节点的属性赋值
tr[p].l = build(l, mid);
tr[p].r = build(mid + 1, r);
return p;
}
// l, r是要放入的坐标范围, x是要插入的数离散化后的位置
int insert(int p, int l, int r, int x) { //返回值是新版本树节点的标志值
int q = ++ idx;
tr[q] = tr[p]; //先将上一个版本信息复制过来
if (l == r) { //遍历到叶子节点,同时找到了要插入的位置,cnt++
tr[q].cnt ++ ;
return q;
}
//接着找要插入的位置
int mid = l + r >> 1;
//这里也是新版本树节点直接复制旧版本树的信息,同时返回一个新的版本号
//下表小于mid放左区间,反之放右区间
if (x <= mid) tr[q].l = insert(tr[p].l, l, mid, x);
else tr[q].r = insert(tr[p].r, mid + 1, r, x);
tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;
return q;
}
// l ,r是检索范围, q是当前第r个节点root[r]能包含1~r之间所有
// q的输入是root[r],p的输入是root[l-1], 作用是剔除这个根节点所包含数据的影响(前缀和的思想)
int query(int q, int p, int l, int r, int k) {
//遍历到了叶子节点的位置,说明找到了所需要的位置
if (l == r) return r;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
int mid = l + r >> 1;
// k <= cnt说明要找的元素在q的左子树里面, 同时这里面也要剔除掉包含在p左子树的内容
if (k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
cin >> a[i];
nums.emplace_back(a[i]);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
root[0] = build(0, nums.size() - 1); //初始时,建立一个空的骨架,不同版本的线段树的结构都是一样的
for (int i = 1; i <= n; i ++ ) {
root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i]));
}
while (m -- ) {
int l, r, k;
cin >> l >> r >> k;
//查询[l,r]区间中的第k大数,利用前缀和的思想,从[l ~ r]中的数据剔除掉[1 ~ l-1]的数据,
//不同版本的线段树的结构都是一样的,所以初始都是从0到nums.size()这个范围当中找
cout << nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)] << endl;
}
return 0;
}
平衡树(treap)
输入样例
8
1 10
1 20
1 30
3 20
4 2
2 10
5 25
6 -1
输出样例
2
20
20
20
参考代码
const int N = 1e5 + 10, INF = 1e8;
struct Node {
int l, r;
int key, val;
int cnt, size;
}tr[N];
int n;
int root, idx;
void pushup(int p) { //上传
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}
int get_node(int key) { //获取x的节点编号
tr[++ idx].key = key;
tr[idx].val = rand();
tr[idx].cnt = tr[idx].size = 1;
return idx;
}
void zig(int &p) { //右旋
int q = tr[p].l;
tr[p].l = tr[q].r;
tr[q].r = p;
p = q;
pushup(tr[p].r);
pushup(p);
}
void zag(int &p) { //左旋
int q = tr[p].r;
tr[p].r = tr[q].l;
tr[q].l = p;
p = q;
pushup(tr[p].l);
pushup(p);
}
void build() { //建树
get_node(-INF), get_node(INF);
root = 1, tr[root].r = 2;
pushup(root);
if (tr[1].val < tr[2].val) zag(root);
}
void insert(int &p, int key) { //删除x
if (!p) p = get_node(key);
else if (tr[p].key == key) tr[p].cnt ++ ;
else if (tr[p].key > key) {
insert(tr[p].l, key);
if (tr[tr[p].l].val > tr[p].val) zig(p);
}
else {
insert(tr[p].r, key);
if (tr[tr[p].r].val > tr[p].val) zag(p);
}
pushup(p);
}
void remove(int &p, int key) { //删除x
if (!p) return;
if (tr[p].key == key) {
if (tr[p].cnt > 1) tr[p].cnt -- ;
else if (tr[p].l || tr[p].r) {
if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) {
zig(p);
remove(tr[p].r, key);
} else {
zag(p);
remove(tr[p].l, key);
}
} else {
p = 0;
}
} else if (tr[p].key > key) remove(tr[p].l, key);
else remove(tr[p].r, key);
pushup(p);
}
int get_rank_by_key(int p, int key) { //通过数值找排名
if (!p) return 0;
if (tr[p].key == key) return tr[tr[p].l].size + 1;
if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}
int get_key_by_rank(int p, int rank) { //通过排名找数值
if (!p) return INF;
if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);
if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}
int get_prev(int p, int key) { 找到严格小于key的最大数
if (!p) return -INF;
if (tr[p].key >= key) return get_prev(tr[p].l, key);
return max(tr[p].key, get_prev(tr[p].r, key));
}
int get_next(int p, int key) { 找到严格大于key的最小数
if (!p) return INF;
if (tr[p].key <= key) return get_next(tr[p].r, key);
return min(tr[p].key, get_next(tr[p].l, key));
}
操作说明
- 插入数值 \(x\):
insert(root, x);
- 删除数值 \(x\) (若有多个相同的数, 应只删除一个):
remove(root, x);
- 查询数值 \(x\) 的排名(若有多个相同的数,应输出最小的排名):
get_rank_by_key(root, x) - 1;
- 查询排名为 \(x\) 的数值:
get_key_by_rank(root, x + 1);
- 求数值 \(x\) 的前驱(前驱定义为小于 \(x\) 的最大的数):
get_prev(root, x);
- 求数值 \(x\) 的后继(后继定义为大于 \(x\) 的最小的数):
get_next(root, x);
AC自动机
搜索关键词
给定 \(n\) 个长度不超过 \(50\) 的由小写英文字母组成的单词,以及一篇长为 \(m\) 的文章。
请问,其中有多少个单词在文章中出现了。
注意:每个单词不论在文章中出现多少次,仅累计 \(1\) 次。
数据范围
$1 \le n \le 10^4 $ \(1 \le m \le 10^6\)
输入样例
5
she
he
say
shr
her
yasherhs
输出样例
3
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, S = 55;
int n;
int tr[N * S][26], cnt[N * S], idx; //cnt[i]表示以i+'a'为结尾的个数,idx为当前节点的指针
char str[1000010]; //以"\0"结尾
int ne[N * S];
void init() {
memset(tr, 0, sizeof tr);
memset(cnt, 0, sizeof cnt);
memset(ne, 0, sizeof ne);
idx = 0;
}
void insert() {
int p = 0;
for (int i = 0; str[i]; i ++ ) {
int t = str[i] - 'a'; //第t个儿子
if (!tr[p][t]) tr[p][t] = ++ idx; //没有这个儿子就建立它,注意要++idx,防止和根节点的0重复
p = tr[p][t];
}
cnt[p] ++ ;
}
void build() {
queue<int> q;
for (int i = 0; i < 26; i ++ ) {
if (tr[0][i]) {
q.push(tr[0][i]);
}
}
while (q.size()) {
int t = q.front();
q.pop();
for (int i = 0; i < 26; i ++ ) {
int p = tr[t][i];
if (!p) tr[t][i] = tr[ne[t]][i];
else {
ne[p] = tr[ne[t]][i];
q.push(p);
}
}
}
}
int main() {
init();
cin >> n;
while (n -- ) {
cin >> str;
insert();
}
build();
cin >> str;
int res = 0;
//j记录当前树节点的指针,初始是根节点
for (int i = 0, j = 0; str[i]; i ++ ) { //枚举总串str的每一个字母
int t = str[i] - 'a';
j = tr[j][t]; //跳到下一个树节点
int p = j; //每次从当前树节点开始
while (p && cnt[p] != -1) {
res = res + cnt[p];
cnt[p] = 0; //去除标记
p = ne[p];
}
}
cout << res << endl;
return 0;
}
单词
输入 \(n\) 个单词,所有的单词组成一篇文章,求每个单词在文章中出现的次数
数据范围
\(1 \le n \le 200\),总长度 \(\le 10^6\)
输入样例
3
a
aa
aaa
输出样例
6
3
1
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n;
int tr[N][26], f[N], idx;
int q[N], ne[N];
char str[N];
int id[210];
void insert(int x) {
int p = 0;
for (int i = 0; str[i]; i ++ ) {
int t = str[i] - 'a';
if (!tr[p][t]) tr[p][t] = ++ idx;
p = tr[p][t];
f[p] ++ ;
}
id[x] = p; //记录每个单词的结尾所在的地方
}
void build() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i ++ )
if (tr[0][i])
q[ ++ tt] = tr[0][i];
while (hh <= tt) {
int t = q[hh ++ ];
for (int i = 0; i < 26; i ++ ) {
int &p = tr[t][i];
if (!p) p = tr[ne[t]][i];
else {
ne[p] = tr[ne[t]][i];
q[ ++ tt] = p;
}
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ ) {
cin >> str;
insert(i);
}
build();
for (int i = idx - 1; i >= 0; i -- ) f[ne[q[i]]] += f[q[i]];
for (int i = 0; i < n; i ++ ) cout << f[id[i]] << endl; //输出次数
return 0;
}
基础算法
排序
函数
sort(a.begin(), a.end()); //STL的默认排序,从小到大
sort(a.begin(), a.end(), greater<int>); //从大到小
bool cmp(int &a, int &b) { //排序函数
return a < b;
}
sort(a.begin(), a.end(), cmp);
bool operator< (const Node &W) const { //结构体重构排序(Node为结构体名)
return a < W.a;
}
快速排序
方法
每次递归把比目标值小的数放在左边,大于放在右边,等于的情况不影响排序所以无所谓左右
说明
通过传入的数组以及左右端点来进行判断,可以用来查找数组中第 \(k\) 大的数
int quick_sort(int a[], int l, int r, int k) { //查询数组中第k大的数
if (l == r) return a[l];
int mid = a[l + r >> 1], i = l - 1, j = r + 1;
while (i < j) {
while (a[ ++ i] < mid);
while (a[ -- j] > mid);
if (i < j) swap(a[i], a[j]);
}
int len = j - l + 1; //左边元素个数为j - l + 1个
if (k <= len) return quick_sort(a, l, j, k); //只需要判断k在那一边,然后递归下去即可
else return quick_sort(a, j + 1, r, k - len);
}
归并排序
方法
与快速排序类似,一个先递归后排序,一个先排序后递归。
说明
除了排序外,可以用来求逆序对的数量
LL res; // 计算逆序对的数量
int a[N], b[N]; //b为中间数组
void merge_sort(int l, int r) {
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(l, mid);
merge_sort(mid + 1, r);
int t = 0, i = l, j = mid + 1;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) b[t ++ ] = a[i ++ ];
else { //说明出现了逆序对
res += mid - i + 1;
b[t ++ ] = a[j ++ ];
}
}
while (i <= mid) b[t ++ ] = a[i ++ ];
while (j <= r) b[t ++ ] = a[j ++ ];
for (int i = l, j = 0; i <= r; i ++ , j ++ ) a[i] = b[j]; //排序结束后重新赋值
}
二分
说明
只有目标区间存在单调性才可以使用二分进行计算
时间复杂度
\(O(logn)\)
大于等于
说明
在指定区间内查询第一个大于等于目标值的结果(值/下标)
while (l < r) {
LL mid = (l + r) >> 1;
if (a[mid] >= x) r = mid; //判断条件,可以自定义
else l = mid + 1;
}//l,r都是最终结果,
小于等于
说明
在指定区间内查询最后一个小于等于目标值的结果(值/下标)
while (l < r) {
LL mid = (l + r + 1) >> 1;
if (a[mid] <= x) l = mid; //判断条件,可以自定义
else r = mid - 1;
}
浮点数
说明
方法同上,可以控制精度
while (r - l >= 1e-7) { //1e-7为精度
double mid = (l + r) / 2;
if (mid * mid * mid >= x) r = mid; //判断条件
else l = mid;
}
三分
说明
用来求取单峰值函数的极值
凸函数的极大值
整型
while (l < r) {
LL lmid = l + (r - l) / 3;
LL rmid = r - (r - l) / 3;
if (check(lmid) <= check(rmid)) l = lmid + 1; //哪一端的值小,就从对应端收缩
else r = rmid - 1;
}
cout << max(check(l), check(r)); //max取极大值
浮点型
for (int i = 0; i < 300; i ++ ) { //通过循环来保障精度
double lmin = l + (r - l) / 3;
double rmid = r - (r - l) / 3;
if (check(lmid) <= check(rmid)) l = lmid; //哪一端的值小,就从对应端收缩
else r = rmid;
}
凹函数的极小值
整型
while (l < r) {
LL lmid = l + (r - l) / 3;
LL rmid = r - (r - l) / 3;
if (check(lmid) >= check(rmid)) l = lmid + 1; //哪一端的值大,就从对应端收缩
else r = rmid - 1;
}
cout << min(check(l), check(r)); //min取极小值
浮点型
for (int i = 0; i < 300; i ++ ) { //通过循环来保障精度
double lmin = l + (r - l) / 3;
double rmid = r - (r - l) / 3;
if (check(lmid) >= check(rmid)) l = lmid; //哪一端的值大,就从对应端收缩
else r = rmid;
}
高精度
加
数据范围
\(1 \le len \le 1e5\),$0\le num $
vector<int> add(vector<int> &A, vector<int> &B) { //A和B的位数存放由低位到高位
if (A.size() < B.size()) return add(B, A);
int t = 0;
vector<int> C;
for (int i = 0; i < A.size(); i ++ ) {
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C; //位数存放由低位到高位
}
减
数据范围
\(1 \le len \le 1e5\),$0\le num $
bool cmp(vector<int> &A, vector<int> &B) { //判断A和B的大小来判断是否需要输出负数
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i -- ) { //A和B的位数存放由低位到高位,所以从后向前进行
if (A[i] != B[i]) //判断
return A[i] > B[i];
}
return true;
}
vector<int> sub(vector<int> &A, vector<int> &B) { //A和B的位数存放由低位到高位
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ ) {
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除多余的0
return C; //位数存放由低位到高位
}
if (cmp(A, B)) C = sub(A, B); //判断结果是否是负数
else cout << '-', C = sub(B, A);
乘
高精 \(\times\) 低精度
数据范围
\(1 \le len \le 1e5\),\(0\le b \le 1e9\)
vector<int> mul(vector<int> &A, LL B) { //A的位数存放由低位到高位
LL t = 0;
vector<int> C;
for (int i = 0; i < A.size() || t; i ++ ) {
if (i < A.size()) t += A[i] * B;
C.push_back(t % 10);
t = t / 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除多余的0
return C; //位数存放由低位到高位
}
高精 \(\times\) 高精
数据范围
\(1 \le len \le 2000\),\(0 \le num\)
vector<int> mul(vector<int> &A, vector<int> &B) { //A和B的位数存放由低位到高位
vector<int> C(A.size() + B.size()); //必须要开辟的范围,用于遍历
int t = 0;
for (int i = 0; i < A.size(); i ++ )
for (int j = 0; j < B.size(); j ++ )
C[i + j] += A[i] * B[j];
for (int i = 0; i < C.size() || t; i ++ ) {
t += C[i];
if (i >= C.size()) C.push_back(t % 10); //如果超过了已有位数,进行扩充
else C[i] = t % 10;
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除多余的0
return C; //位数存放由低位到高位
}
除
高精 \(\div\) 低精
数据范围
\(1 \le len \le 1e5\),\(0< b \le 1e9\)
vector<int> div(vector<int> &A, LL B, LL &r) { //A的位数存放由低位到高位, r为余数
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- ) {
r = r * 10 + A[i];
C.push_back(r / B);
r %= B;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除多余的0
return C; //位数存放由低位到高位
}
高精 \(\div\) 高精
void clear(vector<int> &C) { //去除多余的0
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
reverse(C.begin(), C.end());
}
void sub(vector<int> &r,vector<int> &B) { //r-B的返回值存储在r中
LL t = 0;
for (int i = r.size() - 1, j = B.size() - 1; i >= 0; i -- , j -- ) {
t = r[i] - t;
if (j >= 0) t -= B[j];
r[i] = (t + 10) % 10;
if (t < 0) t = 1;
else t = 0;
}
clear(r);
}
bool cmp(vector<int> &r, vector<int> &B) { //判断是否可以整除,或者说A是否大于等于B
if (r.size() > B.size()) return true;
else if (r.size() == B.size()) {
for (int i = 0; i < r.size(); i ++ )
if (r[i] != B[i])
return r[i] > B[i];
return true;
} else return false;
}
vector<int> div(vector<int> &A, vector<int> &B, vector<int> &r) { //A和B位数存放由低位到高位, r为余数,同样由低位到高位存放
vector<int> C;
reverse(B.begin(), B.end());
LL flag = 0;
for (int i = A.size() - 1; i >= 0; i -- ) {
r.push_back(A[i]);
clear(r); //去除多余的0
int j = 0;
while (cmp(r, B)) {
clear(r);
flag = 1;
j ++ ;
sub(r, B);
}
if (flag) C.push_back(j);
}
reverse(C.begin(), C.end());
reverse(r.begin(), r.end());
return C; //位数存放由低位到高位
}
前缀和
一维
说明
通过预处理,可以用 \(O(1)\) 的时间复杂度来求出一段指定区间的和
$S[i] = $ 前 \(i\) 个元素的和
s[i] = s[i - 1] + a[i]; //预处理
s[r] - s[l - 1] //求取l~r这个区间内的元素的和
二维
说明
通过预处理,可以用 \(O(1)\) 的时间复杂度来求出一段指定子矩阵的和
$S[i][j] = $ 第 \(i\) 行 \(j\) 列格子左上部分所有元素的和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; //预处理
s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] //(x1, y1)~(x2, y2)矩阵元素和
三维
说明
通过预处理,可以用 \(O(1)\) 的时间复杂度来求出一段指定子矩阵的和
s[i][j][k] = a[i][j][k] + s[i - 1][j][k] + s[i][j - 1][k] + s[i][j][k - 1] - s[i - 1][j - 1][k] - s[i - 1][j][k - 1] - s[i][j - 1][k - 1] + s[i - 1][j - 1][k - 1]; //预处理
s[x2][y2][z2] - s[x1 - 1][y2][z2] - s[x2][y1 - 1][z2] - s[x2][y2][z1 - 1] + s[x1 - 1][y1 - 1][z2] + s[x1 - 1][y2][z1 - 1] + s[x2][y1 - 1][z1 - 1] - s[x1 - 1][y1 - 1][z1 - 1]; //(x1, y1, z1)~(x2, y2, z2)矩阵元素的和
差分
前缀和的一种扩展用法,在原本求和的基础上增加了区间修改这一操作。
例:将$l \(~\) r$中每个数字都增加 \(c\)
一维
//l为左端点,r为右端点,计算后进行一次前缀和计算为原数组,再进行一次为前缀和数组
a[l] += x; //更新左端点
a[r+1] -= x; //更新右端点
a[i] += a[i-1]; //前缀和
二维
void input(int x1,int y1,int x2,int y2,int c) { //区间增加
a[x1][y1] += c;
a[x1][y2+1] -= c;
a[x2+1][y1] -= c;
a[x2+1][y2+1] += c;
}
a[i][j] = a[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]; //前缀和
离散化
说明
可能原数组的数据范围很大,但数的个数较小,可以通过离散化处理后再进行计算。
vector<int> idx; //存储需要离散化的元素
sort(idx.begin(), idx.end()); //将所有元素排序
idx.erase(unique(idx.begin(), idx.end()), idx.end()); //去掉重复的元素
int find(int x) { //STL方法
return lower_bound(idx.begin(), idx.end(), x) - idx.begin(); //返回值为对应数值的下标
}
int find(int x) { //二分
int l = 0, r = idx.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (idx[mid] >= x) r = mid;
else l = mid + 1;
}
return l;
}
搜索与图论
DFS(深度优先遍历)
说明:通过递归的方式来搜索每种情况,需要注意退出以及剪枝的条件,容易出现栈溢出,死循环等情况,注意遍历完当前情况后需要恢复现场。
\(n\)−皇后问题是指将 \(n\) 个皇后放在 \(n×n\) 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
输入格式
共一行,包含整数 \(n\)。
输出格式
每个解决方案占 \(n\) 行,每行输出一个长度为 \(n\) 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
数据范围
\(1 \le n \le 9\)
输入样例
4
输出样例
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int n;
char g[N][N]; //存储棋盘
bool col[N], dg[N * 2], udg[N * 2]; //col列,dg对角线,udg反对角线
void dfs(int u) {
if (u == n) { //说明遍历到终点
for (int i = 0; i < n; i ++ ) cout << g[i] << endl;
cout << endl;
return;
}
for (int i = 0; i < n; i ++ ) {
if (!col[i] && !dg[u + i] && !udg[n - u + i]) { //当前位置可以进行改变
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1); //深度增加
col[i] = dg[u + i] = udg[n - u + i] = false; //还原现场
g[u][i] = '.';
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ ) { //初始化
for (int j = 0; j < n; j ++ ) {
g[i][j] = '.';
}
}
dfs(0);
return 0;
}
BFS(广度优先遍历)
说明:每次更新节点都由当前的队头元素进行,可以保证遍历到新的节点时,所使用的变化次数最少
给定一个 \(n×m\) 的二维整数数组,用来表示一个迷宫,数组中只包含 \(0\) 或 \(1\),其中 \(0\) 表示可以走的路,\(1\) 表示不可通过的墙壁。
输入格式
第一行包含两个整数 \(n\) 和 \(m\)
接下来 \(n\) 行,每行包含 \(m\) 个整数(\(0\) 或 \(1\)),表示完整的二维数组迷宫
输出格式
输出一个整数,表示从 \((1,1)\) 移动至\((n, m)\)的最少移动次数。
数据范围
\(1 \le n,m \le 100\)
输入样例
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例
8
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n, m;
int g[N][N], d[N][N]; //g存储数值,d存储遍历到当前节点的最小步数
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}; //四向搜索,上右下左
int bfs() {
queue<PII> q;
memset(d, -1, sizeof d);
d[0][0] = 0;
q.push({0, 0});
while (q.size()) {
auto t = q.front();
q.pop();
for (int i = 0; i < 4; i ++ ) { //遍历下一步可以向哪走
int x = t.first + dx[i], y = t.second + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue; //超出范围
if (d[x][y] != -1 || g[x][y] == 1) continue; //说明已经被遍历过了,或者撞墙了
d[x][y] = d[t.first][t.second] + 1; //步数加1
q.push({x, y});
}
}
return d[n - 1][m - 1];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < m; j ++ ) {
cin >> g[i][j];
}
}
cout << bfs() << endl;
return 0;
}
树与图的深度优先遍历
给定一颗树,树中包含 \(n\) 个结点(编号 \(1∼n\))和 \(n−1\) 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点
被称为树的重心。
输入格式
第一行包含整数 \(n\) ,表示树的结点数。接下来 \(n−1\) 行,每行包含两个整数 \(a\) 和 \(b\),表示点 \(a\) 和点 \(b\) 之间存在一条边。
输出格式
输出一个整数 \(m\) ,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
\(1 \le n \le 10^5\)
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例
4
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = N * 2; //由于是无向图,所以建两倍的边
int n;
int ans = N;
int h[N], e[M], ne[M], idx; //邻接表
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs(int u, int fa) { //返回以u为根节点的子树中节点的个数,包括u
int size = 0, sum = 0; //记录最大的子树节点个数,以及所有节点个数的和
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
int s = dfs(j, u);
size = max(size, s); //所有子树点树的最大值
sum += s;
}
size = max(size, n - sum - 1); //上半部分的点的个数
ans = min(ans, size);
return sum + 1; //加上u点本身
}
int main() {
memset(h, -1, sizeof h); //邻接表初始化
cin >> n;
for (int i = 1; i < n; i ++ ) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
dfs(1, -1); //随便从一个节点开始
cout << ans << endl;
return 0;
}
树与图的广度优先遍历
说明:通过BFS暴力查找最短路,将距离队头元素距离为1的未遍历过的节点都加到队列中,可以保证路径长度最短
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 \(1\),点的编号为 \(1∼n\)。
请你求出 \(1\) 号点到 \(n\) 号点的最短距离,如果从 \(1\) 号点无法走到 \(n\) 号点,输出 \(−1\)。
输入格式
第一行包含两个整数 \(n\) 和 \(m\)。
接下来 \(m\) 行,每行包含两个整数 \(a\) 和 \(b\),表示存在一条从 \(a\) 走到 \(b\) 的长度为 \(1\) 的边。
输出格式
输出一个整数,表示 \(1\) 号点到 \(n\) 号点的最短距离。
数据范围
$ 1 \le n,m \le 10^5$
输入样例
4 5
1 2
2 3
3 4
1 3
1 4
输出样例
1
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int h[N], e[N], ne[N], idx;
int dist[N]; //点i到1的距离
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int bfs() {
memset(dist, -1, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
while (q.size()) {
auto t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] == -1) { //说明还没被遍历过
dist[j] = dist[t] + 1;
q.push(j);
}
}
}
return dist[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
add(a, b); //单向边
}
cout << bfs() << endl;
return 0;
}
拓扑排序
说明
当一个节点的入度为 \(0\) 那么该节点就可以添加进队列,当所有节点都进队时,便形成了一种拓扑排序
时间复杂度:\(O(n + m)\) \(n\) 表示点数,\(m\) 表示边数
int d[N]; //表示第i个节点的入度
vecotr<int> q; //存储拓扑序列
bool topsort() {
q.clear();
for (int i = 1; i <= n; i ++ ) {
if (!d[i])
q.push_back(i); //入度为0入队
}
for (int hh = 0; hh < q.size(); hh ++ ) {
int t = q[hh]; //取出队头元素
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
d[j] -- ;
if (!d[j]) q.push_back(j); //说明入度为0可以入队
}
}
return q.size() == n; //节点个数和n相同
}
朴素版Dijkstra
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 \(1\) 号点到 \(n\) 号点的最短距离,如果无法从 \(1\) 号点走到 \(n\) 号点,则输出 \(−1\)。
时间复杂度
\(O(n^2 + m)\) \(n\) 表示点数,\(m\)表示边数
数据范围
\(1 \le n \le 500\),\(1 \le m \le 10^5\)
输入样例
3 3
1 2 2
2 3 1
1 3 4
输出样例
3
说明
每次用最小的未搜索过的,距离源点最近的点来更新其余节点,可以保证 \(dist\) 距离最小
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m;
int g[N][N]; //g[a][b]表示a到b的长度
int dist[N]; //点i到源点的距离
bool st[N]; //表示当前节点的最小距离已经确定了
int dijkstra() { //求1号点到n号点的最短路,不存在返回-1
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ ) {
int t = -1; //在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
for (int j = 1; j <= n; j ++ ) //用t更新其他点的距离
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main() {
cin >> n >> m;
memset(g, 0x3f, sizeof g);
while (m -- ) {
int a, b, c;
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
cout << dijkstra() << endl;
return 0;
}
堆优化版Dijkstra
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 \(1\) 号点到 \(n\) 号点的最短距离,如果无法从 \(1\) 号点走到 \(n\) 号点,则输出 \(−1\)。
时间复杂度
\(O(mlogn)\),\(n\) 表示点数,\(m\) 表示边数
数据范围
\(1 \le n,m \le 1.5*10^5\)
输入样例
3 3
1 2 2
2 3 1
1 3 4
输出样例
3
说明
通过优先队列来更新最短距离,相比朴素版效率更高
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; //小根堆,每次取出的堆顶元素最小
heap.push({0, 1});
while (heap.size()) {
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue; //首次出堆元素最小,后续无法保证
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[ver] + w[i]) { //最短路,当前可以被更新
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j}); //更新后的值插入堆中
}
}
}
if (dist[n] == INF) return -1;
return dist[n];
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
while (m -- ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
bellman-ford
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 \(1\) 号点到 \(n\) 号点的最多经过 \(k\) 条边的最短距离,如果无法从 \(1\) 号点走到 \(n\) 号点,输出 impossible。
注意
图中可能 存在负权回路 。
时间复杂度
\(O(nm)\),\(n\) 表示点数,\(m\) 表示边数
数据范围
\(1≤n,k≤500\),\(1≤m≤10000\)
输入样例
3 3 1
1 2 1
2 3 1
1 3 3
输出样例
3
说明
分为 \(k\) 步进行操作,每步都进行进行一次松弛操作,\(dist[n]\) 表示从源点到 \(n\) 走 \(k\) 步的最短路径
当步数大于 \(n\) 且更新了节点说明存在负环
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 10010;
struct Edge { //存储所有的边
int a, b, c;
}edges[M];
int n, m, k;
int dist[N];
int last[N];
void bellman_ford() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i ++ ) { //当步数多于n次且更新了节点,说明存在负环
memcpy(last, dist, sizeof dist); //dist拷贝至last
for (int j = 0; j < m; j ++ ) {
auto &c = edges[j]; //引用,懒得打名字用
dist[c.b] = min(dist[c.b], last[c.a] + c.c); //a的dist可能被更新过了,所以用last来跟新
}
}
}
int main() {
cin >> n >> m >> k;
for (int i = 0; i < m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
edges[i] = {a, b, c}; //从a到b连一条边,边长为c
}
bellman_ford();
if (dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl; //只有从根节点出发的路径才能满足条件
else cout << dist[n] << endl;
return 0;
}
spfa
最短路
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 \(1\) 号点到 \(n\) 号点的最短距离,如果无法从 \(1\) 号点走到 \(n\) 号点,则输出 impossible。
数据保证不存在负权回路。
时间复杂度
平均情况\(O(m)\) ,最坏 \(O(nm)\),n为点数,m为边数
数据范围
\(1 \le n, m \le 10^5\)
输入样例
3 3
1 2 5
2 3 -3
1 3 4
输出样例
2
说明
本质是队列优化Bellman-ford算法,与dijkstra不同的是,spfa无法保证出队时最小,只有遍历完后才能确定
无负权边的情况下建议写dijkstra,spfa容易被卡
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
bool st[N]; //判断是否在队列中
int dist[N]; //存储距离
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1); //从1开始存进队列
st[1] = true;
while (q.size()) {
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
if (!st[j]) { //保证元素不会反复入队
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m -- ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
int t = spfa();
if (t == 0x3f3f3f3f) cout << "impossible" << endl;
else cout << t << endl;
return 0;
}
判负环
给定一个 \(n\) 个点 \(m\) 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你判断图中是否存在负权回路。
时间复杂度
\(O(nm)\),\(n\)表示点数,\(m\) 表示边数
数据范围
\(1\le n \le 2000\),\(1 \le m \le 10000\)
输入样例
3 3
1 2 -1
2 3 4
3 1 -4
输出样例
Yes
说明
一共有 \(n\) 条边,\(cnt[x]\) 表示 \(1\) 到 \(x\) 的最短路所花费的步数,当步数大于等于 \(n\) 时,图中存在负环
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2010, M = 10010;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int dist[N], cnt[N]; //存储最短距离,以及花费的步数
bool st[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa() {
queue<int> q;
for (int i = 1; i <= n; i ++ ) { //全部入队是因为假设了一个长度为0的虚拟源点
st[i] = true;
q.push(i);
}
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; //n个点,n-1条边,超过说明存在负环
if (!st[j]) {
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m -- ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
if (spfa()) cout << "Yes" << endl; //有负环
else cout << "No" << endl;
return 0;
}
Floyd
最短路
说明
可以求取任意一个节点到另外一个节点的最短路
时间复杂度
\(O(n^3)\)
数据范围
\(1 \le n \le 200\)
void init() { //边在初始化后用邻接矩阵存储
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= n; j ++ ) {
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
}
}
}
void floyd() { //dist[x][y] >= INF/2说明不存在边
for (int k = 1; k <= n; k ++ ) {
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= n; j ++ ) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
传递闭包
给定 \(n\) 个变量和 \(m\) 个不等式。其中 \(n\) 小于等于 \(26\),变量分别用前 \(n\) 的大写英文字母表示。
不,即若 \(A>B\) 且 \(B>C\),则 \(A>C\)。
请从前往后遍历每对关系,每次遍历时判断:
- 如果能够确定全部关系且无矛盾,则结束循环,输出确定的次序;
- 如果发生矛盾,则结束循环,输出有矛盾;
- 如果循环结束时没有发生上述两种情况,则输出无定解。
输入格式
第一行包含两个整数 \(n\) 和 \(m\)。
接下来 \(m\) 行,每行包含一个不等式,不等式全部为小于关系。
输出格式
结果可能为下列三种之一:
- 如果可以确定两两之间的关系,则输出
"Sorted sequence determined after t relations: yyy...y.",其中't'指迭代次数,'yyy...y'是指升序排列的所有变量。 - 如果有矛盾,则输出:
"Inconsistency found after t relations.",其中't'指迭代次数。 - 如果没有矛盾,且不能确定两两之间的关系,则输出
"Sorted sequence cannot be determined."。
数据范围
\(2 \le n\le26\) ,变量为大写字母\(A\) ~ \(Z\)
输入样例
4 6
A<B
A<C
B<C
C<D
B<D
A<B
3 2
A<B
B<A
26 1
A<Z
0 0
输出样例
Sorted sequence determined after 4 relations: ABCD.
Inconsistency found after 2 relations.
Sorted sequence cannot be determined.
说明:传递闭包的时间复杂度是\(O(mn^3)\),慎写!
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 26;
int n, m;
bool g[N][N], d[N][N]; //g用来存储两点的关系,d是判断传递闭包后是否存在冲突
bool st[N]; //st用来存储那些值被使用过
void floyd() {
memcpy(d, g, sizeof d);
for (int k = 0; k < n; k ++ ) {
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < n; j ++ ) {
d[i][j] |= d[i][k] && d[k][j]; //i<k且k<j时i<j传递闭包
}
}
}
}
int check() {
for (int i = 0; i < n; i ++ ) {
if (d[i][i]) //自己小于自己,一定出现冲突,反之不存在冲突
return 2;
}
for (int i = 0; i < n; i ++ ) {
for (int j = 0; j < i; j ++ ) {
if (!d[i][j] && !d[j][i]) //存在两个点之间没有关系,说明当前情况无解
return 0;
}
}
return 1;
}
char get_min() {
for (int i = 0; i < n; i ++ ) {
if (!st[i]) { //未使用过
bool flag = true;
for (int j = 0; j < n; j ++ ) { //未使用的字母没有比它大的便满足条件
if (st[j]) continue;
if (d[j][i]) { //j比i小的情况存在,判断失败
flag = false;
break;
}
}
if (flag) {
st[i] = true;
return i + 'A';
}
}
}
}
int main() {
cin >> n >> m;
int type = 0, t;
memset(g, 0, sizeof g);
memset(st, 0, sizeof st);
for (int i = 1; i <= m; i ++ ) {
char c[5];
cin >> c;
int a = c[0] - 'A', b = c[2] - 'A';
if (!type) { //有解或者无解后都不需要继续判断
g[a][b] = true; //说明a小于b
floyd(); //每一轮都需要重新判断
type = check(); //判断是否可以继续计算
if (type) t = i;
}
}
if (!type) cout << "Sorted sequence cannot be determined." << endl; //没有出现冲突
else if (type == 2) printf("Inconsistency found after %d relations.\n", t); //表示从第几次开始出现矛盾
else {
printf("Sorted sequence determined after %d relations: ", t);
for (int i = 0; i < n; i ++ ) cout << get_min(); //取出当前未使用过的最小值
cout << "." << endl;
}
}
Prim
时间复杂度
\(O(n^2 + m)\),\(n\) 表示点数,\(m\) 表示边数
数据范围
\(1\le n \le 500\), \(1 \le m \le 10^5\)
说明
最小生成树,表示形成这颗树的花费最小,每次找到距离最小生成树最小的边,将这条边加入树中,保证结果最小
int n; //n表示点数
int g[N][N]; //邻接矩阵,存储所有边
int dist[N]; //存储其他点到当前最小生成树的距离
bool st[N]; //存储每个点是否已经在生成树中
int prim() {
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ ) { //一共你n-1条边,第0次选择一个点可以在循环中更新关系
int t = -1;
for (int j = 1; j <= n; j ++ ) {
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
if (i && dist[t] == INF) return INF; //说明当前的图形成不了树
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal
时间复杂度
\(O(mlogm)\),\(n\) 表示点数,\(m\) 表示边数
数据范围
\(1 \le n \le 10^5\),\(1 \le m \le 2 * 10^5\)
说明
通过并查集来辅助计算,每次取出未遍历过的最小的边,判断这条边是否可以加入最小生成树中,可以的话便合并这个边的两个端点所在的集合,一共有 \(n - 1\) 条边需要加入
int n, m; //n是点数,m是边数
int p[N]; //并查集
struct Edge {
int a, b, w;
bool operator< (const Edge &W) const {
return w < W.w;
}
}edges[M];
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int kruskal() {
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; //并查集初始化
int res = 0, cnt = 0; //最小生成树的花费,当前合并了多少个数;
for (int i = 0; i < m; i ++ ) {
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) {
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF; //合并的点的数量小于最小生成树的条件
return res;
}
染色法判定二分图
给定一个 \(n\) 个点 \(m\) 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 \(n\) 和 \(m\)。
接下来 \(m\) 行,每行包含两个整数 \(u\) 和 \(v\),表示点 \(u\) 和点 \(v\) 之间存在一条边。
输出格式
如果是二分图输出Yes,否者输出No
数据范围
\(1 \le n,m \le 10^5\)
输入样例
4 4
1 3
1 4
2 3
2 4
输出样例
Yes
时间复杂度
\(O(nm)\),\(n\) 表示点数,\(m\) 表示边数
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int color[N]; //用来存储每个点的颜色
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool dfs(int u, int c) { //将u染色成c
color[u] = c;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!color[j]) {
if (!dfs(j, 3 - c)) return false; //染相反的颜色
} else if (color[j] == c) return false; //被遍历过了,且颜色冲突
}
return true;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
bool flag = true;
for (int i = 1; i <= n; i ++ ) {
if (!color[i]) {
if (!dfs(i, 1)) { //递归染色,当前节点如果没被遍历过便不会有颜色,所以无论染那种颜色都无所谓
flag = false;
break;
}
}
}
if (flag) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
匈牙利算法
给定一个二分图,其中左半部包含 \(n_1\) 个点(编号 \(1∼n_1\)),右半部包含 \(n_2\) 个点(编号 \(1∼n_2\)),二分图共包含 \(m\) 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 \(G\),在 \(G\) 的一个子图 \(M\) 中,\(M\) 的边集 \({E}\) 中的任意两条边都不依附于同一个顶点,则称 \(M\) 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 \(n_1\)、 \(n_2\) 和 \(m\)。
接下来 \(m\) 行,每行包含两个整数 \(u\) 和 \(v\),表示左半部点集中的点 \(u\) 和右半部点集中的点 \(v\) 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
\(1≤n1,n2≤500\)
\(1≤u≤n_1\)
\(1≤v≤n_2\)
\(1≤m≤10^5\)
输入样例
2 2 4
1 1
1 2
2 1
2 2
输出样例
2
时间复杂度
\(O(nm)\),\(n\) 表示点数,\(m\) 表示边数
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m; //n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; //邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; //存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; //表示第二个集合中的每个点是否已经被遍历过
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool find(int x) {
for (int i = h[x]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) { //目标点未被遍历过
st[j] = true;
if (match[j] == 0 || find(match[j])) { //当前值没有匹配,或者能为目标原本的匹配对象找到新匹配值
match[j] = x;
return true;
}
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
add(a, b);
}
int res = 0;
for (int i = 1; i <= n1; i ++ ) {
memset(st, false, sizeof st); //每次初始化后需要重新判断
if (find(i)) res ++ ; //如果当前能匹配到值,那么计数增加
}
cout << res << endl;
return 0;
}
Flood Fill
农夫约翰有一片 \(N∗M\) 的矩形土地。
最近,由于降雨的原因,部分土地被水淹没了。
现在用一个字符矩阵来表示他的土地。
每个单元格内,如果包含雨水,则用“\(W\)”表示,如果不含雨水,则用”\(.\)”表示。
现在,约翰想知道他的土地中形成了多少片池塘。
每组相连的积水单元格集合可以看作是一片池塘。
每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。
请你输出共有多少片池塘,即矩阵中共有多少片相连的“\(W\)”块。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
接下来 \(N\) 行,每行包含 \(M\) 个字符,字符为“\(W\)”或“\(.\)”,用以表示矩形土地的积水状况,字符之间没有空格。
输出格式
输出一个整数,表示池塘的数目
输入样例
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
输出样例
3
数据范围
\(1 \le N,M \le1000\)
时间复杂度
\(O(nm)\)
说明
遍历所有的节点,当前节点没有被标记说明它是一个新的池塘的节点,把与这个节点所在的池塘中的节点全部标记即可。
参考代码
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 1010;
int n, m;
char g[N][N]; //存储图形
bool st[N][N]; //判断当前节点是否被遍历过
int res;
void bfs(int sx, int sy) {
queue<PII> q;
st[sx][sy] = true;
q.push({sx, sy});
while (q.size()) {
PII t = q.front();
q.pop();
for (int i = t.x - 1; i <= t.x + 1; i ++ ) //遍历以t为中心点的九宫格
for (int j = t.y - 1; j <= t.y + 1; j ++ ) {
if (i < 0 || i >= n || j < 0 || j >= m) continue;
if (st[i][j] || g[i][j] == '.') continue;
st[i][j] = true;
q.push({i, j}); //继续搜索下一轮
}
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> g[i];
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (!st[i][j] && g[i][j] == 'W') { //当前节点未被遍历过,计数增加
bfs(i, j);
res ++ ;
}
cout << res << endl;
return 0;
}
多源BFS
给定一个 \(N\) 行 \(M\) 列的 \(01\) 矩阵 \(A\),\(A[i][j]\) 与 \(A[k][l]\) 之间的曼哈顿距离定义为:
\(dist(i,j,k,l)=|i−k|+|j−l|\)
输出一个 \(N\) 行 \(M\) 列的整数矩阵 \(B\),其中:
\(B[i][j]=min_{1≤x≤N,1≤y≤M,A[x][y]=1}dist(i,j,x,y)\)
输入格式
第一行两个整数 \(N,M\)
接下来一个 \(N\) 行 \(M\) 列的 \(01\) 矩阵,数字之间没有空格
输出格式
一个 \(N\) 行 \(M\) 列的矩阵 \(B\),相邻两个整数之间用一个空格隔开。
数据范围
\(1 \le N,M \le 1000\)
输入样例
3 4
0001
0011
0110
输出样例
3 2 1 0
2 1 0 0
1 0 0 1
说明
找到所有节点到最近的 \(1\) 的曼哈顿距离,可以反向思考,从1所在的节点走到任意节点的最少步数
参考代码
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 1010;
int n, m;
char g[N][N];
int dist[N][N]; //B数组,存储距离
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1}; //四向搜索
void bfs() {
memset(dist, -1, sizeof dist);
queue<PII> q;
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ ) {
if (g[i][j] == '1') {
dist[i][j] = 0;
q.push({i, j});
}
}
}
while (q.size()) {
auto t = q.front(); //可以保证出队元素的距离最小,同时保证由这个点到达的其余节点的距离最小
q.pop();
for (int i = 0; i < 4; i ++ ) {
int a = t.x + dx[i], b = t.y + dy[i];
if (a < 1 || a > n || b < 1 || b > m) continue;
if (dist[a][b] != -1) continue;
dist[a][b] = dist[t.x][t.y] + 1; //距离增加
q.push({a, b});
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) scanf("%s", g[i] + 1); //保证数组下标
bfs();
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ ) cout << dist[i][j] << ' ';
cout << endl;
}
return 0;
}
最小步数模型
Rubik 先生在发明了风靡全球的魔方之后,又发明了它的二维版本——魔板。
这是一张有 \(8\) 个大小相同的格子的魔板:
1 2 3 4
8 7 6 5
我们知道魔板的每一个方格都有一种颜色。
这 \(8\) 种颜色用前 \(8\) 个正整数来表示。
可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,沿顺时针方向依次取出整数,构成一个颜色序列。
对于上图的魔板状态,我们用序列 \((1,2,3,4,5,6,7,8)\) 来表示,这是基本状态。
这里提供三种基本操作,分别用大写字母 A,B,C 来表示(可以通过这些操作改变魔板的状态):
A:交换上下两行;
B:将最右边的一列插入到最左边;
C:魔板中央对的4个数作顺时针旋转。
对于每种可能的状态,这三种基本操作都可以使用。
你要编程计算用最少的基本操作完成基本状态到特殊状态的转换,输出基本操作序列。
注意
数据保证一定有解。
输入格式
输出文件的第一行包括一个整数,表示最短操作序列的长度。
如果操作序列的长度大于0,则在第二行输出字典序最小的操作序列。
输出格式
输入数据中的所有数字均为 \(1\) 到 \(8\) 之间的整数。
输入样例
2 6 8 4 5 7 3 1
输出样例
7
BCABCCB
说明
通过BFS暴力搜索,同时判断当前搜索的状态是否存在即可
参考代码
#include <bits/stdc++.h>
using namespace std;
unordered_map<string, int> st; //判断当前状态是否出现过
queue<pair<string, string>> q;
int main() {
string res(8, '0');
for (int i = 0; i < 8; i ++ ) cin >> res[i];
q.push({"12345678", ""}); //初始化
st["12345678"] = 1;
while (q.size()) {
auto t = q.front();
q.pop();
string s = t.first; //当前的魔版状态
string now = t.second; //当前使用的操作
if (s == res) {
if (now == "") cout << 0 << endl;
else cout << now.size() << endl << now << endl;
break;
}
string A, B, C;
A = {s[7], s[6], s[5], s[4], s[3], s[2], s[1], s[0]}; //三种变换操作
B = {s[3], s[0], s[1], s[2], s[5], s[6], s[7], s[4]};
C = {s[0], s[6], s[1], s[3], s[4], s[2], s[5], s[7]};
if (!st[A]) st[A] = 1, q.push({A, now + "A"});
if (!st[B]) st[B] = 1, q.push({B, now + "B"});
if (!st[C]) st[C] = 1, q.push({C, now + "C"});
}
return 0;
}
双端队列广搜
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。
翰翰的家里有一辆飞行车。
有一天飞行车的电路板突然出现了故障,导致无法启动。
电路板的整体结构是一个 \(R\) 行 \(C\) 列的网格(\(R,C≤500\)),如下图所示。
每个格点都是电线的接点,每个格子都包含一个电子元件。
电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。
在旋转之后,它就可以连接另一条对角线的两个接点。
电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。
她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。
不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。
注意
只能走斜向的线段,水平和竖直线段不能走。
输入格式
第一行包含正整数 \(R\) 和 \(C\),表示电路板的行数和列数。
之后 \(R\) 行,每行 \(C\) 个字符,字符是"/"和"\"中的一个,表示标准件的方向。
输出格式
对于每组测试数据,在单独的一行输出一个正整数,表示所需的最小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。
输入样例
1
3 5
\\/\\
\\///
/\\\\
输出样例
1
数据范围
\(1 \le R,C \le500\)
说明
需要交换的代价是 \(1\),不交换代价是 \(0\) ,代价 \(0\) 放在队首,代价 \(1\) 放在队尾,可以保证\(bfs\)的准确性

红色坐标代表对应的点坐标,蓝色坐标表示跨越字符的格子坐标
双端队列的写法很适合这种边权为 \(01\) 的图
参考代码
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 510, M = N * N;
int n, m;
char g[N][N];
int dist[N][N];
bool st[N][N];
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1}; //dx、dy是坐标点(宽搜路线)的偏移
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1}; //ix、iy是每当按坐标点走过一步时, 所能跨越字符所在格子的位置
char cs[] = "\\/\\/"; //跨越时的对应图形需求
int bfs() {
memset(dist, 0x3f, sizeof dist); //最短路同款
memset(st, 0, sizeof st); //未搜索过
dist[0][0] = 0; //起始点
deque<PII> q;
q.push_back({0, 0});
while (q.size()) {
PII t = q.front();
q.pop_front();
if (st[t.x][t.y]) continue;
st[t.x][t.y] = true;
for (int i = 0; i < 4; i ++ ) {
int a = t.x + dx[i], b = t.y + dy[i]; //点坐标偏移
if (a < 0 || b < 0 || a > n || b > m) continue;
int ca = t.x + ix[i], cb = t.y + iy[i]; //判断代价的坐标
int d = dist[t.x][t.y] + (g[ca][cb] != cs[i]);
if (d < dist[a][b]) {
dist[a][b] = d;
if (g[ca][cb] != cs[i]) q.push_back({a, b}); //放在队尾
else q.push_front({a, b}); //放在队头
}
}
}
return dist[n][m];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> g[i];
int t = bfs();
if (t == 0x3f3f3f3f) puts("NO SOLUTION");
else cout << t << endl;
return 0;
}
双向广搜
已知有两个字串 \(A\), \(B\) 及一组字串变换的规则(至多 \(6\) 个规则):
\(A1→B1\)
\(A2→B2\)
…
规则的含义为:在 \(A\) 中的子串 \(A1\) 可以变换为 \(B1\)、\(A2\) 可以变换为 \(B2…\)。
例如:\(A\)=abcd \(B\)=xyz
变换规则为:
abc\(→\) xu,ud \(→\) y,y \(→\) yz
则此时,\(A\) 可以经过一系列的变换变为 \(B\),其变换的过程为:
abcd \(→\) xud \(→\) xy \(→\) xyz
共进行了三次变换,使得 \(A\) 变换为 \(B\)。
注意,一次变换只能变换一个子串,例如 \(A\)=aa \(B\)=bb
变换规则为:
a \(→\) b
此时,不能将两个 a 在一步中全部转换为 b,而应当分两步完成。
输入格式
输入格式如下:
\(A\) \(B\)
\(A_1\) \(B_1\)
\(A_2\) \(B_2\)
… …
第一行是两个给定的字符串 \(A\) 和 \(B\)。
接下来若干行,每行描述一组字串变换的规则。
所有字符串长度的上限为 \(20\)。
输出格式
若在 \(10\) 步(包含 \(10\) 步)以内能将 \(A\) 变换为 \(B\) ,则输出最少的变换步数;否则输出 NO ANSWER!。
输入样例
abcd xyz
abc xu
ud y
y yz
输出样例
3
说明
假设每次决策数量时 \(K\) 那么直接 BFS,最坏情况空间是 \(K^{10}\) 用双向 BFS 可以优化成 \(2K^{5}\)
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 6;
int n;
string A, B;
string a[N], b[N]; //变换规则
//一次需要扩展一层,不然会出现问题
int extend(queue<string> &q, unordered_map<string, int> &da, unordered_map<string, int> &db, string a[], string b[]) { //当前队列,以扩展的,可以匹配的,扩展规则
int d = da[q.front()]; //扩展所有距离为d的点
while (q.size() && da[q.front()] == d) {
auto t = q.front();
q.pop();
for (int i = 0; i < n; i ++ )
for (int j = 0; j < t.size(); j ++ )
if (t.substr(j, a[i].size()) == a[i]) { //进行匹配
string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size()); //拼凑出新的字符串
if (db.count(r)) return da[t] + db[r] + 1;
if (da.count(r)) continue;
da[r] = da[t] + 1;
q.push(r);
}
}
return 11;
}
int bfs() {
if (A == B) return 0;
queue<string> qa, qb; //两个方向的搜索,方法和bfs相同
unordered_map<string, int> da, db; //存储变化到当前状态的最小步数
qa.push(A), qb.push(B);
da[A] = db[B] = 0;
int step = 0; //判断扩展次数是否大于10
while (qa.size() && qb.size()) {
int t;
if (qa.size() < qb.size()) t = extend(qa, da, db, a, b); //a中个数比b小,扩展a更优
else t = extend(qb, db, da, b, a); //反向匹配
if (t <= 10) return t;
if ( ++ step == 10) return -1;
}
return -1;
}
int main() {
cin >> A >> B;
while (cin >> a[n] >> b[n]) n ++ ;
int t = bfs();
if (t == -1) cout << "NO ANSWER!" << endl;
else cout << t << endl;
}
A*
给定一张 \(N\) 个点(编号 \(1,2…N\)),\(M\) 条边的有向图,求从起点 \(S\) 到终点 \(T\) 的第 \(K\) 短路的长度,路径允许重复经过点或边。
注意: 每条最短路中至少要包含一条边。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
接下来 \(M\) 行,每行包含三个整数 \(A,B\) 和 \(L\),表示点 \(A\) 与点 \(B\) 之间存在有向边,且边长为 \(L\)。
最后一行包含三个整数 \(S,T\) 和 \(K\),分别表示起点 \(S\),终点 \(T\) 和第 \(K\) 短路。
输出格式
输出占一行,包含一个整数,表示第 \(K\) 短路的长度,如果第 \(K\) 短路不存在,则输出 \(−1\)。
输入样例
2 2
1 2 5
2 1 4
1 2 2
输出样例
14
说明
- 第\(K\)短路,就是终点出队\(K\)次的距离。注意:当起点和终点一样时,K++
- 只要从\(S\)能到达\(T\),就一定存在第\(K\)短路,故不存在则一定不能从\(S\)到达\(T\)
- 估价函数:从该点到终点的最短距离,即求一遍\(Dijkstra\),大于等于\(0\),小于等于真实值
- 取出堆顶,记录出队次数,把该点能枚举到的所有点都放入小根堆
参考代码
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef pair<int, PII> PIII;
const int N = 1010, M = 200010;
int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
void add(int h[], int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra() {
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, T}); //终点
memset(dist, 0x3f, sizeof dist);
dist[T] = 0;
while (heap.size()) {
auto t = heap.top();
heap.pop();
int ver = t.y;
if (st[ver]) continue;
st[ver] = true;
for (int i = rh[ver]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[ver] + w[i]) {
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
}
int astar() {
priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
heap.push({dist[S], {0, S}}); // 谁的d[u]+f[u]更小 谁先出队列
while (heap.size()) {
auto t = heap.top();
heap.pop();
int ver = t.y.y, distance = t.y.x;
cnt[ver] ++ ; //如果终点已经被访问过k次了 则此时的ver就是终点T 返回答案
if (cnt[T] == K) return distance;
for (int i = h[ver]; ~i; i = ne[i]) {
int j = e[i];
/*
如果走到一个中间点都cnt[j]>=K,则说明j已经出队k次了,且astar()并没有return distance,
说明从j出发找不到第k短路(让终点出队k次),
即继续让j入队的话依然无解,
那么就没必要让j继续入队了
*/
if (cnt[j] < K)
heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
// 按真实值+估计值 = d[j]+f[j] = dist[S->t] + w[t->j] + dist[j->T] 堆排
// 真实值 dist[S->t] = distance+w[i]
}
}
// 终点没有被访问k次
return -1;
}
int main() {
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
for (int i = 0; i < m; i ++ ) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h, a, b, c);
add(rh, b, a, c);
}
scanf("%d%d%d", &S, &T, &K);
if (S == T) K ++ ; // 起点==终点时 则d[S→S] = 0 这种情况就要舍去 ,总共第K大变为总共第K+1大
// 从各点到终点的最短路距离 作为估计函数f[u]
dijkstra();
printf("%d\n", astar());
return 0;
}
DFS之连通性模型
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 \(W\) 和 \(H\),分别表示 \(x\) 方向和 \(y\) 方向瓷砖的数量。
在接下来的 \(H\) 行中,每行包括 \(W\) 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
输入样例
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例
45
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 25;
int n, m;
char g[N][N];
bool st[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dfs(int x, int y) {
int cnt = 1;
st[x][y] = true;
for (int i = 0; i < 4; i ++ ) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m) continue; //边界处理
if (g[a][b] != '.') continue;
if (st[a][b]) continue;
cnt += dfs(a, b);
}
return cnt;
}
int main() {
while (cin >> m >> n, n || m) {
for (int i = 0; i < n; i ++ ) cin >> g[i];
int x, y;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
if (g[i][j] == '@') {
x = i;
y = j;
}
memset(st, 0, sizeof st);
cout << dfs(x, y) << endl;
}
return 0;
}
DFS之搜索顺序
给定 \(n\) 个正整数,将它们分组,使得每组中任意两个数互质。
至少要分成多少个组?
输入格式
第一行是一个正整数 \(n\)。
第二行是 \(n\) 个不大于10000的正整数。
输出格式
一个正整数,即最少需要的组数。
输入样例
6
14 20 33 117 143 175
输出样例
3
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
int n;
int p[N];
int group[N][N]; //分组
bool st[N];
int ans = N;
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
bool check(int group[], int gc, int i) {
for (int j = 0; j < gc; j ++ )
if (gcd(p[group[j]], p[i]) > 1)
return false;
return true;
}
//当前要放在哪个分组;要放在该分组的第几个位置;从哪个位置开始选择元素【组合套路(定一个遍历顺序)】;当前已分组完毕的元素个数
void dfs(int g, int gc, int tc, int start) {
if (g >= ans) return; //剪枝 + 防止死循环
if (tc == n) ans = g;
bool flag = true; //从start开始找,是否有元素不能放到gr组中
for (int i = start; i < n; i ++ )
if (!st[i] && check(group[g], gc, i)) {
st[i] = true;
group[g][gc] = i;
dfs(g, gc + 1, tc + 1, i + 1);
st[i] = false;
flag = false;
}
//新开一个分组
//由于dfs每层之间确定了顺序,所以期间是会有元素被漏掉的,【比如一开始你找的一串序列(1)是1,2,3,4 但是第二次(2)是1,3,4 很显然此时
//(2)还有一个3没有得到分组,需要从start=0开始再把它找出来! 因此这样做仿佛有点浪费时间呢!!】
//因此当所有元素都不能放进当前分组的时候 或者 当start=n-1了但是元素没有全部分组完毕时,要重新从start=0开始找,并且一定要有st数组!!!不然会把一个元素重复的分组!
if (flag) dfs(g + 1, 0, tc, 0);
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> p[i];
dfs(1, 0, 0, 0);
cout << ans << endl;
return 0;
}
DFS之剪枝与优化
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 \(50\) 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 \(64\) 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
输入样例
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
输出样例
6
5
说明
- length | sum
- 优先搜索顺序:从大到小枚举
- 排除等效冗余:
- 按照组合数方式枚举。
- 如果当前木棍加到当前棒中失败了,则直接略过后面所有长度相等的木棍
- 如果是木棒的第一根木棍失败了,则一定失败
- 如果是木棒的最后一根木棍失败了,则一定失败
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 70;
int n;
int w[N];
int sum, length;
bool st[N];
bool dfs(int u, int cur, int start) {
if (u * length == sum) return true;
if (cur == length) return dfs(u + 1, 0, 0);
for (int i = start; i < n; i ++ ) { //剪枝3-1
if (st[i] || cur + w[i] > length) continue;
st[i] = true;
if (dfs(u, cur + w[i], i + 1)) return true;
st[i] = false;
if (!cur || cur + w[i] == length) return false; //剪枝3-3&3-4
int j = i;
while (j < n && w[j] == w[i]) j ++ ; //剪枝3-2
i = j - 1;
}
return false;
}
int main() {
while (cin >> n, n) {
memset(st, 0, sizeof st);
sum = 0;
for (int i = 0; i < n; i ++ ) {
cin >> w[i];
sum += w[i];
}
sort(w, w + n); //剪枝2
reverse(w, w + n);
length = 1;
while (true) {
if (sum % length == 0 && dfs(0, 0, 0)) { //剪枝1
cout << length << endl;
break;
}
length ++ ;
}
}
return 0;
}
迭代加深
满足如下条件的序列 \(X\)(序列中元素被标号为 \(1、2、3…m\))被称为“加成序列”:
- \(X[1]=1\)
- \(X[m]=n\)
- \(X[1]<X[2]<…<X[m−1]<X[m]\)
- 对于每个 \(k\)(\(2≤k≤m\))都存在两个整数 \(i\) 和 \(j\) (\(1≤i,j≤k−1\),\(i\) 和 \(j\) 可相等),使得 \(X[k]=X[i]+X[j]\)。
你的任务是:给定一个整数 \(n\),找出符合上述条件的长度 \(m\) 最小的“加成序列”。
如果有多个满足要求的答案,只需要找出任意一个可行解。
输入格式
输入包含多组测试用例。
每组测试用例占据一行,包含一个整数 \(n\)。
当输入为单行的 \(0\) 时,表示输入结束。
输出格式
对于每个测试用例,输出一个满足需求的整数序列,数字之间用空格隔开。
每个输出占一行。
输入样例
5
7
12
15
77
0
输出样例
1 2 4 5
1 2 4 6 7
1 2 4 8 12
1 2 4 5 10 15
1 2 4 8 9 17 34 68 77
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
int path[N];
bool dfs(int u, int k) { // u表示当前层数, k表示最大的层数
if (u == k) return path[u - 1] == n;
bool st[N] = {0}; // 通过 bool数组排除等效冗余
for (int i = u - 1; i >= 0; i -- )
for (int j = i; j >= 0; j -- ) {
int s = path[i] + path[j];
if (s > n || s <= path[u - 1] || st[s]) continue; // path一定是递增的
st[s] = true;
path[u] = s;
if (dfs(u + 1, k)) return true;
}
return false;
}
int main() {
path[0] = 1;
while (cin >> n, n) {
int k = 1;
while (!dfs(1, k)) k ++ ; // 不断扩大范围
for (int i = 0; i < k; i ++ ) cout << path[i] << ' ';
cout << endl;
}
return 0;
}
双向DFS
达达帮翰翰给女生送礼物,翰翰一共准备了 \(N\) 个礼物,其中第 \(i\) 个礼物的重量是 \(G[i]\)。
达达的力气很大,他一次可以搬动重量之和不超过 \(W\) 的任意多个物品。
达达希望一次搬掉尽量重的一些物品,请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。
输入格式
第一行两个整数,分别代表 \(W\) 和 \(N\)。
以后 \(N\) 行,每行一个正整数表示 \(G[i]\)。
输出格式
仅一个整数,表示达达在他的力气范围内一次性能搬动的最大重量。
输入样例
20 5
7
5
4
18
1
输出样例
19
参考代码
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1 << 24;
int n, m, k;
int g[50], weights[N]; // 存储所有物品的重量,weights存储能凑出来的所有的重量
int cnt = 0;
int ans; // 用ans来记录一个全局最大值
// u表示当前枚举到哪个数了, s表示当前的和
void dfs(int u, int s) {
if (u == k) { // 如果我们当前已经枚举完第k个数(下标从0开始的)了, 就把当前的s, 加到weights中去
weights[cnt ++ ] = s;
return;
}
if ((LL)s + g[u] <= m) dfs(u + 1, s + g[u]); // 选这个物品, 做一个可行性剪枝
dfs(u + 1, s); // 枚举当前不选这个物品
}
void dfs2(int u, int s) {
if (u == n) { // 如果已经找完了n个节点, 那么需要二分一下
int l = 0, r = cnt - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (weights[mid] + (LL)s <= m) l = mid;
else r = mid - 1;
}
if (weights[l] + (LL)s <= m) ans = max(ans, weights[l] + s);
return;
}
if ((LL)s + g[u] <= m) dfs2(u + 1, s + g[u]); // 选择当前这个物品
dfs2(u + 1, s); // 不选择当前这个物品
}
int main() {
cin >> m >> n;
for (int i = 0; i < n; i ++ ) cin >> g[i];
sort(g, g + n); // 优化搜索顺序(从大到小)
reverse(g, g + n);
k = n / 2; // 防止 n = 1时,出现死循环
dfs(0, 0); // 把前k个物品的重量打一个表
sort(weights, weights + cnt); // 做完之后, 把weights数组从小到大排序
int t = 1; // 判重
for (int i = 1; i < cnt; i ++ )
if (weights[i] != weights[i - 1])
weights[t ++ ] = weights[i];
cnt = t;
// 从k开始, 当前的和是0
dfs2(k, 0);
cout << ans << endl;
return 0;
}
IDA*
给定 \(n\) 本书,编号为 \(1∼n\)。
在初始状态下,书是任意排列的。
在每一次操作中,可以抽取其中连续的一段,再把这段插入到其他某个位置。
我们的目标状态是把书按照 \(1∼n\) 的顺序依次排列。
求最少需要多少次操作。
输入格式
第一行包含整数 \(T\),表示共有 \(T\) 组测试数据。
每组数据包含两行,第一行为整数 \(n\),表示书的数量。
第二行为 \(n\) 个整数,表示 \(1∼n\) 的一种任意排列。
同行数之间用空格隔开。
输出格式
每组数据输出一个最少操作次数。
如果最少操作次数大于或等于 \(5\) 次,则输出 5 or more。
每个结果占一行。
输入样例
3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10
输出样例
2
3
5 or more
说明
估价函数设计:假设有\(cnt\)个位置使得相邻的位置并不是相差\(1\) (即这两个数不能捆在一起处理),而每次移动会改变\(3\)个数后面的数,所以操作数量为\(\lceil\frac{cnt}{3}\rceil=\lfloor\frac{cnt + 2}{3}\rfloor\)
\(IDA*\)是用\(IDDFS\)实现的(迭代加深)
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int n;
int q[N]; // 书的编号
int w[5][N]; // 恢复现场使用
int f() { // 估价函数
int cnt = 0;
for (int i = 0; i + 1 < n; i ++ )
if (q[i + 1] != q[i] + 1)
cnt ++ ;
return (cnt + 2) / 3;
}
bool check() { // 检查序列是否已经有序
for (int i = 0; i + 1 < n; i ++ )
if (q[i + 1] != q[i] + 1)
return false;
return true;
}
bool dfs(int depth, int max_depth) { // k: 当前迭代深度; depth: 迭代加深最大深度
if (depth + f() > max_depth) return false;
if (check()) return true;
for (int len = 1; len <= n; len ++ ) // 先遍历长度
for (int l = 0; l + len - 1 < n; l ++ ) { // 再遍历左端点
int r = l + len - 1;
for (int k = r + 1; k < n; k ++ ) {
memcpy(w[depth], q, sizeof q);
int x, y;
for (x = r + 1, y = l; x <= k; x ++, y ++ ) q[y] = w[depth][x];
for (x = l; x <= r; x ++, y ++ ) q[y] = w[depth][x];
if (dfs(depth + 1, max_depth)) return true;
memcpy(q, w[depth], sizeof q);
}
}
return false;
}
int main() {
int T;
cin >> T;
while (T -- ) {
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> q[i];
int depth = 0;
while (depth < 5 && !dfs(0, depth)) depth ++ ;
if (depth >= 5) puts("5 or more");
else cout << depth << endl;
}
return 0;
}
差分约束
差分约束算法
- 找最少,求上界,用最长路,\(b >= a + c\),\(add(a, b, c);\)
- 找最多,求下界,用最短路,\(b <= a + c\),\(add(a, b,c);\)
幼儿园里有 \(N\) 个小朋友,老师现在想要给这些小朋友们分配糖果,要求每个小朋友都要分到糖果。
但是小朋友们也有嫉妒心,总是会提出一些要求,比如小明不希望小红分到的糖果比他的多,于是在分配糖果的时候, 老师需要满足小朋友们的 \(K\) 个要求。
幼儿园的糖果总是有限的,老师想知道他至少需要准备多少个糖果,才能使得每个小朋友都能够分到糖果,并且满足小朋友们所有的要求。
输入格式
输入的第一行是两个整数 \(N,K\)。
接下来 \(K\)行,表示分配糖果时需要满足的关系,每行 \(3\) 个数字 \(X,A,B\)。
- 如果 \(X=1\).表示第 \(A\) 个小朋友分到的糖果必须和第 \(B\) 个小朋友分到的糖果一样多。
- 如果 \(X=2\),表示第 \(A\) 个小朋友分到的糖果必须少于第 \(B\) 个小朋友分到的糖果。
- 如果 \(X=3\),表示第 \(A\) 个小朋友分到的糖果必须不少于第 \(B\) 个小朋友分到的糖果。
- 如果 \(X=4\),表示第 \(A\) 个小朋友分到的糖果必须多于第 \(B\) 个小朋友分到的糖果。
- 如果 \(X=5\),表示第 \(A\) 个小朋友分到的糖果必须不多于第 \(B\) 个小朋友分到的糖果。
小朋友编号从 \(1\) 到 \(N\)。
输出格式
输出一行,表示老师至少需要准备的糖果数,如果不能满足小朋友们的所有要求,就输出 \(−1\)。
输入样例
5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1
输出样例
11
说明
每个人获得的糖果的下届便是超级源点到每个点的距离,考虑求至少用多少糖果,那么可以用最长路进行计算。
参考代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, M = 300010;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
LL dist[N];
int q[N], cnt[N]; //统计到当前点总共有多少条边了
bool st[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
bool spfa() {
int hh = 0, tt = 1;
memset(dist, -0x3f, sizeof dist); //最长路 dist[j] < dist[t] + w[i] 初始化为-INF
dist[0] = 0;
q[0] = 0;
st[0] = true;
while (hh != tt) {
int t = q[ -- tt] ;
st[t] = false; //不在栈中 状态 = false
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (dist[j] < dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n + 1) return false; //有负环 无解
if (!st[j]) {
q[tt ++ ] = j;
st[j] = true;
}
}
}
}
return true;
}
int main() {
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- ) {
int x, a, b;
scanf("%d%d%d", &x, &a, &b);
if (x == 1) add(b, a, 0), add(a, b, 0); // A = B
else if (x == 2) add(a, b, 1); //B >= A + 1
else if (x == 3) add(b, a, 0); // A >= B
else if (x == 4) add(b, a, 1); // A >= B + 1
else add(a, b, 0); //B >= A
}
//每个同学都要分到糖果 x[i] >= 1
//超级源点0 x[i] >= x[0]+1 <=> x[i] >= 1
for (int i = 1; i <= n; i ++ ) add(0, i, 1);
if (!spfa()) puts("-1");
else {
LL res = 0;
for (int i = 1; i <= n; i ++ ) res += dist[i];
printf("%lld\n", res);
}
return 0;
}
最近公共祖先
倍增求LCA
给定一棵包含 \(n\) 个节点的有根无向树,节点编号互不相同,但不一定是 \(1∼n\)。
有 \(m\) 个询问,每个询问给出了一对节点的编号 \(x\) 和 \(y\),询问 \(x\) 与 \(y\) 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 \(n\) 行每行一对整数 \(a\) 和 \(b\),表示 \(a\) 和 \(b\) 之间有一条无向边。如果 \(b\) 是 \(-1\),那么 \(a\) 就是树的根;
第 \(n+2\) 行是一个整数 \(m\) 表示询问个数;
接下来 \(m\) 行,每行两个不同的正整数 \(x\) 和 \(y\),表示一个询问。
输出格式
对于每一个询问,若 \(x\) 是 \(y\) 的祖先则输出 \(1\),若 \(y\) 是 \(x\) 的祖先则输出 \(2\),否则输出 \(0\)。
输入样例
10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19
输出样例
1
0
0
0
2
说明
设 $$F[x, k]$$ 表示 $$x$$ 的 $$2^k$$ 级祖先,$$F[x, k] = F[F[x, k-1]][k-1]$$
- 设 $$d[x]$$ 表示 $$x$$ 的深度。不妨设 $$d[x] \geq d[y]$$
- 用二进制拆分思想,把 $$x$$ 向上调到与 $$y$$ 同一深度
- 若此时 $$x = y$$,则说明已经找到 LCA,LCA 就是 $$x$$;否则 $$x$$、$$y$$ 一起继续往上跳,直到相遇
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 4e4 + 10, M = N * 2;
int n;
int depth[N], fa[N][16]; //往上跳2^k步后的父亲节点
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void bfs(int root) { //宽搜不容易因为递归层数过多爆栈
memset(depth, 0x3f, sizeof depth);
// 哨兵depth[0] = 0: 如果从i开始跳2^j步会跳过根节点
// fa[fa[j][k-1]][k-1] = 0
// 那么fa[i][j] = 0 depth[fa[i][j]] = depth[0] = 0
depth[0] = 0, depth[root] = 1;
queue<int> q;
q.push(root);
while (q.size()) {
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j] > depth[t] + 1) { //说明j还没被搜索过
depth[j] = depth[t] + 1;
q.push(j); //把第depth[j]层的j加进队列
fa[j][0] = t; //j往上跳2^0步后就是t
for (int k = 1; k <= 15; k ++ ) { //fa[j][k] = fa[fa[j][k - 1]][k - 1];
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b); // 为方便处理 当a在b上面时 把a b 互换
for (int k = 15; k >= 0; k -- ) { //把深度更深的a往上跳到b
if (depth[fa[a][k]] >= depth[b]) { //从大到小保证不会跳错
a = fa[a][k];
}
}
if (a == b) return a; //如果跳到了说明答案就是a
for (int k = 15; k >= 0; k -- ) { //同时向上跳,保证跳到祖先节点的下面
if (fa[a][k] != fa[b][k]) {
a = fa[a][k];
b = fa[b][k];
}
}
return fa[a][0]; //父节点就是最近公共祖先
}
int main() {
cin >> n;
memset(h, -1, sizeof h);
int root;
while (n -- ) {
int a, b;
cin >> a >> b;
if (b == -1) root = a;
else add(a, b), add(b, a);
}
bfs(root); // 初始化fa[i][j]
cin >> n;
while (n -- ) {
int a, b;
cin >> a >> b;
int p = lca(a, b);
if (p == a) puts("1");
else if (p == b) puts("2");
else puts("0");
}
return 0;
}
tarjan求LCA
给出 \(n\) 个点的一棵树,多次询问两点之间的最短距离。
注意:
- 边是无向的。
- 所有节点的编号是 \(1,2,…,n\)。
输入格式
第一行为两个整数 \(n\) 和 \(m\)。\(n\) 表示点数,\(m\) 表示询问次数;
下来 \(n−1\) 行,每行三个整数 \(x,y,k\),表示点 \(x\) 和点 \(y\) 之间存在一条边长度为 \(k\);
再接下来 \(m\) 行,每行两个整数 \(x,y\),表示询问点 \(x\) 到点 \(y\) 的最短距离。
树中结点编号从 \(1\) 到 \(n\)。
输出格式
共 \(m\) 行,对于每次询问,输出一行询问结果。
输入样例
3 2
1 2 10
3 1 15
1 2
3 2
输出样例
10
25
说明
在深度优先遍历的任意时刻,树中节点分为三类:
- 已经访问完毕并且回溯的节点,标记为 \(2\)
- 已经开始递归,但尚未回溯的节点。这些节点就是当前正在访问的节点 \(x\) 以及 \(x\) 的祖先。标记为 \(1\)
- 没有访问的节点。没有标记
考虑使用 并查集 优化,当一个节点被标记为 \(2\) 时,合并到它的父节点(合并时它的父节点标记一定为 \(1\),且单独构成一个集合)
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e4 + 10, M = 2 * N;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int p[N], dist[N]; //每个点和1号点的距离
int st[N];
int res[M];
vector<PII> q[M]; //把询问存下来
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dist[j] = dist[u] + w[i];
dfs(j, u);
}
}
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
void tarjan(int u) {
st[u] = 1; //当前路径点标记为1
// u这条路上的根节点的左下的点用并查集合并到根节点
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) {
tarjan(j); //往左下搜
p[j] = u; //从左下回溯后把左下的点合并到根节点
}
}
// 对于当前点u 搜索所有和u
for (auto item : q[u]) {
int y = item.first, id = item.second;
if (st[y] == 2) { //如果查询的这个点已经是左下的点(已经搜索过且回溯过,标记为2)
int anc = find(y); //y的根节点
// x到y的距离 = d[x]+d[y] - 2*d[lca]
res[id] = dist[u] + dist[y] - dist[anc] * 2; //第idx次查询的结果 res[idx]
}
}
//点u已经搜索完且要回溯了 就把st[u]标记为2
st[u] = 2;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
for (int i = 0; i < m; i ++ ) {
int a, b;
cin >> a >> b;
if (a != b) {
q[a].push_back({b, i});
q[b].push_back({a, i});
}
}
for (int i = 1; i <= n; i ++ ) p[i] = i;
dfs(1, -1);
tarjan(1);
for (int i = 0; i < m; i ++ ) {
cout << res[i] << endl;
}
return 0;
}
次小生成树
给定一张 \(N\) 个点 \(M\) 条边的无向图,求无向图的严格次小生成树。
设最小生成树的边权之和为 \(sum\),严格次小生成树就是指边权之和大于 \(sum\) 的生成树中最小的一个。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
接下来 \(M\) 行,每行包含三个整数 \(x, y, z\),表示点 \(x\) 和点 \(y\) 之间存在一条边,边的权值为 \(z\)。
输出格式
包含一行,仅一个整数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
输入样例
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
输出样例
11
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = 3e5 + 10, INF = 0x3f3f3f3f;
struct Edge {
int a, b, w;
bool used;
bool operator< (const Edge& t) const {
return w < t.w;
}
}edge[M];
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int depth[N], fa[N][17], d1[N][17], d2[N][17];
int p[N];
// d1[i][j] : 从i这个节点开始向上跳2^j步, 这条路径上的最小边权
// d2 次小边权
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
LL kruskal() {
LL res = 0;
for (int i = 1; i <= n; i ++ ) p[i] = i;
sort(edge, edge + m);
for (int i = 0; i < m; i ++ ) {
int a = find(edge[i].a), b = find(edge[i].b), w = edge[i].w;
if (a != b) {
edge[i].used = true;
p[a] = b;
res += w;
}
}
return res;
}
// 建树,建造出最小生成树
void build() {
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ ) {
if (edge[i].used) {
int a = edge[i].a, b = edge[i].b, w = edge[i].w;
add(a, b, w);
add(b, a, w);
}
}
}
// 用最近公共祖先来求所有路径离根节点的最大的一条边,和次大的一条边
void bfs() {
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[1] = 1;
queue<int> q;
q.push(1);
while (q.size()) {
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j] > depth[t] + 1) {
q.push(j); // 宽度优先
fa[j][0] = t; // 更新一下 fa(i, 0);
depth[j] = depth[t] + 1; // bfs更新层次
d1[j][0] = w[i];
d2[j][0] = -INF; // 更新一下d1, d2
// 只有一条边不存在次长路
// 都已经更新到这个点了, 之前路径上的距离也都算出来了
// 所以都可以更新出d1, d2 fa,
for (int k = 1; k <= 16; k ++ ) { // 开始跳
int anc = fa[j][k - 1]; // 这anc是跳一半的位置
fa[j][k] = fa[anc][k - 1]; // 求得跳2^k之后的位置
// distance存储的是j开始跳一半的数据
// d1[j][k - 1] 跳一般的最大边
// d2[j][k - 1] 跳一半的次大边
// d1[anc][k - 1] 跳另一半的最大边
// d2[anc][k - 1] 跳另一半的次大边
int distance[4] = {d1[j][k - 1], d2[j][k - 1], d1[anc][k - 1], d2[anc][k - 1]};
d1[j][k] = d2[j][k] = -INF; // 整条路径的最大值和次大值先初始化为-INF
for (int u = 0; u < 4; u ++ ) {
int d = distance[u];
if (d > d1[j][k]) { // 更新一下最大值和次大值
d2[j][k] = d1[j][k];
d1[j][k] = d;
} else if(d!= d1[j][k] && d > d2[j][k]) {
d2[j][k] = d;
}
}
}
}
}
}
}
// a -> b w是一条非树边
int lca(int a, int b, int w) {
vector<int> q;
if (depth[a] < depth[b]) swap(a, b);
for (int k = 16; k >= 0; k -- ) { // 向上跳, 跳到同层
if (depth[fa[a][k]] >= depth[b]) {
q.push_back(d1[a][k]); // 每跳一次,记录一下这路径上的最大值
q.push_back(d2[a][k]); // 次大值
a = fa[a][k];
}
}
// 跳到同一层,但是不是同一个节点的话,就继续跳
if (a != b) {
for (int k = 16; k >= 0; k -- ) {
if (fa[a][k] != fa[b][k]) { // 把这所有东西都存下来
q.push_back(d1[a][k]);
q.push_back(d2[a][k]);
q.push_back(d1[b][k]);
q.push_back(d2[b][k]);
a = fa[a][k];
b = fa[b][k];
}
}
// 已经找到公共祖先了,公共祖先就是 fa[a][0] = fa[b][0] = anc
// 把这边也存下来
q.push_back(d1[a][0]);
q.push_back(d2[a][0]);
q.push_back(d1[b][0]);
q.push_back(d2[b][0]);
}
// 找到公共祖先的
int dist1 = -INF, dist2 = -INF;
for (int i = 0; i < q.size(); i ++ )
{
int d = q[i];
// 这里规定dist1 一定严格大于 dist2 (dist2是严格次小值)
if (d > dist1) dist2 = dist1, dist1 = d;
// 如果这里 d = dist 而且 d = dist2, 令dist2 = d的话,就会有 dist1 = dist2
else if (d != dist1 && d > dist2) dist2 = d;
}
if (w > dist1) return w - dist1; // 看一下这个非树边是否大于dist1, 是的话就替换
// 返回变大了多少
// w 一定是 >= dist1 > dist2
// 如果第一个if不满足, 那一定有 w = dist1
if (w > dist2) return w - dist2; // 看一下这个非树边是否大于dist2, 是的话就替换
// 返回变大了多少
return INF;
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
edge[i] = {a, b, c};
}
LL sum = kruskal();
build();
bfs();
LL res = 1e18;
for (int i = 0; i < m; i ++ ) {
if (!edge[i].used) { // 枚举一下所有非树边
int a = edge[i].a, b = edge[i].b, w = edge[i].w;
res = min(res, sum + lca(a, b, w)); // 看看替换后的结果, 取最小值
}
}
cout << res << endl;
return 0;
}
有向图的强连通分量
强连通图:一张有向图 \(G\),若对于图中任意两个节点 \(x, y\),既存在从 \(x\) 到 \(y\) 的路径,也存在从 \(y\) 到 \(x\) 的路径,则称该图是强连通图。
有向图的极大连通子图被称为 强联通分量,记为 SCC。
tarjan算法计算“割韧值”:
当节点 \(x\) 第一次被访问时,把 \(x\) 入栈中,初始化 \(low[x]=dfn[x]\)
扫描 \(x\) 的出边 \((x, y)\)
(1) 若 \(y\) 没被访问过,则说明 \((x, y)\) 是树枝边,递归访问 \(y\),从 \(y\) 回溯之后,令 \(low[u]=\min(low[x], low[y])\)
(2) 若 \(y\) 被访问过且 \(y\) 在栈中,则令 \(low[u]=\min(low[x], dfn[y])\)
若 \(u\) 回溯到根,判断是否有 \(low[x]=dfn[x]\),若有则不断从栈中淡出结点,直到 \(x\) 出栈
强联通分量判定法则:在追溯值的计算过程中,若从 \(x\) 回溯前,有 \(low[x]=dfn[x]\) 成立,则将由 \(x\) 到其他所有节点构成一个强联通分量
每一头牛的愿望就是变成一头最受欢迎的牛。
现在有 \(N\) 头牛,编号从 \(1\) 到 \(N\),给你 \(M\) 对整数 \((A,B)\),表示牛 \(A\) 认为牛 \(B\) 受欢迎。
这种关系是具有传递性的,如果 \(A\) 认为 \(B\) 受欢迎,\(B\) 认为 \(C\) 受欢迎,那么牛 \(A\) 也认为牛 \(C\) 受欢迎。
你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
输入格式
第一行两个数 \(N,M\);
接下来 \(M\) 行,每行两个数 \(A,B\),意思是 \(A\) 认为 \(B\) 是受欢迎的(给出的信息有可能重复,即有可能出现多个 \(A,B\))。
输出格式
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
输入样例
3 3
1 2
2 1
2 3
输出样例
1
说明
这题图中强连通分量中点之间一定可以相互到达所以强连通分量我们可以看成一个点
对强连通分量进行缩点然后建立边这样我们就可以得到一个拓扑图了
可以发现如果出度为0的点有两个以上那么没有答案
拓扑图必定有一个出度为0的点如果只有一个出度为0的点那么这个强连通分量里的元素个数就是需要的答案
所以再求强连通分量的时候要注意开一个数组维护一下强连通分量中元素的个数
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 50010;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, Size[N];
int dout[N]; // 记录每个连通分量的出度
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u) {
// 当前点的时间戳
dfn[u] = low[u] = ++ timestamp;
stk[ ++ top] = u, in_stk[u] = true; // 加入栈中
//遍历u点的所有邻点
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!dfn[j]) { //如果没有遍历过
tarjan(j); // 遍历它
low[u] = min(low[u], low[j]);
}
// 当前点在栈当中
else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u]) {
++ scc_cnt; // 更新强连通分量的编号
int y;
do {
y = stk[top -- ]; //不断取出栈内元素
in_stk[y] = false;
id[y] = scc_cnt; // y元素所属的连通块编号
Size[scc_cnt] ++ ; // 该连通块内包含的点数
} while (y != u); // 直到y不等于u
}
}
int main() {
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- ) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
for (int i = 1; i <= n; i ++ )
if (!dfn[i])
tarjan(i);
// 建有向无环图
// 统计在新图中所有点的出度
for (int i = 1; i <= n; i ++ )
for (int j = h[i]; ~j; j = ne[j]) {
int k = e[j];
int a = id[i], b = id[k]; // a表示i所在连通分量的编号,b表示k所在连通分量的编号
// 如果点i和点k不在同一个连通块
// dout存的是出度,因为本题只需要出度
// 在其他题目中,可能是要建边,因为这里是构造有向无环图
if (a != b) dout[a] ++ ; // 从a走到b,a的出度++
}
// 和本题有关的部分:
// zeros是统计在新图中,出度为0的点的个数
// sum表示满足条件的点(最受欢迎的奶牛)的个数
int zeros = 0, sum = 0;
for (int i = 1; i <= scc_cnt; i ++ )
if (!dout[i]) {
zeros ++ ;
sum += Size[i];
if (zeros > 1) {
sum = 0;
break;
}
}
printf("%d\n", sum);
return 0;
}
无向图的双连通分量
边的双连通分量 (\(e-dcc\)):极大的不包含桥的连通块
点的双连通分量 (\(v-dcc\)):极大的不包含割点的连通块
割点:给定一张无向连通图 \(G\),若对于 \(x \in V\),从图中删去节点 \(x\) 以及所有与 \(x\) 关联的边后,\(G\) 分裂成两个或两个以上不相连的子图,则称 \(x\) 为 \(G\) 的割点。
桥:给定一张无向连通图 \(G\),若对于 \(e \in E\),从图中删去边 \(e\) 之后,\(G\) 分裂成两个不相连的子图,则称 \(e\) 为 \(G\) 的桥或割边。
割边判定法则:无向边 \((x, y)\) 是桥,当且仅当搜索树中存在 \(x\) 的一个子节点 \(y\),满足 \(dfn[x] < low[y]\)。
割点判定法则:若 \(x\) 不是搜索树的父节点,则 \(x\) 是割点当且仅当搜索树上存在 \(x\) 的一个子节点 \(y\),满足 \(dfn[x] \leq low[y]\)。
为了从 \(F\) 个草场中的一个走到另一个,奶牛们有时不得不路过一些她们讨厌的可怕的树。
奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径。
给出所有 \(R\) 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量,路径由若干道路首尾相连而成。
两条路径相互分离,是指两条路径没有一条重合的道路。
但是,两条分离的路径上可以有一些相同的草场。
可能有不止一条道路直接连接同一对草场,尽管如此,你仍可以在它们之间再建一条道路,作为另一条不同的道路。
输入格式
第 \(1\) 行输入 \(F\) 和 \(R\)。
接下来 \(R\) 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
输出格式
输出一个整数,表示最少的需要新建的道路数。
输入样例
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
输出样例
2
说明
给定一个连通的无向图让你进行加边操作,要求每一对点之间都至少有两条相互分离的路径,求最小的加边数。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5010, M = 2e4 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
stack<int> stk;
int dfn[N], low[N], timestamp;
int id[N], dcc_cnt;
bool is_bridge[M];
int d[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u, int from) { //from记录的是当前节点由哪条边过来的(防止反向遍历)
dfn[u] = low[u] = ++ timestamp;
stk.push(u);
for (int i = h[u]; ~i; i = ne[i]) { //先将图的所有节点的low和dnt都预处理出来
int j = e[i];
if (!dfn[j]) {
tarjan(j, i);
low[u] = min(low[u], low[j]);
//表示j节点永远都走不到u节点(u,j这两个点只能从u走到j),所以边u-j(w[i])是一条桥边
if (dfn[u] < low[j]) {
is_bridge[i] = is_bridge[i ^ 1] = true; //反向边同样是桥边
//因为一对正向边和反向边的编号都是成对出现,所以直接^1即可
// 这里i==idx 如果idx==奇数 则反向边=idx+1 = idx^1
// 如果idx==偶数 则反向边=idx-1 = idx^1
}
} else if (i != (from ^ 1)) { //from ^ 1是边from的反向边,防止再遍历回去
low[u] = min(low[u], dfn[j]); //j节点有可能是之前遍历过的点
}
}
//预处理完之后判断哪个节点的low[u] = dnt[u],说明是双联通分量的最高点
if (dfn[u] == low[u]) {
++ dcc_cnt;
int y;
do {
y = stk.top();
stk.pop();
id[y] = dcc_cnt;
} while (y != u);
}
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
tarjan(1, -1);
//遍历所有边,如果边i是桥边,在其所连的出边的点j所在双连通分量的度+1
for (int i = 0; i < idx; i ++ ) { //包含正向边和反向边,所以度为1的节点一定是叶子节点
if (is_bridge[i]) {
d[id[e[i]]] ++ ;
}
}
int cnt = 0;
//枚举所有双连通分量,需要加的边数就是:(度为1的节点个数 + 1 ) / 2
for (int i = 1; i <= dcc_cnt; i ++ ) {
if (d[i] == 1) {
cnt ++ ;
}
}
cout << (cnt + 1) / 2;
return 0;
}
给定一个由 \(n\) 个点 \(m\) 条边构成的无向图,请你求出该图删除一个点之后,连通块最多有多少。
输入格式
输入包含多组数据。
每组数据第一行包含两个整数 \(n,m\)。
接下来 \(m\) 行,每行包含两个整数 \(a,b\),表示 \(a,b\) 两点之间有边连接。
数据保证无重边。
点的编号从 \(0\) 到 \(n−1\)。
读入以一行 \(0 0\) 结束。
输出格式
每组数据输出一个结果,占一行,表示连通块的最大数量。
输入样例
3 3
0 1
0 2
2 1
4 2
0 1
2 3
3 1
1 0
0 0
输出样例
1
2
2
说明
\(dnt\) 数组可以当判重数组进行使用,用 \(tarjan\) 算法可以把每一个连通块求出来。
对于每一个连通块,如果 \(dfs[n] \leq low[j]\) 的话,删除 \(n\) 点,肯定会使得 \(j\) 所在的连通块部分成为一个新的连通块。
所以记录一下有多少个 \(j\),特别一下如果是 \(n\) 是该连通块的根节点,就会多一个连通块。
所以总的来说就是求割点,如果没有割点那答案就是连通块的个数,否则,就是删去割点后连通块的个数。
注意要特判根节点
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 3e4 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp; // dfn 和 low 数组用于存储 Tarjan 算法的时间戳和 low 值,times 用于记录时间戳
int ans, root; // ans 表示答案,root 表示 Tarjan 算法中的根节点
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u) { // Tarjan 算法求割点
dfn[u] = low[u] = ++ timestamp; // 更新时间戳和 low 值
int cnt = 0; // cnt 用于记录当前节点的儿子节点数
for (int i = h[u]; ~i; i = ne[i]) { // 遍历当前节点的所有出边
int j = e[i];
if (!dfn[j]) { // 如果目标节点还未被访问过
tarjan(j); // 递归访问目标节点
low[u] = min(low[u], low[j]); // 更新当前节点的 low 值
if (dfn[u] <= low[j]) { // 如果目标节点的 low 值大于等于当前节点的 dfn 值,则说明目标节点无法返回当前节点的父节点,即当前节点是割点
cnt ++ ;
}
} else { // 如果目标节点已经被访问过,则更新当前节点的 low 值
low[u] = min(low[u], dfn[j]);
}
}
if (root != u && cnt) cnt ++ ; // 如果当前节点不是 根节点,则将当前节点计入其父节点的儿子节点数中
ans = max(ans, cnt); // 更新答案
}
int main() {
while (cin >> n >> m, n || m) { // 处理多组输入
memset(dfn, 0, sizeof dfn); // 初始化时间戳为 0
memset(h, -1, sizeof h); // 初始化邻接表为空
idx = timestamp = 0; // 初始化边的数量和时间戳为 0
while (m -- ) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
int cnt = 0; // cnt 用于记录连通分量个数
ans = 0; // 初始化答案为 0
for (root = 0; root < n; root ++ ) { // 枚举每个节点作为 Tarjan 算法的根节点运行算法
if (!dfn[root]) { // 如果当前节点还未被访问过
cnt ++ ; // 连通分量个数加一
tarjan(root); // 运行 Tarjan 算法求割点
}
}
cout << cnt + ans - 1 << endl; // 输出答案
}
return 0;
}
欧拉回路和欧拉路径
欧拉路径
给定一张无向图,若存在一条从节点 \(S\) 到节点 \(T\) 的路径,恰好不重复不漏的经过每一条边一次,则称该路径为欧拉路。
欧拉回路
若存在一条从节点 \(S\) 出发,恰好不重复不漏地经过每条边一次,最终回到 \(S\),则称该回路为欧拉回路。
欧拉图的判定
一张无向图为欧拉图,当且仅当无向图连通,并且每个点的度数都是偶数。
给定一张图,请你找出欧拉回路,即在图中找一个环使得每条边都在环上出现恰好一次。
输入格式
第一行包含一个整数 \(t\),\(t \in \{1, 2\}\),如果 \(t = 1\),表示所给图为无向图,如果 \(t = 2\),表示所给图为有向图。
第二行包含两个整数 \(n, m\),表示图的结点数和边数。
接下来 \(m\) 行中,第 \(i\) 行两个整数 \(v_i, u_i\),表示第 \(i\) 条边(从 1 开始编号)。
- 如果 \(t = 1\) 则表示 \(v_i\) 到 \(u_i\) 有一条无向边。
- 如果 \(t = 2\) 则表示 \(v_i\) 到 \(u_i\) 有一条有向边。
图中可能有重边也可能有自环。
点的编号为从 1 到 \(n\)。
输出格式
如果无法一笔画出欧拉回路,则输出一行:NO。
否则,输出一行:YES,接下来一行输出任意一组合法方案即可。
- 如果 \(t = 1\),输出 \(m\) 个整数 \(p_1, p_2, \dots, p_m\)。令 \(e = |p_i|\),那么 \(e\) 表示经过的第 \(i\) 条边的编号。如果 \(p_i\) 为正数表示从 \(v_e\) 走到 \(u_e\),否则表示从 \(u_e\) 走到 \(v_e\)。
- 如果 \(t = 2\),输出 \(m\) 个整数 \(p_1, p_2, \dots, p_m\),其中 \(p_i\) 表示经过的第 \(i\) 条边的编号。
输入样例
2
5 6
2 3
2 5
3 4
1 2
4 2
5 1
输出样例
YES
4 1 3 5 2 6
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 4e5 + 10;
int type;
int n, m;
int h[N], e[M], ne[M], idx;
bool used[M];
int ans[M], cnt; //ans表示欧拉路径,cnt表示路径上边的数量
int din[N], dout[N]; //点的出度与入度;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u) {
for (int &i = h[u]; ~i;) { //使用引用,可以直接在i=ne[i]中,将边删掉;
if (used[i]) { //如果该条边使用过了,就直接删去,可以防止再次遍历,从而降低复杂度
i = ne[i];
continue;
}
used[i] = true;
if (type == 1) used[i ^ 1] = true; //无向图中的反向边也标记一下;
int t;
if (type == 1) {
t = i / 2 + 1; //转化为边的编号
if (i & 1) t = -t; //如果是反向边
} else t = i + 1;
int j = e[i];
i = ne[i]; //边用过之后直接删了
dfs(j);
ans [ ++ cnt] = t; //从下往上将点输入到路径中,因为从上往下的过程中,可能边路有些环并没有被顾虑到
}
}
int main() {
cin >> type >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ ) {
int a, b;
cin >> a >> b;
add(a, b);
if (type == 1) add(b, a);
din[b] ++ , dout[a] ++ ; //记录入度和出度
}
if (type == 1) {
for (int i = 1; i <= n; i ++ ) {
if ((din[i] + dout[i]) & 1) { //无向图欧拉回路中度数为奇数的点为0;
puts("NO");
return 0;
}
}
} else {
for (int i = 1; i <= n; i ++ ) {
if (din[i] != dout[i]) { //有向图欧拉回路中,入度与出度相同
puts("NO");
return 0;
}
}
}
for (int i = 1; i <= n; i ++ ) { //找到一个不是孤立的点,即有边的点
if (h[i] != -1) {
dfs(i);
break;
}
}
if (cnt < m) { //如果回路中的边数小于总边数,则不构成欧拉回路
puts("NO");
return 0;
}
//因为是逆序将点输入的,所以要逆序将点打出来;
puts("YES");
for (int i = cnt; i; i -- ) cout << ans[i] << ' ';
return 0;
}
动态规划
数字三角形模型
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输入格式
第一行包含整数 \(n\),表示数字三角形的层数。
接下来 \(n\) 行,每行包含若干整数,其中第 \(i\) 行表示数字三角形第 \(i\) 层包含的整数。
输出格式
输出一个整数,表示最大的路径数字和。
输入样例
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例
30
说明
- 状态表示:\(f[i][j]\)表示从左上角到第\(i\)行第\(j\)列的和的最大值
- 转移方程:\(f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i][j]\)
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N];
int f[N][N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
scanf("%d", &a[i][j]);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= i + 1; j ++ )
f[i][j] = -INF;
f[1][1] = a[1][1];
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]); //转移方程
int res = -INF;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]); //最大值在第n层的某一个点取得
printf("%d\n", res);
return 0;
}
最长上升子序列(LIS)
给定一个长度为 \(N\) 的数组,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数 \(N\)。
第二行包含 \(N\) 个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
输入样例
7
3 1 2 1 8 5 6
输出样例
4
说明
- 状态表示:\(f[i]\) 表示以 \(A[i]\) 结尾的最长递增子序列(LIS)的长度
- 转移方程:\(f[i] = \max\limits_{0 \leq j < i, A[j] < A[i]} \{f[j] + 1\}\)
参考代码
朴素版
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) {
f[i] = 1; // 只有a[i]一个数
for (int j = 1; j < i; j ++ )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);// 前一个小于自己的数结尾的最大上升子序列加上自己,即+1
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
printf("%d\n", res);
return 0;
}
单调队列优化
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int q[N]; //长度为i的单调队列以q[i]结尾
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
int len = 0;
for (int i = 0; i < n; i ++ ) { // 从短到长解决各个子串的 LIS
int l = 0, r = len; // 二分搜索,得到能接在 a[i] 前面的上升子序列的最大长度 l
while (l < r) {
int mid = l + r + 1 >> 1;
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
q[r + 1] = a[i]; //一点会变小,否者r + 1才是目标长度
}
printf("%d\n", len);
return 0;
}
最长公共子序列(LCS)
给定两个长度分别为 \(N\) 和 \(M\) 的字符串 \(A\) 和 \(B\),求既是 \(A\) 的子序列又是 \(B\) 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含一个长度为 \(N\) 的字符串,表示字符串 \(A\)。
第三行包含一个长度为 \(M\) 的字符串,表示字符串 \(B\)。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
输入样例
4 5
acbd
abedc
输出样例
3
说明
状态表示:\(f[i][j]\) 表示前缀子串 \(A[1 \sim i]\) 与 \(B[1 \sim j]\) 的最长公共子序列(LCS)的长度。
转移方程:\(f[i][j] = \max \{f[i - 1][j], f[i][j - 1], f[i - 1][j - 1] + 1\}\)
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main() {
scanf("%d%d", &n, &m);
scanf("%s%s", a + 1, b + 1);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ ) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]); //两种转移方法区最大值
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1); //如果可以匹配进行判断
}
printf("%d\n", f[n][m]);
return 0;
}
最长公共上升子序列(LCIS)
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共上升子序列,现在又让他们研究最长公共上升子序列了。
小沐沐说,对于两个序列 \(A\) 和 \(B\),如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个序列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过,只要告诉奶牛它的长度就可以了。
数组 \(A\) 和 \(B\) 的长度均不超过 \(3000\)。
输入格式
第一行包含一个整数 \(N\),表示数组 \(A\),\(B\) 的长度。
第二行包含 \(N\) 个整数,表示数组 \(A\)。
第三行包含 \(N\) 个整数,表示数组 \(B\)。
输出格式
输出一个整数,表示最长公共上升子序列的长度。
输入样例
4
2 2 1 3
2 1 2 3
输出样例
2
说明
状态表示
- \(f[i][j]\) 代表所有 \(a[1 \sim i]\) 和 \(b[1 \sim j]\) 中以 \(b[j]\) 结尾的公共上升子序列的集合;
- \(f[i][j]\) 的值等于该集合的子序列中长度的最大值;
转移方程
首先依据公共上升子序列中是否包含 \(a[i]\),将 \(f[i][j]\) 所代表的集合划分成两个不重不漏的子集:
- 不包含 \(a[i]\) 的子集,最大值是 \(f[i - 1][j]\);
- 包含 \(a[i]\) 的子集,将这个子集继续划分,依据是子序列的倒数第二个元素在 \(b[1]\) 中是哪个数:
- 子序列只包含 \(b[j]\) 一个数,长度是 \(1\);
- 子序列的倒数第二个数是 \(b[1]\) 的集合,最大长度是 \(f[i - 1][1] + 1\);
- 子序列的倒数第二个数是 \(b[j - 1]\) 的集合,最大长度是 \(f[i - 1][j - 1] + 1\);
- ...
然后我们发现每次循环求得的 \(maxv\) 是满足 \(a[i] > b[k]\) 的 \(f[i - 1][k] + 1\) 的前缀最大值。
因此可以直接将 \(maxv\) 提到第一层循环外面,减少重复计算,此时只剩下两重循环。
最终答案取整个子序列结尾最大值即可。
参考代码
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);
for (int i = 1; i <= n; i ++ ) {
int maxv = 1;
for (int j = 1; j <= n; j ++ ) {
f[i][j] = f[i - 1][j];
if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
printf("%d\n", res);
return 0;
}
01背包
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品数量和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i, w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
说明
状态表示:\(f[i][j]\) 表示从前 \(i\) 个物品中选,容量不超过 \(j\) 的最大值。
状态转移:\(f[i][j] = \max \{f[i - 1][j], f[i - 1][j - v[i]] + w[i]\}\)
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]); //从大到小遍历可以省略第一维度
cout << f[m] << endl;
return 0;
}
完全背包
有 \(N\) 种物品和一个容量是 \(V\) 的背包,每种物品都有无限件可用。
第 \(i\) 种物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i, w_i\),用空格隔开,分别表示第 \(i\) 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
多重背包
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
第 \(i\) 种物品最多有 \(s_i\) 件,每件体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行三个整数 \(v_i, w_i, s_i\),用空格隔开,分别表示第 \(i\) 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
朴素版
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m; // n表示物品数量,m表示背包容量
int v[N], w[N], s[N]; // v[i]表示第i个物品的体积,w[i]表示第i个物品的价值,s[i]表示第i个物品的最大数量
int f[N][N]; // f[i][j]表示前i个物品在容量为j时的最大价值
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
// 输入每个物品的体积、价值和数量
for (int i = 1; i <= n; i++)
cin >> v[i] >> w[i] >> s[i];
// 动态规划求解
for (int i = 1; i <= n; i++) // 枚举物品
for (int j = 0; j <= m; j++) // 枚举背包容量
// 枚举当前物品可以选取的数量,确保不超过当前容量j和物品的数量s[i]
for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
// 状态转移方程,选择k个第i个物品的最大价值
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
// 输出背包容量为m时的最大价值
cout << f[n][m] << endl;
return 0;
}
二进制优化
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main() {
cin >> n >> m;
int cnt = 0;
for (int i = 1; i <= n; i ++ ) { //二进制处理
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s) {
cnt ++ ;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0) {
cnt ++ ;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i ++ )//01背包优化+二进制
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);//这里就是f[j]
cout << f[m] << endl;
return 0;
}
单调队列优化
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 20010; // 定义最大容量数组大小
int f[N], g[N], q[N]; // f是dp数组,g是用来暂存的数组,q是单调队列
int n, m; // n是物品数量,m是背包容量
int v, w, s; // v是物品体积,w是物品价值,s是物品数量
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
// 循环处理每一个物品
for (int i = 0; i < n; ++i) {
// 输入每个物品的体积v、价值w、数量s
cin >> v >> w >> s;
// 将当前f数组内容拷贝到g数组,用于之后计算
memcpy(g, f, sizeof f);
// 遍历体积余数为j的所有情况
for (int j = 0; j < v; ++j) {
int hh = 0, tt = -1; // hh和tt是单调队列的头尾指针,初始化为空队列
// 遍历容量从j开始,每次增加v的倍数
for (int k = j; k <= m; k += v) {
// 移动队列头指针,保持队列中的范围不超过s个v的倍数
if (hh <= tt && k - s * v > q[hh]) hh++;
// 保持队列单调性,删除队尾不满足条件的元素
while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt--;
// 将当前k位置加入单调队列
q[++tt] = k;
// 更新f[k],通过队列头的最优值进行转移
f[k] = g[q[hh]] + (k - q[hh]) / v * w;
}
}
}
// 输出结果,即容量为m时的最大价值
cout << f[m] << endl;
return 0;
}
混合背包
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
物品一共有三类:
- 第一类物品只能用 1 次(01 背包);
- 第二类物品可以用无限次(完全背包);
- 第三类物品最多只能用 \(s_i\) 次(多重背包)。
每种体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行三个整数 \(v_i, w_i, s_i\),用空格隔开,分别表示第 \(i\) 种物品的体积、价值和数量:
- \(s_i = -1\) 表示第 \(i\) 种物品只能用 1 次;
- \(s_i = 0\) 表示第 \(i\) 种物品可以用无限次;
- \(s_i > 0\) 表示第 \(i\) 种物品可以使用 \(s_i\) 次。
输出格式
输出一个整数,表示最大价值。
输入样例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出样例
8
参考代码
#include <iostream>
using namespace std;
const int N = 1010; // 定义背包容量数组大小
int n, m; // n表示物品数量,m表示背包容量
int f[N]; // 定义f数组,用于动态规划计算最大价值
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
// 遍历每个物品
for (int i = 0; i < n; i++) {
int v, w, s; // v为物品体积,w为物品价值,s为物品数量
cin >> v >> w >> s;
// 如果是0-1背包(s == 0),即每种物品只能选择一次
if (!s) {
// 采用0-1背包的逆序遍历,从容量m开始倒着计算
for (int j = v; j <= m; j++)
f[j] = max(f[j], f[j - v] + w); // 更新f[j],选择该物品或不选择
}
// 如果是多重背包问题(s > 0 或 s == -1表示完全背包)
else {
if (s == -1) s = 1; // 当s == -1时,将其转换为完全背包,表示物品可以无限选
// 采用二进制优化多重背包,分解物品数量
for (int k = 1; k <= s; k *= 2) {
// 逆序遍历容量,确保每个物品选取的数量不超过当前的限制
for (int j = m; j >= k * v; j--)
f[j] = max(f[j], f[j - k * v] + k * w); // 更新f[j],考虑选择k件该物品的情况
s -= k; // 剩余数量减少k
}
// 处理剩下的数量(不满足二进制分解部分)
if (s) {
for (int j = m; j >= s * v; j--)
f[j] = max(f[j], f[j - s * v] + s * w); // 处理剩下的物品数量
}
}
}
// 输出背包容量为m时的最大价值
cout << f[m] << endl;
return 0;
}
二维费用背包
有 \(N\) 件物品和一个容量是 \(V\) 的背包,背包能承受的最大重量是 \(M\)。
每件物品只能用一次。体积是 \(v_i\),重量是 \(m_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。输出最大价值。
输入格式
第一行三个整数,\(N, V, M\),用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 \(N\) 行,每行三个整数 \(v_i, m_i, w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例
8
参考代码
#include <iostream>
using namespace std;
const int N = 110; // 定义最大容量的常量
int n, V, M; // n表示物品数量,V表示背包的体积限制,M表示背包的重量限制
int f[N][N]; // f数组表示在不同体积和重量下的最大价值
int main() {
// 输入物品数量n、背包体积上限V和重量上限M
cin >> n >> V >> M;
// 遍历每个物品
for (int i = 0; i < n; i++) {
int v, m, w; // v表示物品体积,m表示物品重量,w表示物品价值
cin >> v >> m >> w;
// 逆序遍历体积和重量,确保每个物品只使用一次
for (int j = V; j >= v; j--)
for (int k = M; k >= m; k--)
// 状态转移方程,考虑放入当前物品和不放入物品的最大值
f[j][k] = max(f[j][k], f[j - v][k - m] + w);
}
// 输出体积为V、重量为M时的最大价值
cout << f[V][M] << endl;
return 0;
}
分组背包
有 \(N\) 组物品和一个容量是 \(V\) 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 \(v_{ij}\),价值是 \(w_{ij}\),其中 \(i\) 是组号,\(j\) 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行有两个整数 \(N, V\),用空格隔开,分别表示物品组数和背包容量。
接下来有 \(N\) 组数据:
- 每组数据第一行有一个整数 \(S_i\),表示第 \(i\) 物品组的物品数量;
- 每组数据接下来 \(S_i\) 行,每行有两个整数 \(v_{ij}, w_{ij}\),用空格隔开,分别表示第 \(i\) 组物品的第 \(j\) 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m; // n表示组数,m表示背包容量
int v[N][N], w[N][N], s[N]; // v[i][j]表示第i组第j个物品的体积,w[i][j]表示第i组第j个物品的价值,s[i]表示第i组物品的数量
int f[N]; // f[j]表示容量为j时的最大价值
int main() {
// 输入组数n和背包容量m
cin >> n >> m;
// 输入每组物品的数据
for (int i = 1; i <= n; i++) {
cin >> s[i]; // 第i组的物品数量
for (int j = 0; j < s[i]; j++) {
cin >> v[i][j] >> w[i][j]; // 输入第i组第j个物品的体积和价值
}
}
// 处理每一组的物品
for (int i = 1; i <= n; i++) {
// 遍历背包容量,从大到小逆序遍历
for (int j = m; j >= 0; j--) {
// 遍历当前组的每一个物品
for (int k = 0; k < s[i]; k++) {
// 如果当前物品的体积小于等于当前容量j
if (v[i][k] <= j) {
// 更新f[j],选择是否放入当前物品
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
}
// 输出背包容量为m时的最大价值
cout << f[m] << endl;
return 0;
}
有依赖的背包
有 \(N\) 个物品和一个容量是 \(V\) 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
如果选择物品 5,则必须选择物品 1 和 2。这是因为 2 是 5 的父节点,1 是 2 的父节点。
每件物品的编号是 \(i\),体积是 \(v_i\),价值是 \(w_i\),依赖的父节点编号是 \(p_i\)。物品的下标范围是 \(1 \dots N\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且价值最大。输出最大价值。
输入格式
第一行有两个整数 \(N, V\),用空格隔开,分别表示物品个数和背包容量。
接下来有 \(N\) 行数据,每行数据表示一个物品。
第 \(i\) 行有三个整数 \(v_i, w_i, p_i\),用空格隔开,分别表示物品的体积、价值和依赖的物品编号。如果 \(p_i = -1\),表示根节点。数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例
11
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m; // n表示物品数量,m表示背包容量
int v[N], w[N]; // v[i]表示第i个物品的体积,w[i]表示第i个物品的价值
int h[N], e[N], ne[N], idx; // h为邻接表头,e为边,ne为下一个节点的索引,idx为边的索引
int f[N][N]; // f[i][j]表示选择以i为根的子树,背包容量为j时的最大价值
// 添加一条从a到b的边
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 深度优先搜索,进行树形DP
void dfs(int u) {
// 遍历当前物品u的所有子节点
for (int i = h[u]; ~i; i = ne[i]) { // 循环遍历物品组
int son = e[i]; // 获取子节点
dfs(son); // 递归遍历子节点
// 分组背包的动态规划过程
for (int j = m - v[u]; j >= 0; j--) // 逆序遍历容量
for (int k = 0; k <= j; k++) // 遍历决策,即当前子树的容量k
f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]); // 更新最大价值
}
// 将当前物品u加入背包中
for (int i = m; i >= v[u]; i--) f[u][i] = f[u][i - v[u]] + w[u]; // 加入当前物品
for (int i = 0; i < v[u]; i++) f[u][i] = 0; // 如果当前容量小于物品体积,则价值为0
}
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
memset(h, -1, sizeof h); // 初始化邻接表
int root; // 记录根节点
// 输入每个物品的体积、价值和父节点
for (int i = 1; i <= n; i++) {
int p;
cin >> v[i] >> w[i] >> p;
if (p == -1) root = i; // 如果p为-1,则当前物品为根节点
else add(p, i); // 否则将物品添加到父节点的子节点中
}
// 深度优先搜索,从根节点开始
dfs(root);
// 输出根节点的最大价值
cout << f[root][m] << endl;
return 0;
}
01背包求方案数
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选择的方案数。注意答案可能很大,请输出答案模 \(10^9 + 7\) 的结果。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品数量和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i, w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 \(10^9 + 7\) 的结果。
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例
2
参考代码
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n, m; // n表示物品数量,m表示背包容量
int f[N], g[N]; // f[j]表示容量为j时的最大价值,g[j]表示达到该最大价值的方案数
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
// 初始化f数组为负无穷大,表示没有物品时的状态,g数组记录方案数
memset(f, -0x3f, sizeof f); // 使用一个极小值来初始化f数组
f[0] = 0; // 背包容量为0时的最大价值为0
g[0] = 1; // 背包容量为0时有1种方案
// 遍历每个物品
for (int i = 0; i < n; i++) {
int v, w; // v表示物品体积,w表示物品价值
cin >> v >> w;
// 逆序遍历容量,防止重复使用物品
for (int j = m; j >= v; j--) {
int maxv = max(f[j], f[j - v] + w); // 计算放入或不放入当前物品的最大价值
int s = 0; // s用于记录达到最大价值的方案数
if (f[j] == maxv) s = g[j]; // 如果当前最大价值没有变化,方案数不变
if (f[j - v] + w == maxv) s = (s + g[j - v]) % mod; // 如果放入当前物品后达到最大价值,增加方案数
f[j] = maxv, g[j] = s; // 更新f[j]和g[j]
}
}
// 找到最大价值
int res = 0;
for (int i = 1; i <= m; i++)
if (f[i] > f[res])
res = i;
// 统计达到最大价值的方案数
int sum = 0;
for (int i = 0; i <= m; i++)
if (f[i] == f[res])
sum = (sum + g[i]) % mod;
// 输出达到最大价值的方案数
cout << sum << endl;
return 0;
}
背包求具体方案
有 \(N\) 件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号构成的序列。物品的编号范围是 \(1 \dots N\)。
输入格式
第一行两个整数,\(N, V\),用空格隔开,分别表示物品数量和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i, w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 \(1 \dots N\)。
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例
1 4
参考代码
#include <iostream>
using namespace std;
const int N = 1010;
int n, m; // n表示物品数量,m表示背包容量
int v[N], w[N]; // v[i]表示第i个物品的体积,w[i]表示第i个物品的价值
int f[N][N]; // f[i][j]表示从第i个物品开始,背包容量为j时的最大价值
int main() {
// 输入物品数量n和背包容量m
cin >> n >> m;
// 输入每个物品的体积和价值
for (int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
// 动态规划求解最大价值
for (int i = n; i >= 1; i--) {
for (int j = 0; j <= m; j++) {
// 不选第i个物品
f[i][j] = f[i + 1][j];
// 选第i个物品,确保容量足够
if (j >= v[i])
f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
}
// 输出选择的物品
int j = m;
for (int i = 1; i <= n; i++) {
// 判断当前物品是否被选择
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
cout << i << ' '; // 输出选择的物品编号
j -= v[i]; // 更新剩余的背包容量
}
}
return 0;
}
区间dp
设有 \(N\) 堆石子排成一排,其编号为 \(1, 2, 3, \dots, N\)。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 \(N\) 堆石子合并成一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 \(1\ 3\ 5\ 2\),我们可以先合并 1、2 堆,代价为 4,得到 \(4\ 5\ 2\),又合并 1、2 堆,代价为 9,得到 \(9\ 2\),再合并得到 11,总代价为 \(4 + 9 + 11 = 24\);
如果第二步是先合并 2、3 堆,代价为 7,得到 \(4\ 7\),最后一次合并代价为 11,总代价为 \(4 + 7 + 11 = 22\)。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 \(N\) 表示石子的堆数 \(N\)。
第二行 \(N\) 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
输入样例
4
1 3 5 2
输出样例
22
说明
-
状态表示:\(f[i][j]\) 表示将 \(i\) 和 \(j\) 合并成一堆的方案集合。
-
转移方程:\(f[i][j] = \min\limits_{i \leq k \leq j - 1} \{f[i][k] + f[k + 1][j] + s[j] - s[i - 1]\}\)
参考代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n; // n表示石子的个数
int s[N]; // 前缀和数组,s[i]表示前i堆石子的总和
int f[N][N]; // f[l][r]表示将第l堆石子到第r堆石子合并为一堆的最小代价
int main() {
// 输入石子的堆数n
scanf("%d", &n);
// 输入每堆石子的数量
for (int i = 1; i <= n; i++)
scanf("%d", &s[i]);
// 计算前缀和数组,s[i]表示前i堆石子的总和
for (int i = 1; i <= n; i++)
s[i] += s[i - 1];
// 枚举所有长度为len的区间
for (int len = 2; len <= n; len++) {
// 枚举区间的左端点l
for (int i = 1; i + len - 1 <= n; i++) {
int l = i, r = i + len - 1; // 区间[l, r]
f[l][r] = 1e8; // 初始化为一个很大的数,表示无穷大
// 枚举分割点k,将区间[l, r]分为[l, k]和[k + 1, r]两部分
for (int k = l; k < r; k++)
// 状态转移方程:将[l, k]和[k + 1, r]的最小合并代价 + 合并两部分的代价
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
}
// 输出将1到n堆石子合并为一堆的最小代价
printf("%d\n", f[1][n]);
return 0;
}
环形区间dp
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 \(N\) 颗能量珠。
能量珠是一颗有标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 \(m\),尾标记为 \(n\),后一颗能量珠的头标记为 \(r\),尾标记为 \(n\),则聚合后释放的能量为 \(m \times r \times n\)(Mars 单位),新产生的珠子的头标记为 \(m\),尾标记为 \(n\)。
需要时,Mars 人就用吸盘去往往柱的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的能量量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 \(N = 4\),4 颗珠子的头标记与尾标记依次为 \((2, 3), (3, 5), (5, 10), (10, 2)\)。
我们用记号 \(\oplus\) 表示两颗珠子的聚合操作,\((j \oplus k)\) 表示第 \(j, k\) 两颗珠子聚合后所释放的能量。则第 4、1 两颗珠子聚合后释放的能量为:
这一串项链可以得到优值为 \(710\) 的一个聚合顺序:\(((4 \oplus 1) \oplus 2) \oplus 3 = 10 \times 2 \times 3 + 10 \times 3 \times 5 + 10 \times 5 \times 10 = 710.\)
输入格式
输入的第一行一个正整数 \(N\),表示项链上珠子的个数。
第二行是 \(N\) 个用空格隔开的正整数,所有的数均不超过 1000,第 \(i\) 个数为第 \(i\) 颗珠子的头标记,当 \(i < N\) 时,第 \(i\) 颗珠子的尾标记应该等于第 \(i+1\) 颗珠子的头标记,第 \(N\) 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以以这样的方式:将项链列桌面上,不要出现交叉,随意指定第一颗珠子,然后按指针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 \(E\),为一个最优聚合顺序所释放的总能量。
输入样例
4
2 3 5 10
输出样例
710
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f; // N是数组的大小,INF是无穷大的初始值
int n; // n表示珠子的个数
int w[N]; // w数组表示每堆珠子的能量
int f[N][N]; // f[l][r]表示合并区间[l, r]的最大得分
int main() {
// 输入珠子的堆数n
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> w[i];
w[i + n] = w[i]; // 将环展开成两倍长度的数组,以便处理环形
}
// 枚举区间长度len,从3开始,因为至少需要三个点才能进行匹配
for (int len = 3; len <= n + 1; len++) {
// 枚举区间的左端点l
for (int l = 1; l + len - 1 <= n * 2; l++) {
int r = l + len - 1; // 计算区间的右端点r
// 枚举区间[l, r]中的分割点k,将区间[l, r]分成[l, k]和[k, r]两部分
for (int k = l + 1; k < r; k++) {
// 状态转移方程,选择分割点k的得分,并更新最大得分
f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
}
}
}
// 计算最大得分
int res = 0;
// 枚举所有可能的起点,找到最大得分
for (int l = 1; l <= n; l++)
res = max(res, f[l][l + n]);
// 输出最大得分
cout << res << endl;
return 0;
}
树形dp
Ural 大学有 \(N\) 名职员,编号为 \(1 \sim N\)。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 \(H_i\) 给出,其中 \(1 \leq i \leq N\)。
现在要召开一场周年庆庆宴会,不过,没有职员愿意和直接上司一起参加。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
输入格式
第一行一个整数 \(N\)。
接下来 \(N\) 行,第 \(i\) 行表示第 \(i\) 号职员的快乐指数 \(H_i\)。
接下来 \(N-1\) 行,每行输入一对整数 \(L, K\),表示 \(K\) 是 \(L\) 的直接上司。(注意一下,后一个数是前一个数的父节点,不要搞反)。
输出格式
输出最大的快乐指数。
输入样例
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
输出样例
5
说明
状态表示
- \(f[i][0]\) 表示不选当前节点
- \(f[i][1]\) 表示选当前节点
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010; // 定义最大员工数量
int n; // n表示员工数量
int h[N], e[N], ne[N], idx; // 邻接表存储树结构:h[]为头,e[]为节点,ne[]为下一个节点的索引,idx为边的索引
int happy[N]; // happy[i]表示第i个员工的开心值
int f[N][2]; // f[i][0]表示不选第i个员工时的最大开心值,f[i][1]表示选第i个员工时的最大开心值
bool has_fa[N]; // has_fa[i]标记第i个员工是否有父节点
// 添加边,表示从b到a的从属关系
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 深度优先搜索进行动态规划计算
void dfs(int u) {
f[u][1] = happy[u]; // 如果选中第u个员工,开心值就是他的自身开心值
// 遍历u的所有子节点
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i]; // j为u的一个子节点
dfs(j); // 递归处理子节点
// 如果选中u,那么子节点j不能被选,累加子节点j不被选时的最大开心值
f[u][1] += f[j][0];
// 如果不选u,可以自由选择子节点j是否被选,取最大值
f[u][0] += max(f[j][0], f[j][1]);
}
}
int main() {
scanf("%d", &n); // 输入员工数量
// 输入每个员工的开心值
for (int i = 1; i <= n; i++)
scanf("%d", &happy[i]);
// 初始化邻接表
memset(h, -1, sizeof h);
// 输入n-1条从属关系
for (int i = 0; i < n - 1; i++) {
int a, b;
scanf("%d%d", &a, &b);
add(b, a); // 将b作为a的父节点加入邻接表
has_fa[a] = true; // 标记a有父节点
}
// 找到根节点(没有父节点的员工就是根节点)
int root = 1;
while (has_fa[root]) root++;
// 进行深度优先搜索和动态规划计算
dfs(root);
// 输出根节点的最大开心值,根节点可以选或者不选,取两者中的较大值
printf("%d\n", max(f[root][0], f[root][1]));
return 0;
}
状压dp
给定一张 \(n\) 个点的带权无向图,点从 \(0 \sim n-1\) 标号,求起点 \(0\) 到终点 \(n-1\) 的最短 Hamilton 路径。
Hamilton 路径的定义是从 \(0\) 到 \(n-1\) 不重复地经过每个点恰好一次。
输入格式
第一行输入整数 \(n\)。
接下来 \(n\) 行每行 \(n\) 个整数,其中第 \(i\) 行第 \(j\) 个整数表示点 \(i\) 到 \(j\) 的距离(记为 \(a[i, j]\))。
对于任意的 \(x, y, z\),数据保证 \(a[x, x] = 0\),\(a[x, y] = a[y, x]\) 并且 \(a[x, y] + a[y, z] \geq a[x, z]\)。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
输入样例
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例
18
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N; // N表示最多20个城市,M为2^N,用于状态压缩
int n; // n表示城市数量
int w[N][N]; // w[i][j]表示从城市i到城市j的路程
int f[M][N]; // f[i][j]表示当前在状态i下,最后一个访问的城市是j时的最小总路程
int main() {
// 输入城市数量n
cin >> n;
// 输入每两个城市之间的路程
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> w[i][j];
// 初始化动态规划数组,将所有状态的距离初始化为无穷大
memset(f, 0x3f, sizeof f);
f[1][0] = 0; // 起点是城市0,因此只访问城市0的状态,距离为0
// 枚举所有可能的状态(使用位掩码表示状态)
for (int i = 0; i < 1 << n; i++) { // i表示当前访问过的城市集合,最多是2^n个状态
for (int j = 0; j < n; j++) { // j表示最后一个访问的城市
if (i >> j & 1) { // 判断城市j是否已经在状态i中访问过
for (int k = 0; k < n; k++) { // k表示可能从城市k转移到城市j
if (i >> k & 1) { // 判断城市k是否已经在状态i中访问过
// 更新状态i下,最后一个访问城市为j的最短路径
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
}
}
}
}
}
// 输出最终结果,即访问所有城市的最小路径
cout << f[(1 << n) - 1][n - 1];
return 0;
}
数位dp
科协里最近很流行数字游戏。
某人命名了一种不降数,这种数字必须满足从左到右各位数字呈非下降关系,如 \(123, 446\)。
现在大家决定玩一个游戏,指定一个整数闭区间 \([a, b]\),问这个区间内有多少个不降数。
注意:不降数不能包含前导零。
输入格式
输入包含多组测试数据。
每组数据占一行,包含两个整数 \(a\) 和 \(b\)。
输出格式
每行给出一组测试数据的答案,即 \([a, b]\) 之间有多少不降数。
输入样例
1 9
1 19
输出样例
9
18
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 15;
int f[N][N]; // f[i][j] 表示长度为 i 位且最高位为 j 的单调递增数字的数量
// 初始化动态规划数组
void init() {
// 1 位数中,每个数字只有一种情况
for (int i = 0; i <= 9; i++) f[1][i] = 1;
// 计算所有位数的单调递增数字
for (int i = 2; i < N; i++) { // i 表示数字的位数
for (int j = 0; j <= 9; j++) { // j 表示当前数字的最高位
for (int k = j; k <= 9; k++) { // k 表示前一位数字的最高位
f[i][j] += f[i - 1][k]; // 累加所有可能的位数组合
}
}
}
}
// dp 函数:计算小于等于 n 的满足条件的数字个数
int dp(int n) {
if (!n) return 1; // 特殊情况:如果 n 为 0,返回 1(表示 0 本身)
vector<int> nums;
// 将 n 按照位数拆分并存储到数组 nums 中
while (n) {
nums.push_back(n % 10);
n /= 10;
}
int res = 0; // 存储结果
int last = 0; // 用于记录上一次位的值
// 从最高位开始处理,nums.size() 是数字的总位数
for (int i = nums.size() - 1; i >= 0; i--) {
int x = nums[i]; // 当前位的值
// 统计比当前位小的所有数,符合递增条件
for (int j = last; j < x; j++)
res += f[i + 1][j]; // f[i+1][j] 表示以 j 为最高位,且有 i+1 位的递增数的数量
// 如果当前位的数字比上一次的数字小,则不符合递增条件,停止计算
if (x < last) break;
last = x; // 更新上一位的值
// 如果到达最低位并且所有数字满足条件,则递增数字加 1
if (!i) res++;
}
return res;
}
int main() {
init(); // 初始化动态规划数组
int l, r;
// 输入区间 l 和 r,计算区间内符合条件的数字个数
while (cin >> l >> r)
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
基环树dp
你准备游览一个公园,该公园由 \(N\) 个岛屿组成,当地管理部门从每个岛屿出发向另外一个岛屿建了一座桥,不过桥是可以双向行走的。
同时,每对岛屿之间都有一艘专用的往来两岛之间的渡船。
相对于乘船而言,你更喜欢步行。
你希望经过的桥的总长度尽可能的长,但受到以下的限制:
- 你只能选择一个岛屿开始游览。
- 任何一个岛屿不能游览两次以上。
- 无论任何时间你都可以从你现在所在的岛 \(S\) 走到另一个从未到过的岛 \(D\)。由 \(S\) 到 \(D\) 可以有以下方法:
- 步行:仅当两个岛之间有一座桥才有可能。对于这种情况,桥的长度会累加到你步行的总距离中。
- 渡船:你可以选择这种方法,但当没有任何桥可以前往的岛屿时才可以使用渡船的组合到达 \(S\) 走到 \(D\)(当检查是否可以到达时,你应该考虑所有的路径,包括经过你曾游览过的那些岛)。
注意:你不必游览所有的岛,也可能无法走完所有的桥。
请你编写一个程序,给定 \(N\) 座桥以及它们的长度,按照上述的规则,计算你可以走过的桥的最大长度。
输入格式
- 第一行包含整数 \(N\)。
- 第 \(2\) 到 \(N + 1\) 行,每行包含两个整数 \(a\) 和 \(L\),第 \(i\) 行表示岛屿 \(i\) 上建了一座通向岛屿 \(a\) 的桥,桥的长度为 \(L\)。
输出格式
输出一个整数,表示结果。
对某些测试,答案可能无法放进 \(32-bit\) 整数。
输入样例
7
3 8
7 2
4 2
1 4
1 9
3 4
2 3
输出样例
24
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1200010, M = N * 2;
int n;
int h[N], e[M], w[M], ne[M], idx; //邻接表
int fu[N], fw[N], q[N]; //记录每个点的父节点和它与父节点之间边的权值
int cir[N], ed[N], cnt; //cir 连续的存储所有环,ed 表示每一段环的终点
LL s[N], d[N * 2], sum[N * 2]; //s[i] 表示 i 到所在环第一个点的前缀和, 拆环成链后的新序列、拆环成链后的前缀和数组
bool st[N], ins[N]; //记录每个点是否被搜过,每个点是否在栈中
LL ans; //记录每棵基环树的直径
void add(int a, int b, int c) { //添加边
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs_c(int u, int from) { //找出所有基环树的环
st[u] = ins[u] = true; //标记
for (int i = h[u]; ~i; i = ne[i]) {
if (i == (from ^ 1)) continue;
int j = e[i];
fu[j] = u, fw[j] = w[i];
if (!st[j]) dfs_c(j, i);
else if (ins[j]) { //找到环
cnt ++ ;
ed[cnt] = ed[cnt - 1];
LL sum = w[i];
for (int k = u; k != j; k = fu[k]) {
s[k] = sum;
sum += fw[k];
cir[ ++ ed[cnt]] = k;
}
s[j] = sum, cir[ ++ ed[cnt]] = j;
}
}
ins[u] = false; //弹栈
}
LL dfs_d(int u) { //统计从 u 往下走的最大距离
st[u] = true;
LL d1 = 0, d2 = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (st[j]) continue;
LL dist = dfs_d(j) + w[i];
if (dist >= d1) d2 = d1, d1 = dist;
else if (dist > d2) d2 = dist;
}
ans = max(ans, d1 + d2); //情况 1
return d1;
}
int main() {
scanf("%d", &n);
memset(h, -1, sizeof h); //初始化邻接表
for (int i = 1; i <= n; i ++ ) {
int a, b;
scanf("%d%d", &a, &b);
add(i, a, b), add(a, i, b); //无向边
}
//找出所有基环树的环
for (int i = 1; i <= n; i ++ )
if (!st[i])
dfs_c(i, -1);
memset(st, 0, sizeof st); //清空标记
for (int i = 1; i <= ed[cnt]; i ++ ) st[cir[i]] = true; //标记环上的点
LL res = 0; //记录答案
for (int i = 1; i <= cnt; i ++ ) {
ans = 0;
int sz = 0; //记录环的大小
for (int j = ed[i - 1] + 1; j <= ed[i]; j ++ ) { //找出环中所有点
int k = cir[j];
d[sz] = dfs_d(k);
sum[sz] = s[k];
sz ++ ;
}
//拆环成链
for (int j = 0; j < sz; j ++ )
d[sz + j] = d[j], sum[sz + j] = sum[j] + sum[sz - 1];
//单调队列
int hh = 0, tt = -1;
for (int j = 0; j < sz * 2; j ++ ) {
if (hh <= tt && j - q[hh] >= sz) hh ++ ;
if (hh <= tt) ans = max(ans, d[j] + sum[j] + d[q[hh]] - sum[q[hh]]); //情况2
while (hh <= tt && d[q[tt]] - sum[q[tt]] <= d[j] - sum[j]) tt -- ;
q[ ++ tt] = j;
}
res += ans; //累加答案
}
printf("%lld\n", res);
return 0;
}
基环树森林dp
上帝手中有 \(N\) 种世界元素,每种元素可以限制另外 1 种元素,把第 \(i\) 种世界元素能够限制的那种世界元素记为 \(A[i]\)。
现在,上帝要把它们中的一部分投放到一个新的空间中去建造世界。
为了世界的和平与安宁,上帝希望所有被投放的世界元素都至少有一个能够限制它的世界元素没有被投放。
上帝希望知道,在此前提下,他最多可以投放多少种世界元素?
输入格式
第一行是一个整数 \(N\),表示世界元素的数量。
第二行有 \(N\) 个整数 \(A[1], A[2], \dots, A[N]\)。\(A[i]\) 表示第 \(i\) 个世界元素能够限制的世界元素的编号。
输出格式
一个整数,表示最多可以投放的世界元素的数量。
输入样例
6
2 3 1 3 6 5
输出样例
3
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010, INF = 1e8;
int n;
int h[N], e[N], rm[N], ne[N], idx; //邻接表
int f1[N][2], f2[N][2];
//f[i][0] 表示从 i 为根的子树中选若干个节点,且不选 i 的所有方案的最大值
//f[i][i] 表示从 i 为根的子树中选若干个节点,且选择 i 的所有方案的最大值
bool st[N], ins[N]; //st 记录每个点是否被搜过,ins 记录每个点是否在栈中
int ans; //记录答案
void add(int a, int b) { //添加边
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs_f(int u, int ap, int f[][2]) { //树形 dp 求以 u 根为的子树中必选 ap 的所有方案的最大值
//不选 u
for (int i = h[u]; ~i; i = ne[i]) {
if (rm[i]) continue;
int j = e[i];
dfs_f(j, ap, f);
f[u][0] += max(f[j][0], f[j][1]);
}
//如果 u 必选,则 u 已经被 p 限制,其他子节点可选可不选
if (u == ap) f[u][1] = f[u][0] + 1, f[u][0] = -INF;
else {
//选 u
f[u][1] = -INF;
for (int i = h[u]; ~i; i = ne[i]) {
if (rm[i]) continue;
int j = e[i];
f[u][1] = max(f[u][1], f[u][0] - max(f[j][0], f[j][1]) + f[j][0] + 1);
}
}
}
void dfs_c(int u, int from) { //找出所有基环树的环
st[u] = ins[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) dfs_c(j, i);
else if (ins[j]) { //找到环
rm[i] = 1; //将边 ap -> p 删去
dfs_f(j, -1, f1); //不用边 ap -> p
dfs_f(j, u, f2); //用边 ap -> p(必选 ap,必不选 p)
ans += max(max(f1[j][0], f1[j][1]), f2[j][0]); //累加所有方案的最大值
}
}
ins[u] = false;
}
int main() {
scanf("%d", &n);
memset(h, -1, sizeof h); //初始化邻接表
for (int i = 1; i <= n; i ++ ) {
int a;
scanf("%d", &a);
add(a, i); //有向边
}
//找出所有基环树的环
for (int i = 1; i <= n; i ++ )
if (!st[i])
dfs_c(i, -1);
printf("%d\n", ans);
return 0;
}
插头dp
给你一个 \(n \times m\) 的棋盘,有的格子是障碍,问共有多少条回路满足经过每个非障碍格子恰好一次。
如图,\(n = m = 4\),\((1, 1), (1, 2)\) 是障碍,共有 2 条满足要求的回路。
输入格式
第一行包含两个整数 \(n, m\)。
接下来 \(n\) 行,每行包含一个长度为 \(m\) 的字符串,字符串中只包含 * 和 .,其中 * 表示障碍格子,. 表示非障碍格子。
输出格式
输出一个整数,表示满足条件的回路数量。
输入样例
4 4
**..
....
....
....
输出样例
2
参考代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50000, M = N * 2 + 7;
int n, m, end_x, end_y; //记录最后一个合法格子的位置
int g[20][20]; //地图
int q[2][N]; //q 表示每次滚动的有效状态在哈希表中的下标
int cnt[N]; //cnt 表示每次滚动的有效状态的数量
int h[2][M]; //h 表示滚动哈希表
LL v[2][M]; //v 表示哈希表中每个状态对应的方案数
int find(int cur, int x) { //开放寻址法找 x 的位置,cur 表示当前滚动的位置
int t = x % M;
while (h[cur][t] != -1 && h[cur][t] != x)
if ( ++ t == M)
t = 0;
return t;
}
void insert(int cur, int state, LL w) { //将 state 插入到哈希表中,w 表示 state 的方案数
int t = find(cur, state); //如果哈希表中不存在,说明是一个新状态
if (h[cur][t] == -1) {
h[cur][t] = state, v[cur][t] = w; //插入哈希表
q[cur][ ++ cnt[cur]] = t; //插入队列
}
else v[cur][t] += w; //否则说明已经在哈希表中,直接更新该状态的方案数
}
int get(int state, int k) { // 求第k个格子的状态,四进制的第k位数字
return state >> k * 2 & 3;
}
int set(int k, int v) { // 构造四进制的第k位数字为v的数
return v * (1 << k * 2);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
char str[20];
scanf("%s", str + 1);
for (int j = 1; j <= m; j ++ )
if (str[j] == '.') {
g[i][j] = 1; //1 表示空地,0 表示障碍
end_x = i, end_y = j; //记录最后一个合法格子的位置
}
}
LL res = 0;
memset(h, -1, sizeof h); //初始化哈希表
int cur = 0; //记录当前滚动数组用到第几维
insert(cur, 0, 1); //最开始一条边都没有,状态是 0,方案数是 1
for (int i = 1; i <= n; i ++ ) {
//每次枚举完一整行,我们需要将行末的所有状态转化成行首的状态
//行末是 0.....,行首是 ......0,相当于将每个状态在四进制表示下左移一位
for (int j = 1; j <= cnt[cur]; j ++ )
h[cur][q[cur][j]] <<= 2;
for (int j = 1; j <= m; j ++ ) {
int last = cur; //记录当前行的状态是滚动数组中第几维
cur ^= 1, cnt[cur] = 0;
memset(h[cur], -1, sizeof h[cur]);
for (int k = 1; k <= cnt[last]; k ++ ) {
int state = h[last][q[last][k]]; //记录当前状态
LL w = v[last][q[last][k]];
int x = get(state, j - 1), y = get(state, j); //记录当前格子的左边和上面的状态
if (!g[i][j]) { //如果当前格子是障碍物
if (!x && !y) insert(cur, state, w); //情况 1
} else if (!x && !y) { //情况 2
if (g[i + 1][j] && g[i][j + 1])
insert(cur, state + set(j - 1, 1) + set(j, 2), w);
} else if (!x && y) { //情况 3
if (g[i][j + 1]) insert(cur, state, w);
if (g[i + 1][j]) insert(cur, state + set(j - 1, y) - set(j, y), w);
} else if (x && !y) { //情况 4
if (g[i][j + 1]) insert(cur, state - set(j - 1, x) + set(j, x), w);
if (g[i + 1][j]) insert(cur, state, w);
} else if (x == 1 && y == 1) { //情况 5
for (int u = j + 1, s = 1;; u ++ ) {
int z = get(state, u);
if (z == 1) s ++ ; else if (z == 2) {
if ( -- s == 0) {
insert(cur, state - set(j - 1, x) - set(j, y) - set(u, 1), w);
break;
}
}
}
} else if (x == 2 && y == 2) { //情况 6
//往左找到第一个左端点变成 2
for (int u = j - 2, s = 1;; u -- ) {
int z = get(state, u);
if (z == 2) s ++ ;
else if (z == 1) {
if ( -- s == 0) {
insert(cur, state - set(j - 1, x) - set(j, y) + set(u, 1), w);
break;
}
}
}
} else if (x == 2 && y == 1) { //情况 7
insert(cur, state - set(j - 1, x) - set(j, y), w);
} else if (i == end_x && j == end_y) //情况 8
res += w;
}
}
}
cout << res << endl;
return 0 ;
}
状态机模型
给定一个长度为 \(N\) 的数组,数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 \(k\) 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前卖出持有的股票)。一次买入卖出合为一笔交易。
输入格式
第一行包含整数 \(N\) 和 \(k\),表示数组的长度以及你可以完成的最大交易笔数。
第二行包含 \(N\) 个不超过 10000 的非负整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
输入样例
3 2
2 4 1
输出样例
2
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 110, INF = 0x3f3f3f3f;
int n, m;
int w[N];
int f[N][M][2];//f[i][j][0]代表从前i天中选,共进行了j次交易,当前状态为不持有股票的最大收益
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
memset(f, -0x3f, sizeof f);//要求最大值,先初始化为负无穷
for (int i = 0; i <= n; i ++ ) f[i][0][0] = 0;//不管几天,只要没有交易收益就是0
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ ) {
f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
}
int res = 0;
//最后一天,共交易k次,且最后不持有股票的最大值即为结果
for (int i = 0; i <= m; i ++ ) res = max(res, f[n][i][0]);
printf("%d\n", res);
return 0;
}
斜率优化dp
有 \(N\) 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 \(N\) 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 \(i\) 个任务所需的时间是 \(T_i\)。
另外,在每批任务开始前,机器需要 \(S\) 的启动时间,故执行一批任务所需的时间是启动时间 \(S\) 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。
请为机器规划一个分组方案,使得总费用最小。
输入格式
第一行包含两个整数 \(N\) 和 \(S\)。
接下来 \(N\) 行每行有一对整数,分别为 \(T_i\) 和 \(C_i\),表示第 \(i\) 个任务单独完成所需的时间 \(T_i\) 及其费用系数 \(C_i\)。
输出格式
输出一个整数,表示最小总费用。
输入样例
5 1
1 3
3 2
4 3
2 3
1 4
输出样例
153
参考代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 300010;
int n, s;
LL t[N], c[N]; //时间、费用的前缀和数组
LL f[N]; //设 f[i] 表示前 i 个任务分成若干批执行的最小费用
int q[N]; //队列
int main() {
scanf("%d%d", &n, &s);
//预处理前缀和
for (int i = 1; i <= n; i ++ ) {
scanf("%lld%lld", &t[i], &c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
int hh = 0, tt = 0; //0 也是一种方案,所以最开始队列中有一个 0
q[0] = 0;
for (int i = 1; i <= n; i ++ ) {
int l = hh, r = tt;
while (l < r) { //二分找出队列中一个点 p,使得 p 前面的线段斜率小于 k,p 后面的线段斜率大于 k,即找出最优决策
int mid = l + r >> 1;
if (f[q[mid + 1]] - f[q[mid]] > (t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) r = mid;
else l = mid + 1;
}
int j = q[r]; //二分找出最优决策
f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n]; //状态转移方程
//注意,大数相乘可能超 long long,这里转化为 double 进行比较
while (hh < tt && (double)(f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt - 1]]) >= (double)(f[i] - f[q[tt - 1]]) * (c[q[tt]] - c[q[tt - 1]])) tt -- ;
q[ ++ tt] = i; //将新决策加入队列
}
printf("%lld\n", f[n]);
return 0;
}
STL库函数
vector动态数组
vector<int> a; //新建一个类型为int的vector容器,容器名为a
vector<int> a(10, 1) //可以指定长度,以及初始值
a.size(); //返回数组a的长度
a.clear(); //清空a中的所有元素
a.empty(); //如果a中没有元素返回true, 有则返回false
a.push_back(x); //在a的尾部插入一个元素x
a.pop_back(); //删除a末尾的元素
a.front(); //返回a的第一个元素
a.end(); //返回a的最后一个元素
for (auto &x : a) //用来遍历a中的所有元素
queue队列
queue<int> a; //类型为int, 名字为a
a.size(); //返回a的长度
a.empty(); //如果a中没有元素返回true, 有则返回false
a.push(x); //向队尾追加一个元素
a.front(); //返回对头元素
a.pop(); //弹出队头元素
priority_queue<int, vector<int>, greater<int>> q; //定义优先队列,保证每次去除的元素都为最小值
priority_queue<int> q; //大根堆,取出为最大值
q.top(); //弹出堆顶元素
deque双端队列
deque<int> a; //类型为int, 名称为a
a.size(); //返回队列中元素的个数
a.empty(); //判断队列是否为空
a.push_back(x); //在队尾插入x
a.push_front(x); //在队头插入x
a.pop_back(); //删除队尾元素
a.pop_front(); //删除队头元素
a.front(); //返回队头元素
a.back(); //返回队尾元素
a.clear(); //清空队列中的元素
stack栈
stack<int> a; //类型为int, 名称为a
a.size(); //返回栈中元素的个数
a.empty(); //判断栈是否为空
a.push(x); //在栈顶插入x
a.top(); //返回栈顶元素
a.pop(); //弹出栈顶元素
set
set<int> a; //存储类型为int, 名称为a
set<int, greater<int>> a; //内部元素从大到小
a.insert(x); //向a中插入x
a.erase(x); //删除x
auto it = a.find(x); //返回元素的迭代器
a.count(x); //判断元素是否存在
a.clear(); //清空
for (auto &x : a) //遍历a
map
map<int, int> a; //从小到大,查询类型为int, 返回类型为int
map<int, int, greater<int>> a; //从大到小
a[2] = 1; //默认为0, 增删改同一
a.erase(2); //删除2
auto it = a.find(2); //返回查询元素的迭代器
a.count(2); //判断元素是否存在
a.clear(); //清空
for (auto &[x, y]: a) //遍历,x为第一个数,y为第二个数
string
string s1;
string s2 = "123"; //初始值为"123"
string s3(4, '6'); //初始值为"6666",注(char)类型
s1 == s2; //判断是否相同
string s = s1 + s2; //链接两个字符串
string a = s1.substr(起始下标,字串长度); //取出字符串的子串
int t = a.find(字符串,起始下标); //返回对应下标,不存在返回a.npos 注:O(n^2)慎用
pair
pair<int, long long> a; //第一个值类型为int, 第二个为long long
a.first; //返回第一个值
a.second; //返回第二个值
== //可以直接判断
// 排序按照第一值来判断
// 再多建议直接写结构体
bitset
bitset<10000> a; //长度为10000, 名称为a
a.count(); //返回有多少个1
a.any(); //判断是否至少有一个1
a.none(); //判断是否为全0
a.set(); //把所有位置设置为1
a.reset(); //把所有位置设置为0
a.set(k, v); //把第k位设置为v
可使用操作符: ~, &, |, ^, <<, >>, ==, !=, []
常用函数
lower_bound(); //大于等于x的第一个元素的位置
例 lower_boumd(a.begin(), a.end(), x) - a.begin();
upper_bound(); //大于x的第一个元素的位置
例 upper_bound(a.begin(), a.end(), x) - a.begin();
reverse(); //反转
reverse(a.begin(), a.end());
abs(x); //x的绝对值
exp(x); //以e为底的指数函数
log(x); //以e为底的对数函数
pow(底数, 指数); //幂函数
sqrt(x); //开根号
ceil(x); //上取整
floor(x); //下去整
round(x); //四舍五入
辅助函数
关闭同步流
ios::sync_with_stdio(false);
cin.tie(nullptr);
快读
说明
仅限于读入 \(int\) 型,可以关闭同步流
使用方法
\(int\ x = read();\)
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
return x * f;
}
快写
说明
仅限输出 \(int\) 型,可以关闭同步流,需要自己输出换行
使用方法
\(write(x);\)
void write(int x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
return;
}
随机数
srand(time(0)); //随机数种子
rand(); //给定一个随机数
Lambda表达式
在函数内构建的Lambda表达式,不需要反复传递参数
常规Lambda表达式
auto name = [&](int x) { //返回x%2的值
return x % 2;
}; //注意有分号
递归Lambda表达式
int c;
cin >> c;
auto dfs = [&](auto &&dfs, int x) -> int { //为了正确引用所以使用&&
int res = 0;
if (x & 1) res ++ ;
if (x) res += dfs(dfs, x >> 1);
return res;
}; //注意有分号
cout << dfs(dfs, c); //需要传递函数
debug定义
说明
避免反复写 \(cout\)(偷懒)
#define debug(x) cout << #x << " = " << x << ' ';
下一个全排列
说明
将123变成132
next_permutation(a.begin(), a.end()); //使当前排列增加1
旋序函数
说明
第一个为第一个元素的迭代器,第二个为开始旋转的中间,第三个为结尾
也就是中间变开头,剩余元素依次位移
例
1 2 3 4 5 在进行以下操作后为 3 4 5 1 2
rotate(a.begin(), a.begin() + 2, a.end());
字符串转换
int a = 100;
string s = to_string(a); //把a转换成string类
a = stoi(s) //把string转int类


 浙公网安备 33010602011771号
浙公网安备 33010602011771号