林轩田 机器学习技法 BP算法学习

通过梯度（即导数，相互影响的变化率），来表示误差大小与网络中各个权重的关系。梯度下降（通过修改权重，以最快的速度减小误差值），不断优化权重，这组权重输出得来的结果使误差尽可能小。即模型的输出更接近实际结果。

 

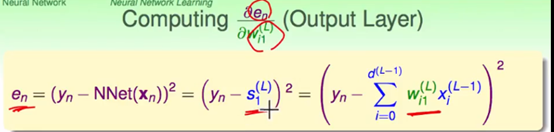
一开始先从最简单的关系入手，即神经网络的最后一层的输出与其实际学习目标的误差关系。

首先根据神经网络计算的式子以及误差的计算公式，将其展开至权重与误差的一个关系式（图中第三个等号后面的式）

是指第L层神经网络根据第L-1层的输出计算后给出的结果 也称为Score

第三个式子中正是将其展开，由L-1层的输出结果各个weight的变换 输出的结果

这个等式正是从权重到输出，到输出与实际数据的误差值的一个关系。

如图正是目标，计算权重与误差的关系。通过一些中间关系，使用链式法则进行展开，展开成以上可以被具体的式子替代掉的形式。如下得到了最后一层的权重与输出误差之间的关系。

接下来，往general的情况考虑，如果是神经网络中任意某一层的weight与误差之间的关系怎么求解？

还是将其根据其定义关系和链式法则 转换成 误差与输出 输出与权重 这样一个式子。输出与权重求导得到的是来自上一层的输出，即这一层神经网络的输入。那最终误差与这层神经网络的输出是什么关系呢？

直接求是得不到的，不像最后一层，有一个输出与学习目标做方差的error进行计算这样一个关系，这里没有一个式子能够直接表示他们之间的一个关系，现将这个不好求的东西封装起来，即error与这层的输出的偏导率关系。记作

 

这个关系不是说不存在，而是并没有那么直接明白的给出，因为神经网络中间的某一层到最后的error隔了可能不止一层，这一层的到最后输出中间隔了几步变换。为了去求解这个关系，就要从这个变换去入手。变换如图；

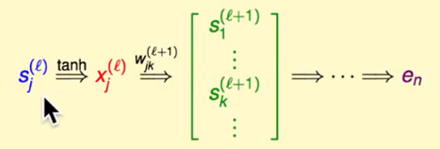
S是上一层的输出，首先经过激活函数非线性映射一下，现在可以直接作为当前层的输入了。在当前层经过一系列(k个)weight的变换，得到一系列的score，即输出。经过这样一层一层的变换，最终到达输出层，进行error的计算。

有了这一系列关系后，可以开始对进行展开了：

如图可见从上一层的输出，到最终这层的输出，与error的关系。

 

 

接下来，将这些关系用其对于的式子进行代换+偏导的求解，从右到左一次是上层输出到这层输入，输入到输出，输出到error的关系，可以看到，这个式子有效的将这层输出与error的关系成功"甩锅"到下一层与错误的关系。

这样做也是符合常理的，因为我这一层作为中间层，的确是不知道最后会导致什么样的误差，只好委托给下一层去，根据之后的最终的误差情况，我才能知道我这一层与error之间的关系。

以上成功建立的一种递推关系。反向传播的过程中（从输出到输入），当前层的error需要从上一层的得到error来计算。如图所示

可以用这个关系一路推下去，将error与weight的关系推到神经网络中的每一次层去，这样就得到了各个层的weight和error的梯度关系，即获取了一个如何通过weight优化error的一个方向。

接下来，将整个BP过程应用于训练算法当中，有以下一些步骤：

1首先随机选择一个数据点，对其跑一次前向计算，得到网络的一个输出，

2通过这个输出，可以和数据点的label计算出error来，

3通过error通过BP计算出各个层的weight与error之间的梯度情况 。

4 使用梯度 梯度下降的方法更新各个weight。 经过N次这样的过程，有这些weight组成的NNet其output的error就越来越小了，即拟合数据中的规律性。

目前广泛使用的一种方法是，取多个点，同时进行以上算法的步骤得到多个梯度，随后将这些梯度进行一个平均值或者什么的，综合一下， 用这个综合的梯度更新weight，可以达到更快地收敛以及更好的拟合效果。