二分图指的是这样一种图,其所有顶点可以分成两个集合X和Y,其中X或Y中任意两个在同一集合中的点都不相连,所有的边关联在两个顶点中,恰好一个属于集合X,另一个属于集合Y。给定一个二分图G,M为G边集的一个子集,如果M满足当中的任意两条边都不依附于同一个顶点,则称M是一个匹配。图中包含边数最多的匹配称为图的最大匹配。
首先来详细了解下概念:
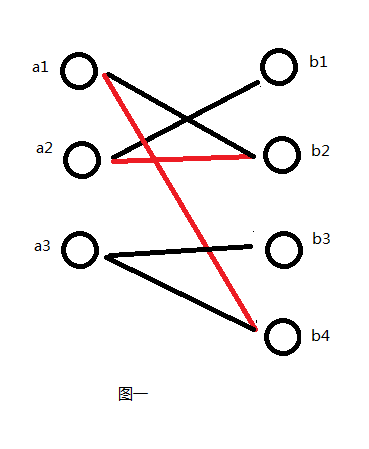
图一就是一个二分图。
匈牙利算法:
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是一种用增广路径求二分图最大匹配的算法。
Hall定理:
二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边,一端恰好为组成X的点的充分必要条件是:X中的任意k个点至少与Y中的k个点相邻。(1≤k≤m)
匹配:
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。图一中红线为就是一组匹配。
未盖点:
设Vi是图G的一个顶点,如果Vi 不与任意一条属于匹配M的边相关联,就称Vi 是一个未盖点。如图一中的a3、b1。
交错路:
设P是图G的一条路,如果P的任意两条相邻的边一定是一条属于M而另一条不属于M,就称P是一条交错路。如图一中a2->b2->a1->b4。
可增广路:
两个端点都是未盖点的交错路叫做可增广路。如图一中的b1->a2->b2->a1->b4->a3。
顶点的数目:
图中顶点的总数。
最大独立数:
从V个顶点中选出k个顶,使得这k个顶互不相邻。 那么最大的k就是这个图的最大独立数。
最小顶点覆盖数:
用最少的顶点数k来覆盖图的所有的边,k就是这个图的最小顶点覆盖数。
最大匹配数:
所有匹配中包含的边数最多的数目称为最大匹配数。
顶点的数目=最大独立数+最小顶点覆盖数(对于所有无向图都有效)
最大匹配数=最小顶点覆盖数(只对二分图有效)
二分图的最大匹配有两种求法,第一种是最大流;第二种就是我现在要讲的匈牙利算法。这个算法说白了就是最大流的算法,但是它跟据二分图匹配这个问题的特点,把最大流算法做了简化,提高了效率。
增广路径的定义(也称增广轨或交错轨):
若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
由增广路径的定义可以推出下述4个结论:
1-P的路径长度必定为奇数,第一条边和最后一条边都不属于M。
2-P上所有第奇数条边都不在M中,所有第偶数条边都出现在M中。
3-P经过取反操作可以得到一个更大的匹配M’。所谓“取反”即把P上所有第奇数条边(原不在M中)加入到M中,并把P中所有第偶数条边(原在M中)从M中删除,则新的匹配数就比原匹配数多了1个。(增广路顾名思义就是使匹配数增多的路径)
4-M为G的最大匹配当且仅当不存在相对于M的增广路径。
最大流算法的核心问题就是找增广路径(augment path)。匈牙利算法也不例外,它的基本模式就是:
初始时最大匹配为空
while 找得到增广路径
do 把增广路径加入到最大匹配中去
可见和最大流算法是一样的。但是这里的增广路径就有它一定的特殊性。(注:匈牙利算法虽然根本上是最大流算法,但是它不需要建网络模型,所以图中不再需要源点和汇点,仅仅是一个二分图。每条边也不需要有方向。)
算法的思路是不停的找增广路径, 并增加匹配的个数,增广路径顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广路径的表现形式是一条"交错路径",也就是说这条由图的边组成的路径, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过。这样交错进行,显然他有奇数条边。那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推。也就是将所有的边进行"反色",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对。另外,单独的一条连接两个未匹配点的边显然也是交错路径。可以证明。当不能再找到增广路径时,就得到了一个最大匹配,这也就是匈牙利算法的思路。
重要结论:
最小点覆盖数: 最小覆盖要求用最少的点(X集合或Y集合的都行)让每条边都至少和其中一个点关联。可以证明:最少的点(即覆盖数)=最大匹配数
const int MAX=1000; int graph[MAX][MAX]; //图,一个二分图,0表示没有边,1表示有 int xN,yN; // 两个点集x,y,每个集合中点的数目 bool checked[MAX]; // 辅助检查,在搜索中表示对应另外一个集合中的点是否被搜索过 //初始化为 false,每一次每个点都要初始化 int match[MAX]; //用于表示一个匹配,说明:y中的某个点对应x中的某个点,例如 match[1]的值是3,说明y中的点1到x中的点3有一条匹配。 // 初始化为 -1,如果是-1表示在某个匹配中这个点未与任何点匹配过, bool searchPath(int u)//注:点集x中的某个点为u,y中的某个点为v { int v; for(v=0;v<yN;v++) { //x中的某个点对y中的每个点进行搜索, if(graph[u][v]==1&&!checked[v]) { checked[v]=true; if(match[v]==-1 || searchPath(match[v])) {//注意理解这个条件是重点。这个条件使用了短路特性 // match[v]==-1 表示 y集合中的v点没有与任何点进行过配对 // searchPath(match[v]) 这里运用了递归解 // 其中意义就是,当match[v]!=-1时(短路特性),对y中v点原来 // 的匹配搜索增广路,如果存在增广路则返回真值。 // 判断语句的主体内容的意义就是。。。 // 如果该点没有被匹配过,或者存在当前匹配,就利用 // 异或操作,让x中的该点(函数参数中的u)与y中的v配对 // 至于其他的?已经在所谓的searchPath函数的递归中进行配对完成了。。 //(集合中称作对称差,A?B=A∪B-A∩B) match[v]=u; return true; } } } //如果没有增广路 return false; } int maxMatch() { int u,matches=0; //下面初始化match的元素为-1 for(int i=0; i<MAX; ++i) { match[i] = -1; } for(u=0;u<xN;u++) {//,点能够一个个加入,应该如何思考呢?博主陷入了深深的沉思 memset(checked,0,sizeof(checked));//每一次加入一个点都要对这个标志进行一次初始化, if(searchPath(u)) matches++; } //所有点都已经顾及, return matches; }




