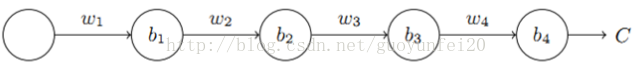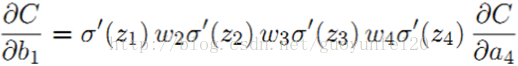转自https://blog.csdn.net/guoyunfei20/article/details/78283043
神经网络中梯度不稳定的根本原因:在于前层上的梯度的计算来自于后层上梯度的乘积(链式法则)。当层数很多时,就容易出现不稳定。下边3个隐含层为例:
其b1的梯度为:
推导过程(参考):https://blog.csdn.net/junjun150013652/article/details/81274958
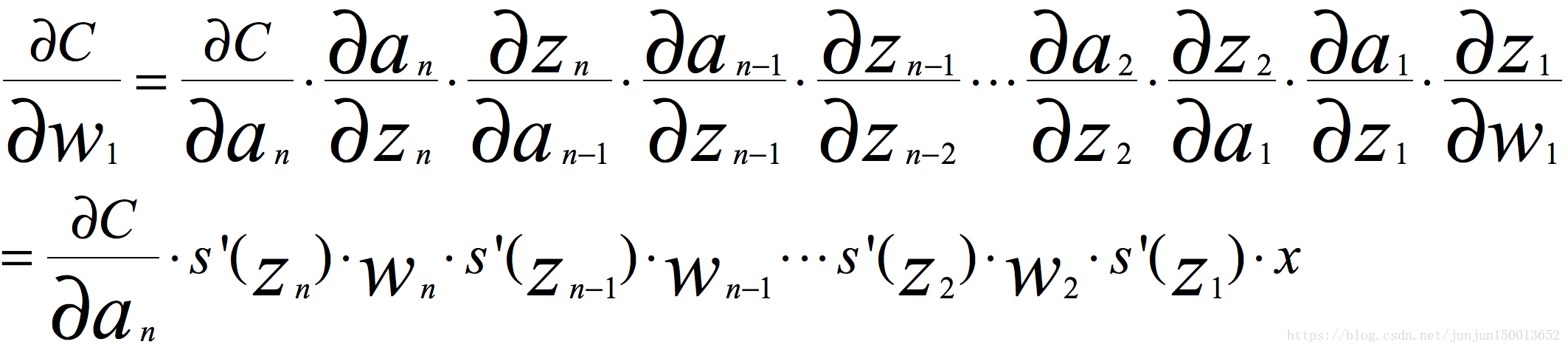
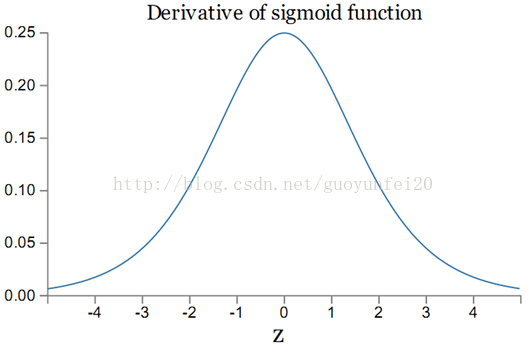
加入激活函数为sigmoid,则其导数如下图:
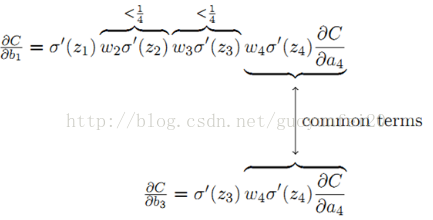
sigmoid导数σ'的最大值为1/4。同常一个权值w的取值范围为abs(w) < 1,则:|wjσ'(zj)| < 1/4,从而有:
从上式可以得出结论:前层比后层的梯度变化更小,变化更慢,进而引起梯度消失的问题。相反,如果|wjσ'(zj)| > 1时,前层比后层的梯度变化更大,就引起梯度爆炸的问题。实际中,当使用sigmoid作为激活函数时,更普遍的是梯度消失的问题。
在重复一遍,从根本上讲无论是梯度消失还是梯度爆炸,其背后的原因是前层网络的梯度是后层网络的乘积,所以神经网络不稳定。唯一可能的情况是以上连续乘积刚好平衡在1左右,但这种几率很小。
解决梯度消失的方法:
隐含层神经元的激活函数用Relu!