反悔贪心总结

一.Olympiad in Programming and Sports - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意：

 　　（2）解题思路

　　　　考虑按编程能力从大到小排序，先选完编程团队中的p个人，然后再考虑体育团队的s人， 考虑维护3个优先队列，一个是a[i]的大根堆，一个是b[i]的大根堆，一个是b[i] - a[i]的大根堆（表示从选择为编程团队转为体育团队的价值），然后取完即可。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct Node {
    int v,id;
    bool operator < (const Node& other) const {
        return v < other.v;
    };
};
int a[N],b[N],Ans[N];
void solve()
{
    int n,s,p;
    cin >> n >> p >> s;
    priority_queue<Node> q[3];
    rep(i,1,n) cin >> a[i];
    rep(i,1,n) cin >> b[i];
    rep(i,1,n) q[0].push({a[i],i});
    int ans = 0;
    while(p) {
        p --;
        auto [v,id] = q[0].top();
        q[0].pop();
        Ans[id] = 1;
        ans += v;
    }
    rep(i,1,n) {
        if(Ans[i]) q[2].push({b[i] - a[i],i});
        else q[1].push({b[i],i});
    }
    while(s) {
        s --;
        while(sz(q[0]) && Ans[q[0].top().id]) q[0].pop();
        while(sz(q[1]) && Ans[q[1].top().id]) q[1].pop();
        int v1 = q[0].top().v,v2 = q[1].top().v,v3 = q[2].top().v;
        if(v2 > v3 + v1) {
            Ans[q[1].top().id] = 2;
            q[1].pop();
            ans += v2;
        }
        else {
            ans += v3 + v1;
            Ans[q[0].top().id] = 1;
            Ans[q[2].top().id] = 2;
            int id = q[0].top().id;
            q[0].pop(),q[2].pop();
            q[2].push({b[id] - a[id],id});
        }
    }
    cout << ans << '\n';
    vector<int> A,B;
    rep(i,1,n) {
        if(Ans[i] == 1) A.pb(i);
        else if(Ans[i] == 2) B.pb(i);
    }
    for(auto x : A) cout << x << ' ';
    cout << '\n';
    for(auto x : B) cout << x << ' ' ;
    cout << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

二.P2949 [USACO09OPEN] Work Scheduling G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

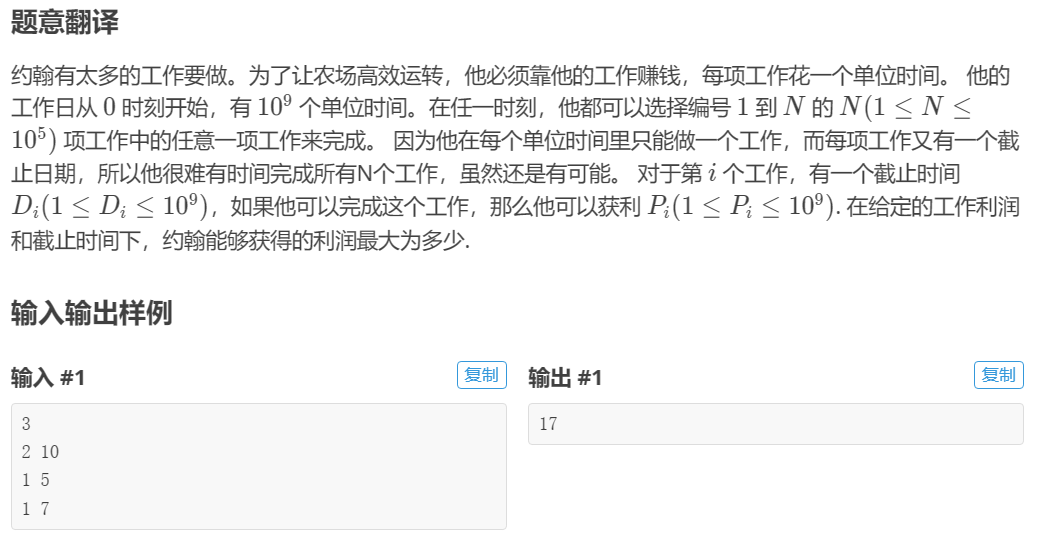
 　　（2）解题思路

　　考虑按截止时间从小到大排序，对于第i个工作的价值，若当前时间小于第i个工作的时间，则可以直接放入优先队列中，否则如果优先队列中有比当前价值小的，则把那个删去，把这个放入优先队列。

　　 （3）代码实现

// Problem: P2949 [USACO09OPEN]Work Scheduling G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2949
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include "bits/stdc++.h"
#define rep(i, z, n) for (int i = z; i <= n; i++)
#define per(i, n, z) for (int i = n; i >= z; i--)
#define ll long long
#define db double
#define PII pair<int, int>
#define fi first
#define se second
#define vi vector<int>
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
using namespace std;
const int N = 1e5 + 10;
struct Work
{
    ll d, p;
} works[N];
void solve()
{
    priority_queue<ll, vector<ll>, greater<ll>> q;
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> works[i].d >> works[i].p;
    }
    sort(works + 1, works + 1 + n, [&](Work &ai, Work &bi) { return ai.d < bi.d; });
    ll ans = 0;
    for (int i = 1; i <= n; i++)
    {
        if (q.size() >= works[i].d)
        {
            if (q.top() < works[i].p)
            {
                ans -= q.top();
                q.pop();
                q.push(works[i].p);
                ans += works[i].p;
            }
        }
        else
        {
            q.push(works[i].p);
            ans += works[i].p;
        }
    }
    cout << ans << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int T = 1;
    // cin >> T;
    while (T--)
        solve();
    return 0;
}

三.P4053 [JSOI2007] 建筑抢修 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

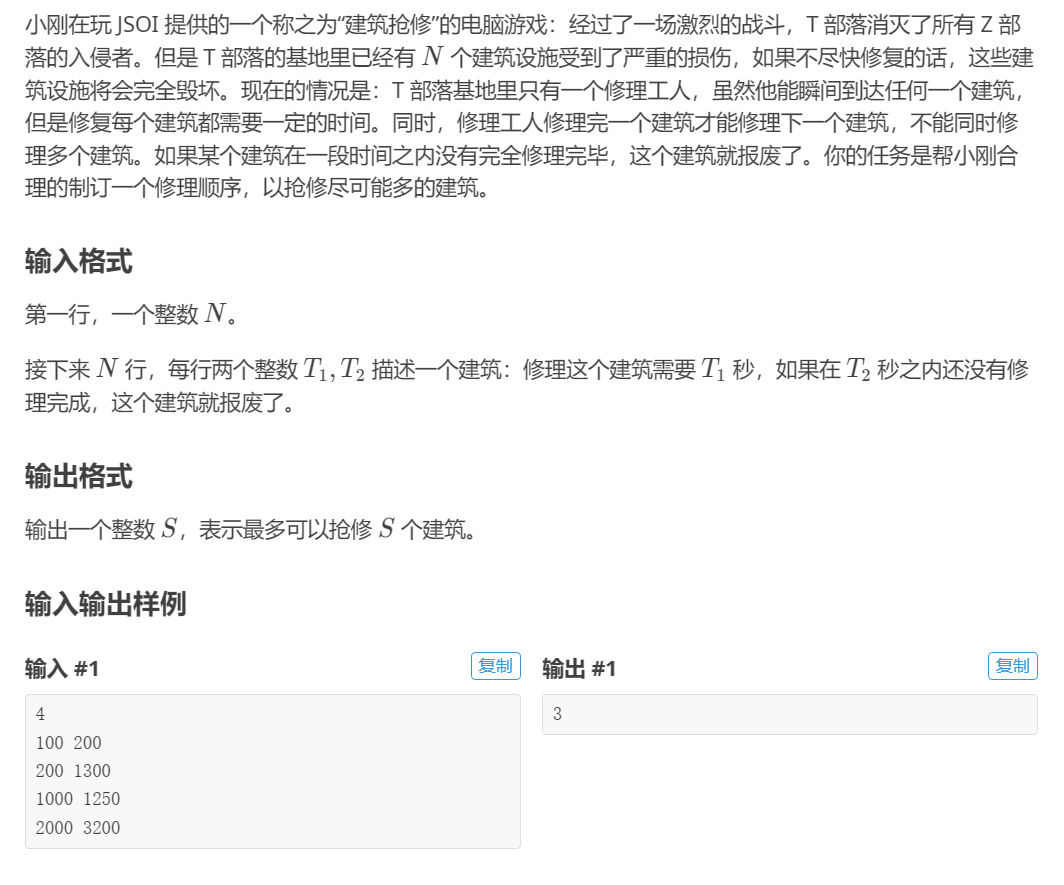
 　　（2）解题思路

　　　　　　和上题类似，直接按截止时间排序，计算即可。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct Work{
    int t1,t2;
    bool operator < (const Work& other) const {
        if(t2 != other.t2) return t2 < other.t2;
        return t1 < other.t1;
    };
}w[N];
void solve()
{
    int n;
    cin >> n;
    ll curTime = 0;
    rep(i,1,n) cin >> w[i].t1 >> w[i].t2;
    sort(w + 1,w + 1 + n);
    priority_queue<int,vector<int>,less<int>> q;
    rep(i,1,n) {
        q.push(w[i].t1);
        curTime += w[i].t1;
        if(curTime > w[i].t2) {
            curTime -= q.top();
            q.pop();
        }
    }
    cout << sz(q) << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

四.P1484 种树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

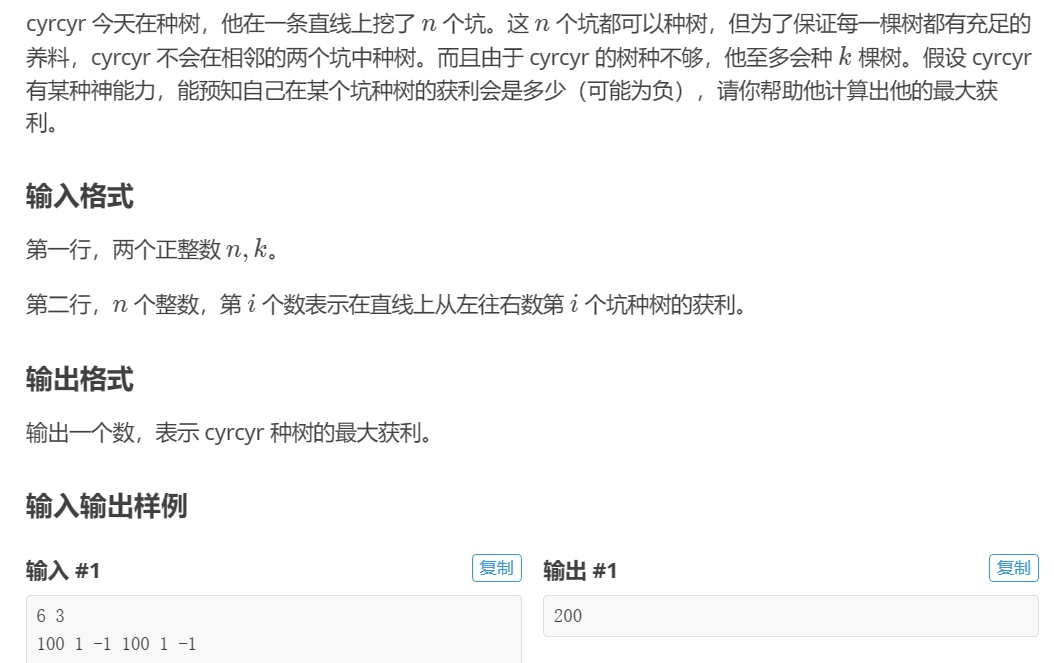
 　　（2）解题思路

　　　　考虑连续三棵树的价值为a,b,c，假如我们选择了b，则反悔获得的价值为a+c-b，又因为会禁用两边的树坑，这个可以用双向链表做到O(1)，用优先队列贪掉k棵即可。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll a[N],L[N],R[N];
bool vis[N];
void solve()
{
    int n,k;
    cin >> n >> k;
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,less<pair<ll,int>>> q;
    rep(i,1,n) {
        cin >> a[i];
        L[i] = i - 1,R[i] = i + 1;
        q.push({a[i],i});
    }
    vis[n + 2] = true;
    ll ans = 0;
    while(k --) {
        int val = 0,idx = n + 2;
        while(sz(q) && vis[idx]) {
            val = q.top().fi;
            idx = q.top().se;
            q.pop();
        }
        if(val <= 0) break;
        ans += val;
        a[idx] = a[R[idx]] + a[L[idx]] - a[idx];
        vis[L[idx]] = vis[R[idx]] = true;
        L[idx] = L[L[idx]];
        R[L[idx]] = idx;
        R[idx] = R[R[idx]];
        L[R[idx]] = idx;
        q.push({a[idx],idx});
    }
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

五.Sequence - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

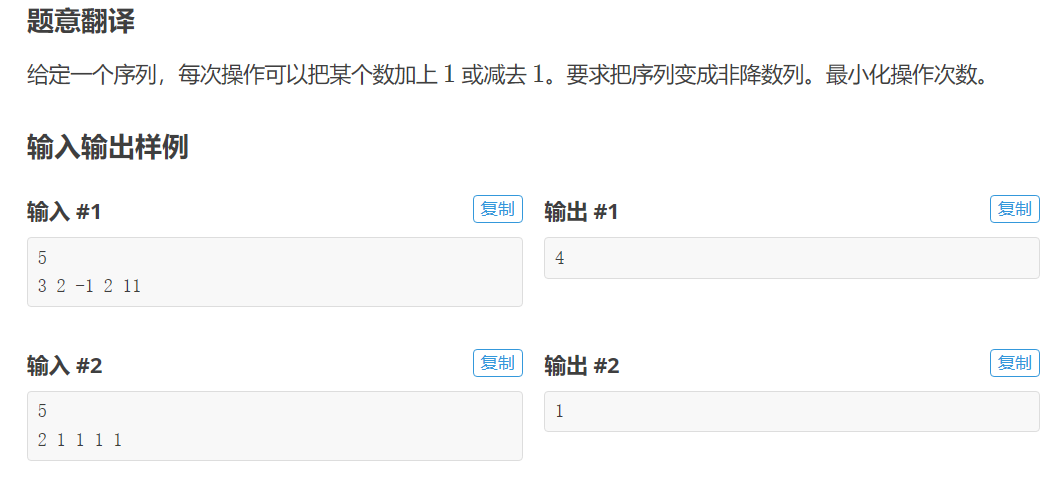
 　　（2）解题思路

　　　　考虑最小化操作次数，有一个结论就是我们最后的每一个数一定是原序列中的一个数，所以我们可以弄一个b数组为原数组的排序后的数组，这题的数据范围为5000，因此可以考虑dp，考虑状态dp[i][j]表示第i个数选择最后变成b数组第j个的最小代价，很明显状态转移可以表示为dp[i][j]=nj~[1,j] min(dp[i-1][nj] + abs(a[j] - b[nj]))。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int a[N],b[N];
ll dp[2][N],mi[N];
const ll inf = 0x3f3f3f3f3f3f3f3f;
void solve()
{
    int n,x;
    cin >> n;
    rep(i,1,n) {
        cin >> a[i];
        b[i] = a[i];
    }
    sort(b + 1,b + 1 + n);
    ll ans = 1e18;
    memset(dp,0x3f,sizeof(dp));
    rep(i,1,n) dp[1][i] = abs(a[1] - b[i]);
    rep(i,2,n) {
        rep(j,0,n) mi[j] = inf;
        rep(j,1,n) mi[j] = min(mi[j - 1],dp[!(i&1)][j]);
        rep(j,1,n) dp[i&1][j] = mi[j] + abs(a[i] - b[j]);
    }
    rep(i,1,n) ans = min(ans,dp[n&1][i]);
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

六.P4597 序列 sequence - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

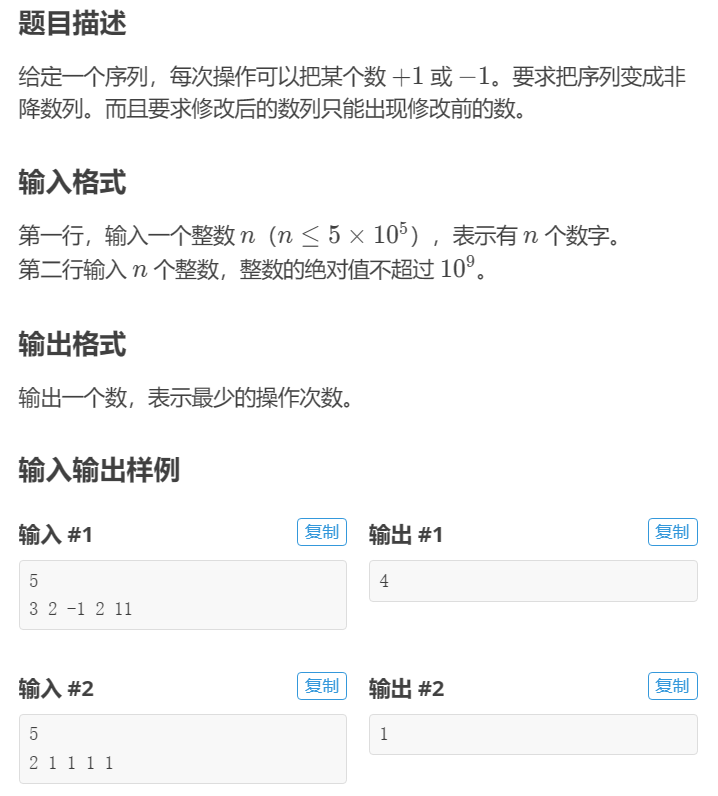
 　　（2）解题思路

　　　　这个是上一个题意得增强版，数据范围变成了5e5，因此考虑贪心，建立大根堆，若当前这个数比堆顶数大，直接放入即可。若当前这个数比堆顶数小，则我们需要加上堆顶数减去当前这个数得贡献，相当于我们这个数变成了[cur,q.top()]这个区间得数，再把堆顶pop掉，把当前数加入队列即可。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
void solve()
{
    int n,x;
    cin >> n;
    ll ans = 0;
    priority_queue<int,vector<int>,less<int>> q;
    rep(i,1,n) {
        cin >> x;
        q.push(x);
        if(x < q.top()) {
            ans += q.top() - x;
            q.pop();
            q.push(x);
        }
    }
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

七.Buy Low Sell High - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

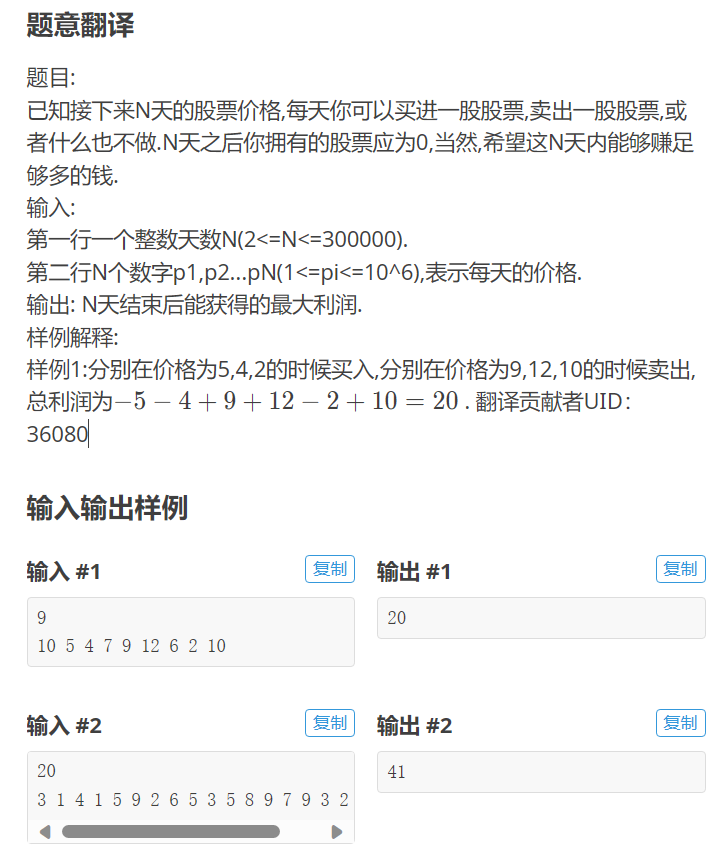
 　　（2）解题思路

　　　　考虑当前这股p[i]卖出，那么就可以获得p[i]-q.top()利润，再把当前这轮放入优先队列即可（反悔得策略，假设是p[i]-p[j],如果后面再来了个p[k],若p[k]匹配到p[j]了，但是p[j]被p[i]匹配了，因此我们放入p[i]则可以得到p[k]-p[i]得获利，再加上p[i]-p[j],就等价于选择p[k]匹配p[i])，每一次都要放入一个p[i]，即表示未反悔得时候买入得股票。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 3e5 + 10;
int p[N];
void solve()
{
    int n;
    cin >> n;
    priority_queue<int,vector<int>,greater<int>> q;
    ll ans = 0;
    rep(i,1,n) {
        cin >> p[i];
        if(sz(q)) {
            if(p[i] > q.top()) {
                ans += p[i] - q.top();
                q.pop();
                q.push(p[i]);
            }
        }
        q.push(p[i]);
    }
    cout << ans << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

八.P2893 [USACO08FEB] Making the Grade G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

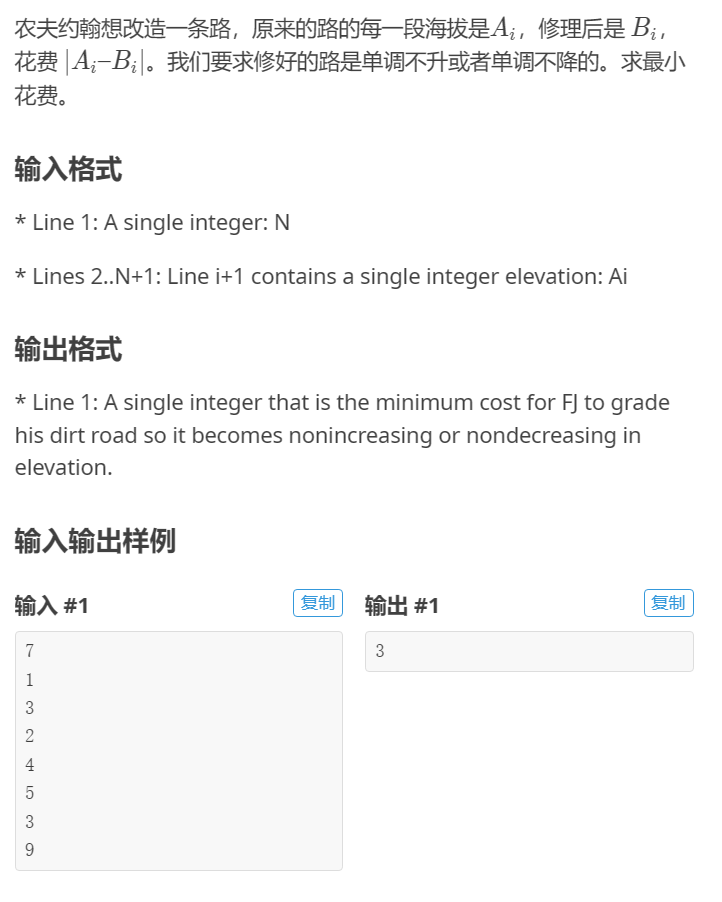
 　　（2）解题思路

　　　　　　和前面题解中得题类似得结论，直接套用结论秒了。

　　 （3）代码实现

　　　　　　

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
void solve()
{
    int n,x;
    cin >> n;
    ll ans1 = 0,ans2 = 0;
    priority_queue<int,vector<int>,less<int>> q;
    priority_queue<int,vector<int>,less<int>> q2;
    rep(i,1,n) {
        cin >> x;
        q.push(x);
        q2.push(-x);
        if(x < q.top()) {
            ans1 += q.top() - x;
            q.pop();
            q.push(x);
        }
        if(-x < q2.top()) {
            ans2 += q2.top() + x;
            q2.pop();
            q2.push(-x);
        }
    }
    cout << min(ans1,ans2) << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

九.P2107 小Z的AK计划 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

 　　（2）解题思路

　　　　和前面一个题套路类似，按位置排序即可，然后贪心做题时间。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct Work {
    ll x,t;
    bool operator < (const Work& other) const {
        if(x != other.x) return x < other.x;
        return t < other.t;
    };
}work[N];
void solve()
{
    ll n,m;
    cin >> n >> m;
    ll curTime = 0;
    rep(i,1,n) cin >> work[i].x >> work[i].t;
    sort(work + 1,work + 1 + n);
    priority_queue<ll,vector<ll>,less<ll>> q;
    rep(i,1,n) {
        curTime += work[i].t;
        q.push(work[i].t);
        if(curTime + work[i].x > m) {
            curTime -= q.top();
            q.pop();
        }
    }
    cout << sz(q) << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

十.P1792 [国家集训队] 种树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

 　　（2）解题思路

　　　　和前面得一个题类似，只不过这个题是个环，那么就特殊处理一下边界就行。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int L[N],R[N],a[N],vis[N];
void solve()
{
    int n,m;
    cin >> n >> m;
    if(m > n / 2) {
        cout << "Error!" << '\n';
        return;
    }
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,less<pair<ll,int>>> q;
    rep(i,1,n) {
        cin >> a[i];
        if(i == 1) L[i] = n;
        else L[i] = i - 1;
        if(i == n) R[i] = 1;
        else R[i] = i + 1;
        q.push({a[i],i});
    }
    vis[n + 2] = true;
    ll ans = 0;
    while(m --) {
        int idx = n + 2;
        ll val = 0;
        while(sz(q) && vis[idx]) {
            idx = q.top().se;
            val = q.top().fi;
            q.pop();
        }
        int Lv = a[L[idx]],Rv = a[R[idx]];
        a[idx] = (Lv + Rv) - a[idx];
        vis[L[idx]] = vis[R[idx]] = true;
        L[idx] = L[L[idx]];
        R[L[idx]] = idx;
        R[idx] = R[R[idx]];
        L[R[idx]] = idx;
        ans += val;
        q.push({a[idx],idx});
    }
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    while(T --) solve();
    return 0;
}

十一.P3620 [APIO/CTSC2007] 数据备份 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

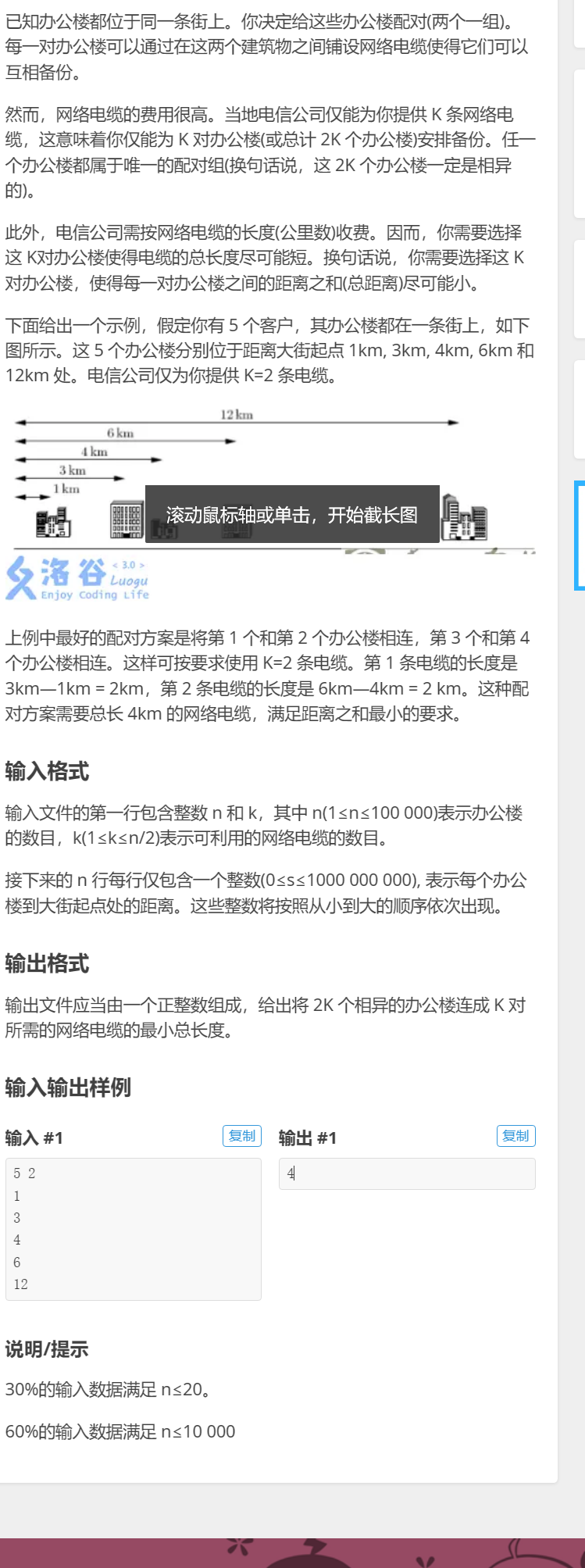
 　　（2）解题思路

　　　　这个题和前面得题有点不相同得讨论，首先最小总长度肯定是相邻着选最优，因此考虑差分配套成相邻得，发现了一个限制，若是选择第i个差分得数，则第i-1个和第i+1个则无法选择，因此转换成了之前<种树>那个题，还有一点不同得是，这里是求最小值，因此应该把边界初始化无穷大。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int pos[N],L[N],R[N];
ll d[N];
bool vis[N];
void solve()
{
    int n,k;
    cin >> n >> k;
    rep(i,1,n) cin >> pos[i];
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q;
    n -= 1;
    rep(i,1,n) {
        L[i] = i - 1;
        R[i] = i + 1;
        d[i] = pos[i + 1] - pos[i];
        q.push({d[i],i});
    }
    d[0] = d[n + 1] = 1e18;
    vis[n + 1] = true;
    ll ans = 0;
    while(k --) {
        ll val = 0,idx = n + 1;
        while(sz(q) && vis[idx]) {
            val = q.top().fi;
            idx = q.top().se;
            q.pop();
        }
        ans += val;
        d[idx] = d[L[idx]] + d[R[idx]] - d[idx];
        vis[L[idx]] = vis[R[idx]] = true;
        L[idx] = L[L[idx]];
        R[L[idx]] = idx;
        R[idx] = R[R[idx]];
        L[R[idx]] = idx;
        q.push({d[idx],idx});
    }
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

十二.Sonya and Problem Wihtout a Legend - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

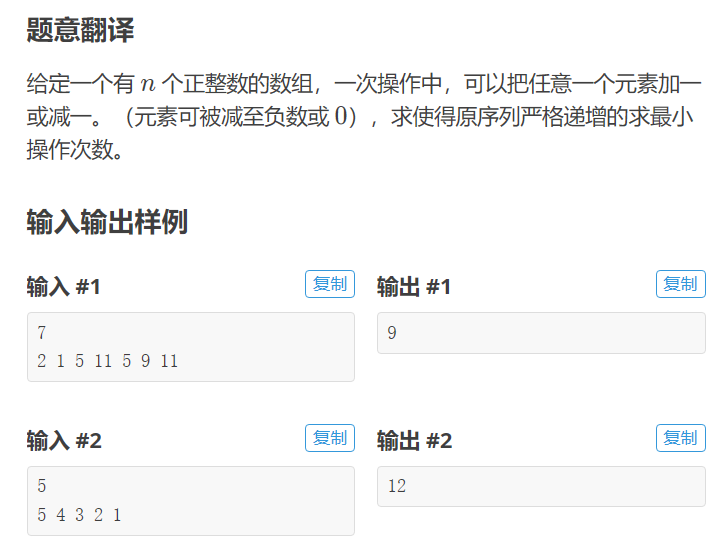
 　　（2）解题思路

　　　　考虑到这个题和前面题目不同得是，这个题要求严格递增，因此我们需要把严格递增转化为不严格递增，我们考虑每一个位置减去i之后，再计算原序列为不严格递增得最小值，再套用上面得反悔贪心即可。

　　（3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int a[N],d[N];
void solve()
{
    ll ans = 0;
    int n;
    cin >> n;
    priority_queue<int,vector<int>,less<int>> q;
    rep(i,1,n) {
        cin >> a[i];
        d[i] = a[i] - i;
    }    
    rep(i,1,n) {
        q.push(d[i]);
        if(d[i] < q.top()) {
            ans += q.top() - d[i];
            q.pop();
            q.push(d[i]);
        }
    }
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

十三.Cardboard Box - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

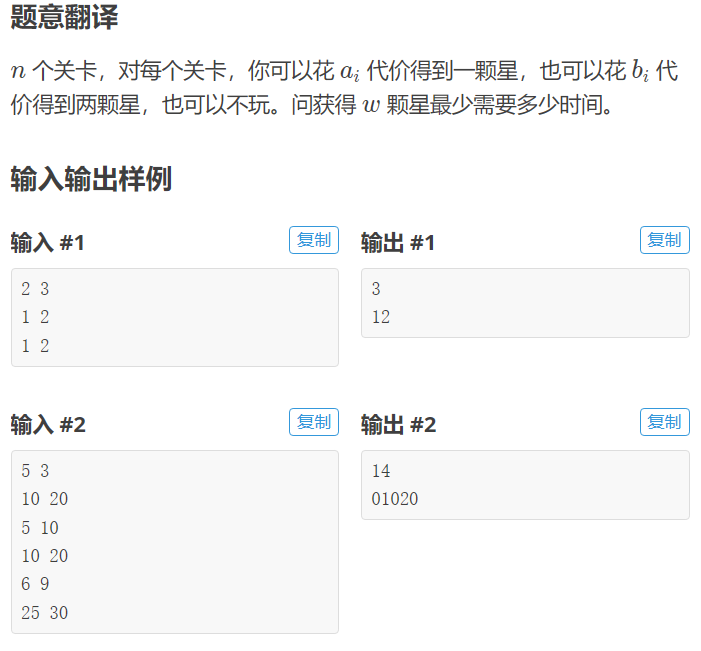
 　　（2）解题思路

　　　　考虑到每一关既可以得一颗星也可以得两颗星，我们考虑每一次得一颗星有哪些方案，再取最优即可。

　　　　

　　　　考虑增加一颗星得方法：
　　　　　　1.从没选的里面选一个一颗星得：a[i]
　　　　　　2.从选得里面把一颗星得升级:b[i] - a[i]
　　　　　　3.从选的里面把一颗星得退掉，然后选择没选得一个两颗星得:b[i] - a[j]
　　　　　　4.从选的里面把两颗星得退成一颗星，然后选择没选得一个两颗星得:a[j] - b[j] + b[i]

　　　　然后用5个优先队列维护一下即可。

　　（3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 3e5 + 10;
int a[N],b[N],Ans[N];
const ll inf = 1e18;
void solve()
{
    // freopen("G:\\in.txt","r",stdin);
    // freopen("G:\\std.txt","w",stdout);
    int n,k;
    cin >> n >> k;
    rep(i,1,n) cin >> a[i] >> b[i];
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q1,q2,q5,q3;
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,less<pair<ll,int>>> q4;
    //q1:没选得里面一颗星得a[i]，q2:没选得里面两颗星得b[i]，q5：选得里面两颗星得a[i] - b[i]
    //q3:选的里面一颗星得b[i]-a[i]  q4：选的里面一颗星的a[i]
    rep(i,1,n) {
        q1.push({a[i],i});
        q2.push({b[i],i});
    }
    ll ans = 0;
    while(k --) {
        int op = -1;
        ll mi = inf;
        while(sz(q1) && Ans[q1.top().se]) q1.pop();
        while(sz(q2) && Ans[q2.top().se]) q2.pop();
        while(sz(q3) && Ans[q3.top().se] != 1) q3.pop();
        while(sz(q4) && Ans[q4.top().se] != 1) q4.pop();
        while(sz(q5) && Ans[q5.top().se] != 2) q5.pop();
        if(sz(q1)) {
            if(mi > q1.top().fi) {
                mi = q1.top().fi;
                op = 1;
            }
        }
        if(sz(q3)) {
            if(mi > q3.top().fi) {
                mi = q3.top().fi;
                op = 2;
            }
        }
        if(sz(q4) && sz(q2)) {
            if(mi > q2.top().fi - q4.top().fi) {
                mi = q2.top().fi - q4.top().fi;
                op = 3;
            }
        }
        if(sz(q5) && sz(q2)) {
            if(mi > q5.top().fi + q2.top().fi) {
                mi = q5.top().fi + q2.top().fi;
                op = 4;
            }
        }
        assert(op != -1);
        ans += mi;
        if(op == 1) {
            auto [val,idx] = q1.top();
            q3.push({b[idx] - a[idx],idx});
            q4.push({a[idx],idx});
            Ans[idx] = 1;
        }
        else if(op == 2) {
            auto [val,idx] = q3.top();
            q5.push({a[idx] - b[idx],idx});
            Ans[idx] = 2;
        }
        else if(op == 3) {
            auto [v1,idx1] = q4.top();
            auto [v2,idx2] = q2.top();
            q1.push({a[idx1],idx1});
            q2.push({b[idx1],idx1});
            q5.push({a[idx2] - b[idx2],idx2});
            Ans[idx1] = 0;
            Ans[idx2] = 2;
        }
        else {
            auto [v1,idx1] = q5.top();
            auto [v2,idx2] = q2.top();
            q3.push({b[idx1] - a[idx1],idx1});
            q4.push({a[idx1],idx1});
            q5.push({a[idx2] - b[idx2],idx2});
            Ans[idx1] = 1;
            Ans[idx2] = 2;
        }
    }
    cout << ans << '\n';
    rep(i,1,n) cout << Ans[i];
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

十三.April Fools' Problem (hard) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

　　（1）题意

 　　（2）解题思路

　　　　考虑到每一天既可以打印也可以准备，又因为每一天得都是花费，但是我们之前做的是一个花费一个收益，所以事情变得困难起来了，考虑把b变成收益，设定一个上界B,则b[i]得收益变为B - b[i],然后按前面讨论贪心获得最大收益即可，不过这题还有一个就是一定要打印k道题，因此我们考虑反悔得时候加入队列得不是真实可加得天数。因为有了收益，我们可以二分上界了，然后计算出一个固定得上界B得情况下满足可以打印k道题，那个时候就是最少花费了。

　　 （3）代码实现

#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int a[N],b[N];
int n,k;
ll ans = 0,bb[N];
int calc(int B)
{
    int cnt = 0;
    ans = 0;
    rep(i,1,n) bb[i] = B - b[i];
    priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q;
    rep(i,1,n) {
        q.push({a[i],1});
        if(sz(q) && bb[i] > q.top().fi) {
            ans += bb[i] - q.top().fi; 
            cnt += q.top().se;
            q.pop();
            q.push({bb[i],0});
        }
    }
    ans = 1ll * k * B - ans;
    return cnt;
}
void solve()
{
    cin >> n >> k;
    rep(i,1,n) cin >> a[i];
    rep(i,1,n) cin >> b[i];
    ll l = 0,r = 2e9;
    while(l <= r) {
        ll m = (l + r) >> 1;
        if(calc(m) < k) l = m + 1;
        else r = m - 1;
    }
    calc(l);
    cout << ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}