关键路径算法（CPM）

一、关键路径算法

　　关键路径算法是在工程能完成的情况下找出关键的几个活动，达到工程更早完成的效果。

二、算法分析

　　这个算法中我们需要用到etv，ltv，ete，lte这几个变量，还需要用到确保工程能完成的算法，也就是拓扑排序算法

　　在这个算法中我们把顶点看作是事件，边权看作是活动持续时间，边看作是活动

　　解释一下这几个变量的含义，etv，ltv（即事件最早开始时间和时间最晚开始时间）

　　　　　　　　　　　　　　　ete，lte（即活动最早开始时间和活动最晚开始时间）

三、算法步骤

　　1.利用拓扑排序求出是否能进行关键路径的查询

　　2.在拓扑排序的过程中求出事件的最早开始时间

　　3.利用栈把拓扑序列存储下来，然后从栈顶依次推出事件的最晚开始时间

　　4.利用ete和lte判断这个活动是否是关键活动

　　5.ete等于这个事件的最早开始时间（为什么？因为你这个事件要想发生，必须等前面的事情全部发生完，所以就是最早开始时间的求解步骤）

　　6.lte等于这个事件的下一个事件的最晚开始时间减去持续时间（为什么？因为下一个事件的最晚开始时间代表着后面的事件能否正常进行，也就是意味着后面的活动是否能进行，同理，最晚活动开始时间也因该是下一个事件的最晚开始时间-持续时间）

四、代码实现

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 int etv[110],ltv[110];//etv是事件最早开始事件，ltv是事件最晚开始事件
 4 int indegree[110];//记录某个顶点的入度
 5 int u[110],v[110],w[110];//建立邻接表
 6 int first[110],outnext[110];
 7 stack <int> Topo;
 8 int n,m;
 9 void TopologicalSort()//进行拓扑排序
10 {
11     int cnt = 0;
12     queue <int> ans;
13     for(int i = 1;i <= n;i++)
14         if(!indegree[i])//把入度为0的点放入队列
15             ans.push(i);
16     while(!ans.empty()){
17         int v1 = ans.front();
18         ans.pop();
19         Topo.push(v1);//把拓扑排序后的序列放入栈，为后面求解最迟事件开始事件做铺垫
20         cnt++;
21         int k =  first[v1];//把他的出边全部遍历
22         while(k != -1){
23             if(!(--indegree[u[k]]))//统计入度为0的点加入拓扑序列
24                 ans.push(u[k]);
25             etv[u[k]] = max(etv[u[k]],etv[v1] + w[k]);//求解事件最早开始时间，为什么需要最大值呢？因为你需要保证前面的事件全部都已经结束，所以你这件事只能在前面几个用时最长的时间做统计
26             k = outnext[k];
27         }
28     }
29     if(cnt < n)//判断是否为拓扑序列
30         cout << "Fail" << endl;
31     else 
32         cout << "Successful!" << endl;
33 }
34 void CriticalPathMethod()
35 {   
36     TopologicalSort();//进行拓扑排序
37     for(int i = 1;i <= n;i++)//因为ltv是求最小值，那么这个数组中的最大也一定是etv中的最大，这样也不会影响ltv的值的求解
38         ltv[i] = etv[n];
39     while(!Topo.empty()){//从汇点（终点）往源点（起点）进行求解ltv（最迟开始时间）
40         int v1 = Topo.top();
41         Topo.pop();
42         int k = first[v1];
43         while(k != -1){
44             ltv[v[k]] = min(ltv[v[k]],ltv[u[k]] - w[k]);//为什么要用min呢？因为你必须得让后面的活动都能够按正常时间进行，所以你不能用最大的，不然后面的工程可能会受到影响
45             k = outnext[k];
46         }
47     }
48     int ete,lte;//ete是活动最早开始时间，lte是活动最晚开始时间。（这里活动指的是边，而事件指的是顶点）
49     for(int i = 1;i <= n;i++){
50         int k = first[i];
51         while(k != -1){
52             ete = etv[i];//活动最早开始时间就是这之前最长的路径，所以也就是事件最早开始时间
53             lte = ltv[u[k]] - w[k];//活动最晚开始时间就是不推迟工期的最晚开工时间，也就是出边的事件的最晚发生时间-这个持续时间（也就是边权）
54             if(lte == ete)//当最早活动开始时间等于最晚活动开始时间时，这个活动就是关键活动，而关键活动的全集就是关键路径，关键路径有可能不止一条
55                 cout << "(" << i << ',' << u[k] << ')' << ":weight" << w[k] << endl;
56             k = outnext[k];
57         }
58     }
59 }
60 int main()
61 {
62     cin >> n >> m;
63     for(int i = 1;i <= n;i++)
64         first[i] = -1;
65     for(int i = 1;i <= m;i++){
66         cin >> v[i] >> u[i] >> w[i];
67         indegree[u[i]]++;//入度+1
68         outnext[i] = first[v[i]];
69         first[v[i]] = i;
70    }
71     CriticalPathMethod();
72     return 0;
73 }

 五、测试数据

test case1　

6 8
1 2 3
1 3 2
2 5 3
2 4 2
3 6 3
4 6 2
5 6 1
3 4 4

answer1

 

 

 

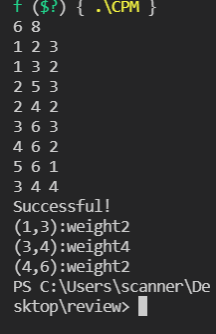
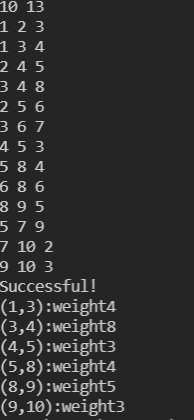
test case2：

10 13
1 2 3
1 3 4
2 4 5
3 4 8
2 5 6
3 6 7
4 5 3
5 8 4
6 8 6
8 9 5
5 7 9
7 10 2
9 10 3

answer2

 

posted @ 2022-02-04 15:36  scannerkk  阅读(1328)  评论(0)  编辑  收藏  举报