数据结构 --- 03.查找, 二叉树

一.查找

　　1.顺序查找(列表无序)

顺序查找原理剖析：
　　从列表中的第一个元素开始，我们按照基本的顺序排序，简单地从一个元素移动到另一个元素，
　　直到找到我们正在寻找的元素或遍历完整个列表。如果我们遍历完整个列表，则说明正在搜索的元素不存在。

def search(alist,item):
    find = False
    length = len(alist)
    
    for i in range(length):
        if alist[i] == item:
            find = True
            
    return find

alist = [3,8,5,7,6,4]
print(search(alist,51))


#False

 

　　2.顺序查找(列表有序)

def search(alist,item):
    length = len(alist)
    find = False
    pos = 0
    stop = False
    while pos <= length and not stop:
        if alist[pos] == item:
            find = True
            break
        elif alist[pos] > item:
            stop = True
        else:
            pos += 1
    return find

alist = [1,3,5,7,9,11]
print(search(alist,5))

#True

 

　　3.二分查找(重要)

　　有序列表对于我们的实现搜索是很有用的。在顺序查找中，当我们与第一个元素进行比较时，
如果第一个元素不是我们要查找的，则最多还有 n-1 个元素需要进行比较。 二分查找则是
从中间元素开始，而不是按顺序查找列表。 如果该元素是我们正在寻找的元素，我们就完成
了查找。 如果它不是，我们可以使用列表的有序性质来消除剩余元素的一半。如果我们正在
查找的元素大于中间元素，就可以消除中间元素以及比中间元素小的一半元素。如果该元素在
列表中，肯定在大的那半部分。然后我们可以用大的半部分重复该过程，继续从中间元素开始，
将其与我们正在寻找的内容进行比较

 

def search(alist,item):
    last = len(alist)-1
    first = 0
    find = False
    
    while first<=last and not find:
        mid = (last+first) // 2
        if alist[mid] == item:
            find = True
        else:
            if alist[mid] > item:
                last = mid - 1
            else:
                first = mid + 1
    return find

alist = [1,3,5,7,9]
print(search(alist,31))

# False

 

二.二叉树

二叉树
　　- 跟节点
　　- 左叶子节点
　　- 右叶子节点
　　- 子树

二叉树遍历
　　广度遍历：层级遍历
　　深度遍历
　　　　前序：根左右
　　　　中序：左根右
　　　　后序：左右根
排序二叉树

 

 

 

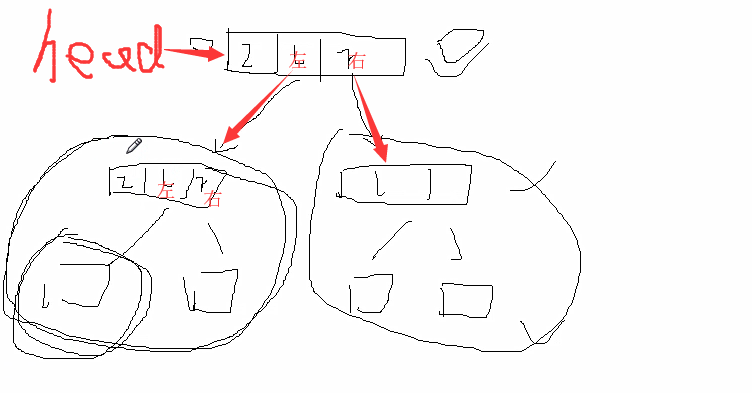
　　1.二叉树的创建及广度遍历

class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None

class Tree():
    #构造方法可以构造一个空树
    def __init__(self):
        self.root = None
    def add(self,item):
        node = Node(item)
        #判断树为空
        if self.root == None:
            self.root = node
            return
        #树为非空的插入操作,创建一个可操作的列表
        queue = [self.root]
        
        while queue:
            cur = queue.pop(0)
            if cur.left == None:
                cur.left = node
                return
            else:
                queue.append(cur.left)
            if cur.right == None:
                cur.right = node
                return
            else:
                queue.append(cur.right)
    #广度遍历
    def travel(self):
        queue = [self.root]
        while queue:
            cur = queue.pop(0)
            print(cur.item)
            if cur.left is not None:
                queue.append(cur.left)
            if cur.right is not None:
                queue.append(cur.right)

tree = Tree()
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
tree.add(10)
tree.travel()

# 1 2 3 4 5 6 7 8 9 10

 

　　2.深度遍历

class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None

class Tree():
    #构造方法可以构造一个空树
    def __init__(self):
        self.root = None
    def add(self,item):
        node = Node(item)
        #判断树为空
        if self.root == None:
            self.root = node
            return
        #树为非空的插入操作
        queue = [self.root]
        
        while queue:
            cur = queue.pop(0)
            if cur.left == None:
                cur.left = node
                return
            else:
                queue.append(cur.left)
            if cur.right == None:
                cur.right = node
                return
            else:
                queue.append(cur.right)

    #深度遍历
    def forward(self,root): #根左右
        if root == None:
            return
        print(root.item,end=' ')
        self.forward(root.left)
        self.forward(root.right)
        
    def mid(self,root):#左根右
        if root == None:
            return
        self.mid(root.left)
        print(root.item,end=' ')
        self.mid(root.right)
        
    def back(self,root):#左右根
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item,end=' ')

tree = Tree()
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
tree.add(10)

tree.forward(tree.root)
print('\n')
tree.mid(tree.root)
print('\n')
tree.back(tree.root)
print('\n')

 

结果为:

1 2 4 8 9 5 10 3 6 7 

8 4 9 2 10 5 1 6 3 7 

8 9 4 10 5 2 6 7 3 1 

 

　　3.排序二叉树

class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None
class Tree():
    #构造方法可以构造一个空树
    def __init__(self):
        self.root = None
    #需要根据一个准则将节点进行插入,准则：比根节点小的数据插入到左侧，比根节点大的数插入到右侧
    def insert(self,item):
        node = Node(item)
        if self.root == None:
            self.root = node
            return
        cur = self.root
        #右
        while True:
            if item > cur.item:
                if cur.right == None:
                    cur.right = node
                    return
                else:
                    cur = cur.right

            else:
                if cur.left == None:
                    cur.left = node
                    return
                else:
                    cur = cur.left
        
     #深度遍历
    def forward(self,root): #根左右
        if root == None:
            return
        print(root.item,end=' ')
        self.forward(root.left)
        self.forward(root.right)
        
    def mid(self,root):#左根右
        if root == None:
            return
        self.mid(root.left)
        print(root.item,end=' ')
        self.mid(root.right)
        
    def back(self,root):#左右根
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item,end=' ')

tree = Tree()
tree.insert(3)
tree.insert(0)
tree.insert(2)
tree.insert(9)
tree.insert(1)
tree.insert(6)
tree.insert(4)
tree.forward(tree.root)
print('\n')
tree.mid(tree.root)
print('\n')
tree.back(tree.root)
print('\n')