Manacher算法详解

目录

• Manacher算法
  • 问题：

Manacher算法

Manacher算法，是用来解决有关回文串的问题的算法。

问题：

给定一个字符串\(S\),长度为\(n\)，求它的最长回文子串的长度？
\(1\leq n\leq 1.1\times 10^7\)

先不讲正解是什么，先想想暴力怎么做。
不难想到我们可以直接枚举中间点然后左右扩展，判一下奇偶就可以了。复杂度\(O(n^2)\)。
我们可以考虑一下优化。
在原字符串的首尾和每个字符中间增加 原字符串中没有的字符 ，比如说\(\%\)，这样就可以不必枚举奇偶了。
举个栗子，字符串\(abc\)在加上\(\%\)之后会变成\(\%a\%b\%c\%\)，\(abcd\)加上之后会变成\(\%a\%b\%c\%d\%\)，字符串长度就都是奇数了。
以字符串\(12212321\)为例，经过上一步，变成了\(S=\%1\%2\%2\%1\%2\%3\%2\%1\%\)
我们设置辅助数组\(p[i]\)来记录以字符\(S[i]\)为中心的最长回文子串向左/右扩张的长度（包括\(S[i]\)），下面的图片中用#代替 \(\%\)。

通过观察我们不难看出\(p[i]-1\)就是以\(S[i]\)为中心的回文子串的长度。其实这东西证明也是很简单的。
假设我们\(p[i]=3\)，然后假设从\(s[i]\)往右的\(3\)个字符为\(\%a\%\)，因为\(p\)数组保留的是半径，所以我们还原该回文串之后就是\(\%a\%a\%\)。
因为\(\%\)都是我们补充的，所以在半径中除去\(\%\)再乘\(2\)就是实际回文串的长度。而求实际在原字符串中的字符个数又有两种情况。

1. 回文串中心是\(\%\)上面我们已经讨论过了，这里就不重复说了。
2. 回文串中心是原字符串中的字符。举个栗子\(a\%a\%(p[i]=4)\)，显然这里的有用的字符就是\(aa\)，因为这是半径，所以我们还要乘\(2\)，但是由于该回文串的中心是原字符串中的字符，所以中间那个字符会算两次，所以我们还要减去中间的那个字符，即\(2\times2-1\)，也就是\(4-1\)，也就是\(p[i]-1\)了。

但是我们还要考虑一点，我们上面讨论的都是结尾字符以\(\%\)的情况，那会不会结尾字符有原字符串中的字符呢？
答案显然是 不可能 的，因为如果有这种情况的话，我们可以再往两边扩展一个\(\%\)（每两个字符中间都有一个\(\%\)），就变成了上面我们讨论的两种情况了。
\(\cdot\) 再设置两个辅助变量
设\(id\)为当前我们已知的右边界最大的回文子串的中心，\(mx\)为\(id+p[id]\)也就是最大的右边界。如下图。

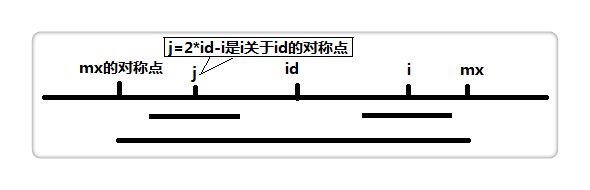
假设我们当前要求的位置为\(i(i<mx)\)，我们可以找到\(i\)关于\(id\)的对称点\(j\)，因为\(id\)为中点，所以\(id\)左侧和右侧字符是 完全一样 的。
所以我们可以利用\(j\)来加速\(p[i]\)的求解。因为\(p[i]\)是可以等于\(p[j]\)的。
但是我们注意到，\(mx\)右边的部分是有可能不等于\(id-p[id]\)（即\(mx\)的对称点）的左边部分的。所以\(p[i]\)应该小于等于\(mx-i\)。至于\(mx\)右侧的部分，我们就只能暴力扩展了。
如果\(i \geq mx\)的话，那我们就只能先暂令\(p[i]=1\)然后同样暴力扩展了。扩展完之后更新\(mx\)和\(id\)。
模板题Manacher算法 下面放代码，代码中用#代替\(\%\)。

#include<bits/stdc++.h>
using namespace std;
char s[32000005],s_new[32000005];
int p[32000005];
int get() {
	s_new[0]='$';
	s_new[1]='#';
	int k=2;
	int n=strlen(s);
	for(int i=0; i<n; i++) {
		s_new[k++]=s[i];
		s_new[k++]='#';
	}
	s_new[k]='\0';
	return k;
}
void manacher() {
	int len=get();
	int mx=0,id=0,ans=-1;
	for(int i=1; i<=len; i++) {
		if(i<mx)
			p[i]=min(mx-i,p[2*id-i]);
		else
			p[i]=1;
		while(s_new[i-p[i]]==s_new[i+p[i]])
			p[i]++;
		if(i+p[i]>mx) {
			mx=i+p[i];
			id=i;
		}
		ans=max(ans,p[i]-1);
	}
	printf("%d\n",ans);
}
int main() {
	scanf("%s",s);
	manacher();
	return 0;
}