LeetCode #1143 Longest Common Subsequence
Question
Given two strings text1 and text2, return the length of their longest common subsequence.
A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, "ace" is a subsequence of "abcde" while "aec" is not). A common subsequence of two strings is a subsequence that is common to both strings.
If there is no common subsequence, return 0.
动归经典问题,最长公共子序列(LCS),注意是子序列而不是子串
Example 1:
Input: text1 = "abcde", text2 = "ace" Output: 3 Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2:
Input: text1 = "abc", text2 = "abc" Output: 3 Explanation: The longest common subsequence is "abc" and its length is 3.
Example 3:
Input: text1 = "abc", text2 = "def" Output: 0 Explanation: There is no such common subsequence, so the result is 0.
动态规划法
先确定状态(或最优子结构),c(i, j)表示str1中前i个字符和str2中前j个字符中的最长公共子序列的长度
可以举一个例子思考来写出状态转移方程:
当 str1[i] == str2[j],c(i, j) = c(i-1, j-1) + 1
当 str1[i] != str2[j],c(i, j) = max(c(i, j-1), c(i-1, j))
当 i == 0 或 j == 0 时,若 str1[i] == str2[j],c(i, j) = 1;str1[i] != str2[j],c(i, j) = 0 (边界条件)
(这个是“或”而不是“和”,非常重要,第一次写的时候就搞错了)
以 str1 = "ABCBDAB", str2 = "BDCABA" 为例来说明枚举的顺序
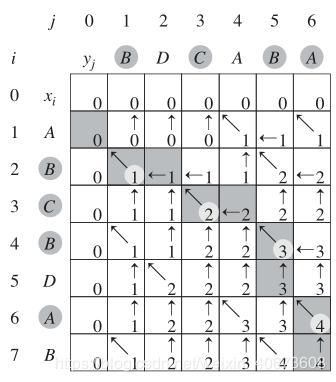
箭头表示“source”,因此填表顺序可以为从上到下,从左到右
从图中可知,边界条件并不只是左上角,而是最上面一条边和最左边一条边
(其实我的算法和这个图是有区别的,这个图将index=0表示为空串了,而我的算法将index=0表示第一个字符)
class Solution: def longestCommonSubsequence(self, text1: str, text2: str) -> int: len_1 = len(text1) len_2 = len(text2) dp = [[0 for j in text2] for i in text1] for i in range(len_1): for j in range(len_2): if (i == 0 or j == 0) and text1[i] == text2[j]: dp[i][j] = 1 elif text1[i] == text2[j]: dp[i][j] = dp[i-1][j-1] + 1 else: dp[i][j] = max(dp[i][j-1], dp[i-1][j]) # print(dp[i][j], text1[i], text2[j]) return dp[len_1-1][len_2-1]
时间复杂度为O(n*m)
打印路径:
定义一个全局变量flag[i][j]用于记录每次的路径是“source”来自左上角/左边/上边,再用一个输出函数递归地打印出来(可参考下方链接)
参考:
https://www.cnblogs.com/wkfvawl/p/9362287.html (以该题为例从某角度理解动态规划)



