Codeforces Round #427 (Div. 2) D dp

D. Palindromic characteristics

题意：求给定字符串每阶回文子串有多少个。

tags：根本没想到 dp。。直接看官方题解吧

dp[i][j] 代表第 i 个字符到第 j 个字符的子串是几阶回文。

Solution.

Let's calculate the following dp.

• dp[l][r] is the maximum k such that the substring built from characters from l to r is k-palindrome.
• The dynamics is calculated in the order of non-decreasing of substring lengths.
• The values for l = r and l = r - 1 are computed trivially.
• Let r - l > 1. Then, if s[l] ≠ s[r] or dp[l + 1][r - 1] = 0, dp[l][r] = 0. Otherwise dp[l][r] = dp[l][m] + 1, where .

When we have dp values, we can calculate cnt[k] — the number of substrings, which dp value is k. Then the number of substrings that are k-palindromes is .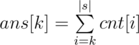

The solution works in O(|s|²) time and uses O(|s|²) memory.

Also, you could notice that the string can be no more than 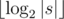-palindrome, and solve the problem in time, reducing the memory usage to O(|s|).

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define rep(i,a,b) for (int i=a; i<=b; ++i)
#define per(i,b,a) for (int i=b; i>=a; --i)
#define mes(a,b)  memset(a,b,sizeof(a))
#define INF 0x3f3f3f3f
#define MP make_pair
#define PB push_back
#define fi  first
#define se  second
typedef long long ll;
const int N = 5005;

int dp[N][N], ans[N];
char s[N];
int main()
{
    scanf("%s", s+1);
    int n = strlen(s+1);
    rep(len,1,n) for(int i=1; i+len-1<=n; ++i)
    {
        int j = i+len-1;
        if(len==1) dp[i][j]=1;
        else if(len==2) dp[i][j]= s[i]==s[j] ? 2 : 0;
        else if(dp[i+1][j-1]==0 || s[i]!=s[j]) dp[i][j]=0;
        else dp[i][j]=dp[i][i+len/2-1]+1;
        ++ans[dp[i][j]];
    }
    per(i,n-1,1) ans[i] += ans[i+1];
    rep(i,1,n) printf("%d ", ans[i]);
    puts("");

    return 0;
}