2017-03-17 Codeforces 441D 置换群,好题 bzoj 4750 思维,按位计算

Codeforces 441D

题意：定义理想序列a[]：对于任意的i有a[i] = i。给出一个1到n的排列p[]，可以将排列中的任意两个元素两两交换，定义f(p)为将p变为理想排列的最少交换次数，求将p变成排列q，使得f(q) = m 的最少交换次数和交换方案。

tags：才知道置换群，看题解码的。。

使得一个排列有序的最小交换次数 = n - 置换群数目。

置换群，A->B，B->C，C->A，相当于一个轮换。   记住三点：

1、一个大小为L的置换群里面的元素至少且必能互换L-1次得到原始排列。

2、分别任取两个置换群的元素交换一次将合并成一个置换群。

3、在一个置换群里面任取两个元素交换一次将分裂成两个置换群。

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define rep(i,a,b) for (int i=a;i<=b;i++)
#define per(i,b,a) for (int i=b;i>=a;i--)
#define mes(a,b)  memset(a,b,sizeof(a))
#define INF 0x3f3f3f3f
#define PII pair<int,int>
#define PB push_back
typedef long long ll;
const int N = 200005;

vector<int >s[N], tmp;
int cnt, n, m, a[N];
bool vis[N];
void cal()    // 计算出置换群数目 cnt 
{
    cnt=0;    mes(vis, 0);
    rep(i,1,n) if(vis[i]==0) {
        int t=i;
        s[cnt].clear();
        while(vis[t]==0) {
            vis[t]=1;
            s[cnt].PB(t);
            t=a[t];
        }
        cnt++;
    }
    rep(i,0,cnt-1) sort(s[i].begin(), s[i].end());
}
int main()
{
    scanf("%d", &n);
    rep(i,1,n) scanf("%d", &a[i]);
    cal();
    int op=n-cnt;    // op为当前序列变为理想序列所需次数 
    scanf("%d", &m);
    if(op<m) {
        tmp.clear();
        rep(i,0,cnt-1) tmp.PB(s[i][0]);
        sort(tmp.begin(), tmp.end());
        int nn=m-op;
        printf("%d\n", nn);
        rep(i,1,nn) printf("%d %d ", tmp[0], tmp[i]);
    }
    else if(op>m) {
        int nn=op-m;
        printf("%d\n", nn);
        rep(ca,1,nn) {
            PII x(n+1, n+1);
            cal();
            rep(i,0,cnt-1) if(s[i].size()>1) {
                PII t(s[i][0], s[i][1]);
                x=min(x, t);
            }
            swap(a[x.first], a[x.second]);
            printf("%d %d ", x.first, x.second);
        }
    }
    else printf("0\n");

    return 0;
}

bzoj 4750: 密码安全

tags：

1、先考虑对每个数求出它作为最大值的区间，即这个数管辖范围的左右边界。单调栈找到左边第一个大于他的位置+1设为l[i]，右边第一个大于等于他的位置-1设为r[i]，答案就是 ans=。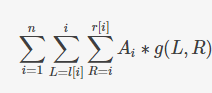

2、分别统计每个数，对于每个二进制位，记录在管辖范围左右0和1的个数，最后和数本身相乘。比如第 i 个数，我们求出这个数二进制所有位数，[l[i],i]里有多少个0和1，与[i,r[i]]里有多少个1和0相乘，再乘上A[i]即可得到这一位下的答案。

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define rep(i,a,b) for (int i=a;i<=b;i++)
#define per(i,b,a) for (int i=b;i>=a;i--)
#define mes(a,b)  memset(a,b,sizeof(a))
#define INF 0x3f3f3f3f
typedef long long ll;
const int N = 200005, mod=1000000061;

int a[N], l[N], r[N], s[N], sta[N], top, n;
void Init()
{
    scanf("%d", &n);
    rep(i,1,n) scanf("%d", &a[i]);
    
    l[1]=1, top=0, sta[++top]=1;
    rep(i,2,n) {
        while(top>0 && a[sta[top]]<=a[i]) top--;
        if(top==0) l[i]=1; else l[i]=sta[top]+1;
        sta[++top]=i;
    }
    r[n]=n, top=0, sta[++top]=n;
    per(i,n-1,1) {
        while(top>0 && a[sta[top]]<a[i]) top--;        //好坑人，<=就挖了 。左闭右开，否则相等的数会重复 
        if(top==0) r[i]=n; else r[i]=sta[top]-1;
        sta[++top]=i;
    }
}
void solve()    // 按位计算 
{
    ll ans=0;
    rep(i,0,31) 
    {
        s[0]=0;
        rep(j,1,n) s[j]=((a[j]>>i)&1)^s[j-1];
        rep(j,1,n) s[j]+=s[j-1];
        rep(j,1,n) {
            ll lw=j-l[j]+1, rw=r[j]-j+1;
            ll l0=s[j-1]-s[max(0,l[j]-2)], r0=s[r[j]]-s[j-1];
            ll l1=lw-l0, r1=rw-r0;            //求出两边 0和 1的数目 
            ll cur=(l0*r1%mod+l1*r0%mod)%mod;
            ans=(ans+ cur*a[j]%mod*((1LL<<i)%mod)%mod)%mod;
        }
    }
    printf("%lld\n", (ans+mod)%mod );
}
int main()
{
    int T;
    scanf("%d", &T);
    while(T--) {
        Init();
        solve();
    } 

    return 0;
}