CF 365(2) C 思维，图形模拟 D 树状数组，离线处理，思维

CF 365(2)

C. Chris and Road

题意：一个人只能竖直走，最大速度为u，要通过宽w的马路。同时一辆车(多边形，蓝色区域)以恒定速度v水平行驶，人不能撞上车，求人通过马路最短时间。

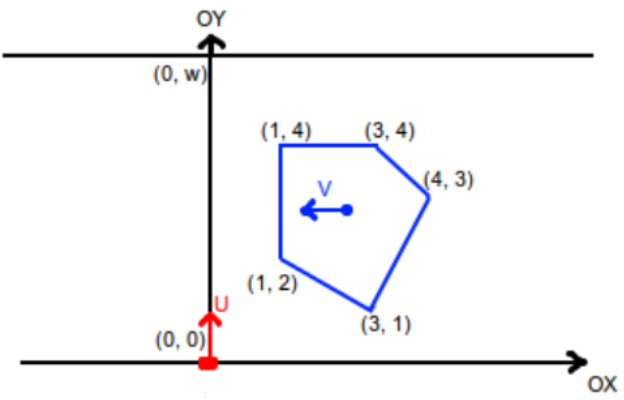
题解：三种情况。(1)人在车过去前通过。(2)人在车过去后通过。(3)人被撞。  一、二种就是以u全速通过，第3种仔细看也不难发现，只要找到对人影响最大的点，人在这个点等车通过，再从这个点全速通过马路。     注：就算感觉自己想不出来，也一定要动笔在草稿纸上分析，说不定就想通了。。

//CF 365(2) C
#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define FF(i,a,b) for (int i=a;i<=b;i++)
#define F(i,b,a)  for (int i=b;i>=a;i--)
#define mes(a,b)  memset(a,b,sizeof(a))
#define INF 0x3f3f3f3f
typedef long long ll;
const int N = 2e5+10;

int n;
double w, v, u, x, y, minn=1e18, maxn=-1e18, ans;
int main()
{
    cin>>n>>w>>v>>u;
    FF(i,1,n) {
        cin>>x>>y;
        double m=x-y/u*v;   //一开始想的是y/u*v/x与1比较，但x或y等于0的情况很尴尬
        minn=min(minn, m);
        maxn=max(maxn, m);
    }
    if(minn>=0) ans=w/u;
    if(maxn<=0) ans=w/u;
    if(minn<0 && maxn>0) ans=w/u+maxn/v;
    cout<<fixed<<setprecision(6)<<ans<<endl;

    return 0;
}

D. Mishka and Interesting sum

题意：给出n个数，m个询问，每次求出第l到第r个数中出现偶数次的数的异或和S0。

题解：设(l,r)内所有数异或和为S1，因所有出现偶数次的数异或和为0，故S1也等于所有出现奇数次的数异或和，所以S0=S1^(区间内出现了的数(不重复)的异或和S2)。想到这里后，只要用一个树状数组维护出S2即可。

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define FF(i,a,b) for (int i=a;i<=b;i++)
#define F(i,b,a)  for (int i=b;i>=a;i--)
#define mes(a,b)  memset(a,b,sizeof(a))
#define INF 0x3f3f3f3f
typedef long long ll;
const int N = 1e6+10;

int n, m, a[N], s[N], f[N], l[N], rr, ans[N];
map<int ,int >M;
vector<int >r[N];
void upd(int x, int v) { for( ; x<N; x+=x&-x) f[x]^=v;  }
int get(int x) { int ret=0; for( ; x>0; x-=x&-x) ret^=f[x]; return ret;  }
int main()
{
    scanf("%d", &n);
    FF(i,1,n) { scanf("%d", &a[i]); s[i]=s[i-1]^a[i]; }
    scanf("%d", &m);
    FF(i,1,m) {
        scanf("%d%d", &l[i], &rr);
        ans[i]=s[rr]^s[l[i]-1];
        r[rr].push_back(i);
    }
    FF(i,1,n) {
        upd(i, a[i]);
        if(M[a[i]]) upd(M[a[i]], a[i]);
        M[a[i]]=i;
        for(auto j:r[i]) ans[j]^= get(n)^get(l[j]-1);   //不是get(i)^get()，是get(n);
    }
    FF(i,1,m) printf("%d\n", ans[i]);

    return 0;
}