一 、背景
2023年9月22日，今天本来开开心心搞测试，奈何雷达有了小情绪，之前能够稳定跟踪但今天不管如何测试对快速运动的行人都无法形成有效的跟踪，本来以为是SDK的问题（近两天测试换了一个新的SDK），换回去之后它也不行了。跟踪跟不上了，看着点云数据还可以，他就是跟不上。算法难搞哦，头疼啊。算了，写写前两天做测试的时候如何解决卡尔曼滤波器发散的问题吧。希望明天雷达歇歇之后能好好工作，文中参考了大佬的一些知识点，如有侵权，请联系删除。
二、关于卡尔曼滤波器发散原因？
2.1、什么是发散
定义：当滤波的实际误差远远超过滤波误差的允许范围，甚至于趋向无穷大，使得滤波器推动作用，这种现象叫做滤波的发散。
2.2、造成卡尔曼滤波发散的原因无外乎以下两点
- 系统的数学模型和噪声的统计模型不准确，这些模型不能反映真实的物理过程，使得观测值与模型不相对应。
- 计算机字长有限，因而存在着计算误差，如舍入误差，这些误差积累起来，降低了滤波精度。严重时，会使计算误差的方差阵逐渐推动正定性，甚至失去对称性，使得增益矩阵的计算值与理论之间的偏差越来越大，因而造成发散。这种发散叫做计算发散。
解决方法：克服由于模型不准确或模型变化所引起的滤波发散问题，可用衰减记忆滤波和限定记忆滤波等方法。当滤波模型不准确时，滤波值中的旧数据比重太大，新数据的比重太小，这是引起发散的重要原因。因此逐渐减小旧数据的权，相对地增加新数据的权（观点1），或者截去旧数据，只保留在观测时刻以前的有限个较新的数据（观点2），这是克服滤波发散的一个有效方法，根据前一观点设计的滤波器这是克服滤波发散的一个有效方法，根据前一观点设计的滤波器叫做衰减记忆滤波器，根据后一观点设计的滤波器叫做限定记忆滤波器。这两种滤波器都是次最优滤波器。
2.3、容易发散的变量
卡尔曼滤波器在工作中，会涉及到下面的序列，这些序列可能会收敛，也可能会发散；
举例：在许多实际问题中，系统噪声方差阵和测量噪声方差阵事先都是不知道的。有时，状态转移矩阵或测量矩阵也不能确切知道。在系统运行过程中，模型还可能不断变化，具体地说，Q,R,A,H不断变化。这些都会引起滤波发散。自适应滤波是在利用测量数据进行滤波的同时，不断地对未知的或不确切知道的系统模型参数和噪声统计特性进行估计或修正，以便改进滤波。因此自适应滤波也是克服滤波发散的重要方法。
由于计算机的舍入误差，使得估计误差协方差P的计算值失去非负定性，甚至失去对称性，因而导致K的计算失真，造成滤波发散现象。平方根滤波方法可用来克服由于计算机舍入误差所引起的滤波发散。
三、利用Kalman处理信号数据总结
其中可调参数有（我觉得新息的地方应该也可以操作，但是实际操作过程中发现影响不大，后面再认真学习一下再说吧）：
P(0)协方差矩阵的初始值；
R 测量噪声
Q 过程噪声
在卡尔曼滤波器实际实现时，测量噪声R一般可以观测得到，是滤波器的已知条件。观测测量噪声协方差R可以通过离线试验获取。
而过程激励噪声协方差Q值比较难以确定，因为我们无法直接观测到过程状态。有时候可以通过Q的手动选择，人为的为过程“注入”一个足够的不确定因素，来产生一个可以接受的结果。
3.1、过程噪声Q对于滤波效果的影响：
Q为对模型（估计）的信任度，Q越大，滤波后的曲线跟测量曲线跟的越紧密，滤波后噪声越大；
Q>1 时，滤波效果差；值越大，效果越差；
Q值越小，滤波效果越明显，太小滤波后效果趋于一条直线；
3.2、P(0)协方差矩阵对于滤波效果的影响
P(0)决定初始增益的大小，影响初始时刻的收敛效果；在整体参数选取合适的时候，初始时刻滤波收敛效果影响不明显。
3.3、测量噪声R对滤波效果的影响
R>0：决定稳态噪声，小了初始增益大，但是稳态容易引入噪声；R越大对噪声越不敏感，即滤波后的数据跳动越小，但R越大， kalman滤波输出收敛的越慢。
随着R值越大，R=50时，滤波收敛效果越明显；R=100；收敛效果特别快；并且滤波效果也趋于一条直线；
整个滤波过程都有延迟，具体影响看不出；需要分析；
Kalman调试本质上是追求系统的收敛和卡尔曼滤波本身收敛过程的平衡点。数学上很难从理论上追求最优解；Q表示对模型（估计）的信任程度，R表示对量测的信任程度，卡尔曼滤波是在模型（估计）和量测之间进行均衡。
四、案例分析
针对上面的知识，给出一个较为好理解的解释（里面一些知识可参考我之前的博客卡尔曼滤波算法：KF、kalman滤波器------数学基础_数据融合_协方差矩阵、卡尔曼滤波器-------卡尔曼滤波公式的详细推导过程）：
不同的人测量硬币的直径，用Zk表示测量的结果，下标k代表第几次测量的结果，由于每个人测量的结果和尺子的误差可能会不一样，例如Z1=50.1mm,Z2=50.5mm,Z3=50.6mm。若要你估计一下真实结果，你可能第一时间会对上面的三个数据直接取平均值。
估计值
随着k的不断增大，1/k不断趋近于0，此时趋近于，可以看出随着k的增加，测量的结果就不重要了。当k比较小的时候，1/k会比较大，测量的结果就非常重要。
五、实际测试
前提：雷达是基于加特兰CAL77S244-AE进行的开发。SDK的版本比较老具体是什么记不太清了。给大家说一下现象。在测试过程中，通常近距离（纵向距离10米左右）跟踪轨迹和点云数据会发生一定的偏移，简单来说就是，跟踪跟不上点云数据了。如下图1所示：图中带箭头的是点云数据，正方形的是跟踪数据，可以明显的看出，二者之间还是有一定差距的。造成这种现象的原因正如前面提到的一样，跟踪更相信模型的结果，而不是更相信量测的结果。通过上面的知识可以知道，若要更相信量测的结果，那么就需要调整R的值，通过调小R的值使它更相信量测的结果。从而更靠近点云数据。图2到图4是通过将R缩小16、64和256倍之后跟踪轨迹和点云数据的情况（本次测试不太严谨，并没有完全控制横向距离相同，后面要是再测试的时候再进行比较吧）。从图中结果来看，随着R的不断减小，导致跟踪的结果更相信测量数据，从而更贴近点云数据。通过这种基本上解决了测试过程中跟踪轨迹偏离的问题（感觉也可以通过提高Q的值来解决这个问题，下次测试的时候再试一下看看吧）。
图1 量测协方差矩阵R不变
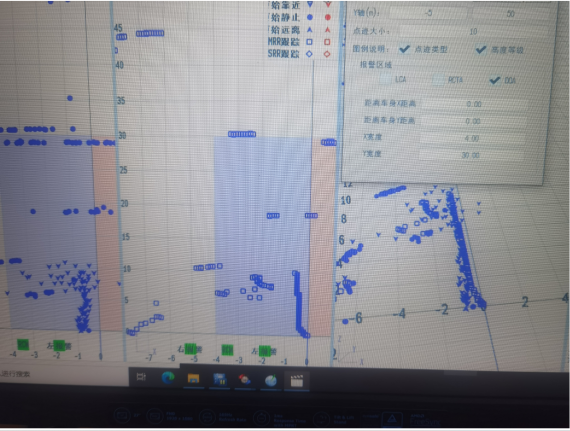
图2 量测协方差矩阵R的十六分之一
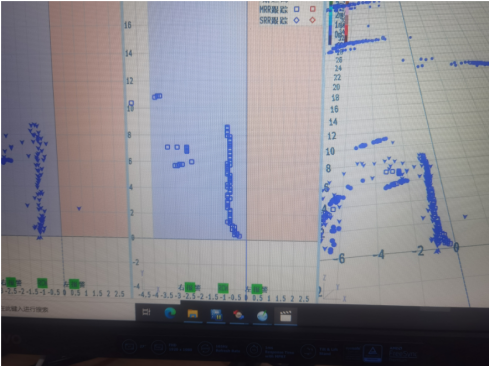图3 量测协方差矩阵R的六十四分之一
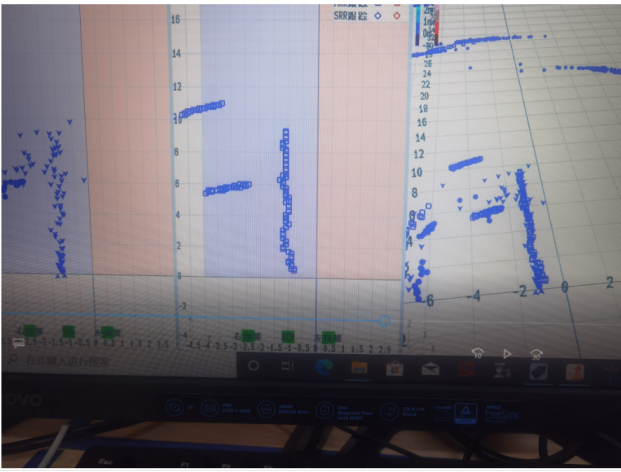
图4 量测协方差矩阵R的二百五十六分之一
六、参考
