一、背景　　

　　这两天看见一个公众号上写的大疆的雷达笔试题。不看不知道，一看吓一跳，基本上快全忘完了，于是赶紧补习补习，我怕到时拿着他的微冲突突我（哈哈）。本文主要是对一些雷达的基础知识进行详细的解析，参考着各位大佬的资料，如有侵权，请联系删除。

二、雷达基础知识

1、FFT主要利用旋转因子的什么性质，减少运算量？

　　答：FFT主要是运用旋转因子的对称性和周期性。

　　1.1、什么是旋转因子：

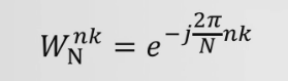
　　W是单位周期复指数序列，n是序列样值的序号，N是DFT变换的长度（N点DFT）

　　表示在复平面的一个单位圆，它的下标N是2π的分母，表示把圆N等分，每一份的角度是2π/N，这个我们叫它基频。

　　旋转因子就是DFT在变换的区间内，等间隔采样序列的频谱函数。

　　说直白点，时域采样是以时间为基本单位隔1s采样一个点。而在频域的采样这个旋转因子就是对应这个间隔。复指数与三角函数的连接是欧拉公式。

　　比如N=4要在频域里采样4个点以什么为采样单位来贯穿这4个点呢？

　　刚好傅里叶变换中有能表达为复指数的，而在复平面这个单位圆里就平均分为N等分，那一份就是频率采样的单位。那一份就是旋转因子的右上角标，如上图4个点的DFT，在频率采样的第一个点就是，第二个点就是，等等。而旋转因子就是表达这个等间隔采样序列的一个频谱函数。

　　1.2、旋转因子的三大性质：

　　其中可约性：下标N和次方nk，同乘以一个数m，旋转因子的值不变。

　　1.3、FFT降低计算量

　　快速傅里叶变换不是一种新的变换，而是离散傅里叶变换的快速算法，而且这个快速算法有很多种，都统称为快速傅里叶变换FFT。

　　如果直接用公式计算DFT，其时间复杂度为O(n*n)，这是难以应用在工程当中的。

　　而基2-FFT的时间复杂度为O(n*log(n))，随着序列的点数增加，其运算效率大大提高（具体推导可以参看参考2和3）。

2、采样率fs，采样M个实数，进行N点（补零为2的整数次幂）FFT变换，其频率分辨率、最大可观测频率是多少？

　　答：实采样（双边谱）的最大可观测频率是采样率的一半(fs/2)，N点FFT的频率分辨率是fs/N。

　　2.1、最大可观测频率

　　Nyquist 采样定理对于具有最大频率 fMAX 的有限带宽信号，等间隔采样频率 fS 必须大于两倍的最大频率 fMAX，才能唯一地重建信号而不会有混叠现象。

　　2.2、频率分辨率

  解释一：

  频率分辨率可以理解为在使用DFT时，在频率轴上的所能得到的最小频率间隔f0=fs/N=1/(N*Ts)=1/T，其中N为采样点数，fs为采样频率，Ts为采样间隔。所以N*Ts就是采样前模拟信号的时间长度T，所以信号长度越长，频率分辨率越好。

　　是不是采样点数越多，频率分辨力提高了呢？其实不是的，因为一段数据拿来就确定了时间T，注意：f0=1/T，而T=N*Ts，增加N必然减小Ts ，因此，增加N时f0是不变的。只有增加点数的同时增加了数据长度T才能使分辨率越好。

　　还有容易搞混的一点，我们在做DFT时，常常在有效数据后面补零达到对频谱做某种改善的目的，我们常常认为这是增加了N，从而使频率分辨率变好了，其实不是这样的，补零并没有增加有效数据的长度，仍然为T。

　　但是补零其实有其好处：

  • 使数据N为2的整次幂，便于使用FFT；
  • 补零后，其实是对DFT结果做了插值，克服“栅栏”效应，使谱外观平滑化。我把“栅栏”效应形象理解为，就像站在栅栏旁边透过栅栏看外面风景，肯定有被栅栏挡住比较多风景，此时就可能漏掉较大频域分量，但是补零以后，相当于你站远了，改变了栅栏密度，风景就看的越来越清楚了（大佬说的很简单易懂）。
  • 由于对时域数据的截短必然造成频谱泄露，因此在频谱中可能出现难以辨认的谱峰，补零在一定程度上能消除这种现象。

　　那么选择DFT时N参数要注意：

  • 由采样定理：fs>=2fh
  • 频率分辨率：f0=fs/N

　　所以一般情况给定了fh和f0时也就限制了N范围：N>=fs/f0。

　　解释二

　　频率分辨率也可以理解为某一个算法（比如功率谱估计方法）将原信号中的两个靠得很近的谱峰依然能保持分开的能力。这是用来比较和检验不同算法性能好坏的指标。

　　在信号系统中我们知道，宽度为N的矩形脉冲，它的频域图形为sinc函数，两个一阶零点之间的宽度为4π/N。

 

 

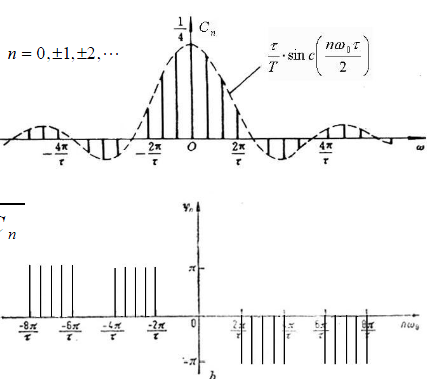
　　由于时域信号的截短相当于时域信号乘了一个矩形窗函数，那么该信号的频域就等同卷积了一个sinc函数，也就是频域受到sinc函数的调制了，根据卷积的性质，因此两个信号圆周频率之差ω0必须大于4π/N。

　　从这里可以知道，如果增加数据点数N，即增加数据长度（注意这里是增加了数据长度），也可以使频率分辨率变好，这一点与第一种解释是一样的。同时，考虑到窗函数截短数据的影响存在，当然窗函数的特性也要考虑，在频率做卷积，如果窗函数的频谱是个冲击函数最好了，那不就是相当于没截断吗？

　　可是那不可能的，我们考虑窗函数主要是以下几点：

  • 主瓣宽度B最小（相当于矩形窗时的4π/N，频域两个过零点间的宽度）；
  • 最大边瓣峰值A最小（这样旁瓣泄露小，一些高频分量损失少了）；
  • 边瓣谱峰渐近衰减速度D最大（同样是减少旁瓣泄露）。

　　在此，总结几种很常用的窗函数的优缺点：

     矩形窗：B=4π/N ，A=-13dB，D=-6dB/oct

     三角窗：B=8π/N ，A=-7dB，D=-12dB/oct

     汉宁窗：B=8π/N ，A=-32dB，D=-18dB/oct

     海明窗：B=8π/N ，A=-43dB，D=-6dB/oct

     布莱克曼窗：B=12π/N，A=-58dB，D=-18dB/oct

　　可以看出，矩形窗有最窄的主瓣，但是旁瓣泄露严重。汉宁窗和海明窗虽主瓣较宽，但是旁瓣泄露少，是常选用的窗函数。

3、实际FFT计算时一般要对数据进行加窗，窗函数的作用是？

答：降低频谱泄露（泄露与窗函数（详细内容请参看参考4））。

　　3.1 泄漏

　　由于信号的非周期截断，导致频谱在整个频带内发生了拖尾现象。这是非常严重的误差，称为泄漏，是数字信号处理所遭遇的最严重误差。但是为什么会出现这种误差呢？原始实际信号为一条单频正弦波，它的频谱怎么会变得如此失真？这个问题很容易解释。这是因为截断后的信号不再是周期信号。

　　对比一下正确的频谱与发生泄漏的频谱，如下图所示，可以看出，泄漏后的频谱的幅值更小，频谱拖尾更严重。当截断后的信号不为周期信号时，就会发生泄漏。而现实世界中，在做FFT分析时，很难保证截断的信号为周期信号，因此，泄漏不可避免。

 

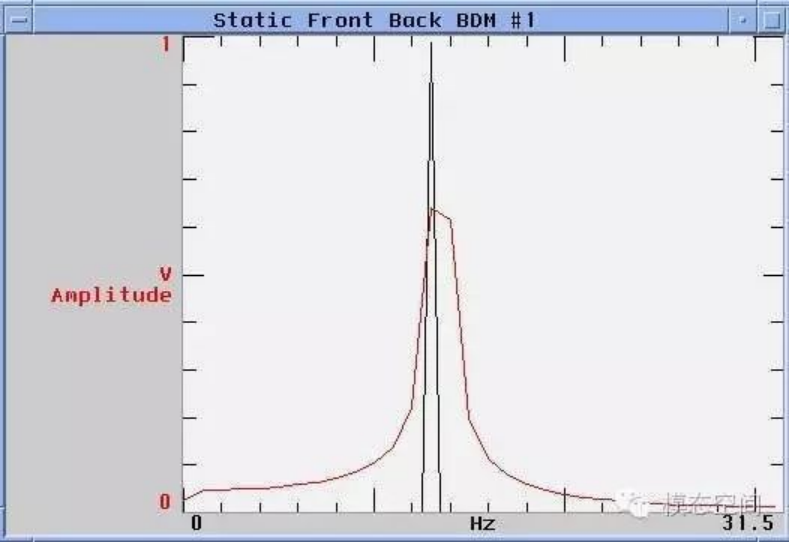
　　现在返回到非周期截断的正弦波，可以看出在截断时间长度内没有捕捉到整数倍个周期正弦波，导致波形发生了失真，似乎在信号周期的末端波形出现了不连续。这就解释了为什么FFT会在整个频带上发生拖尾现象了。本质上，这需要多个傅立叶展开项（多条谱线）去近似这个明显不连续的信号，因此，频谱出现了拖尾现象。

　　3.2 窗函数

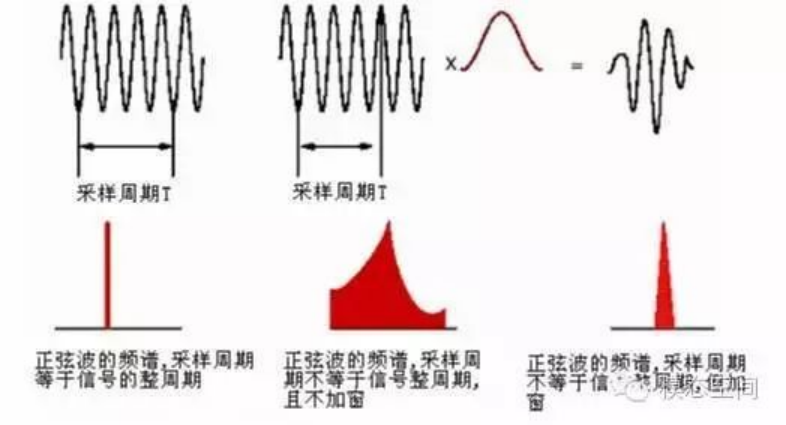
　　为了将这个泄漏误差减小到最小程度（注意我说是的减少，而不是消除），我们需要使用加权函数，也叫窗。加窗主要是为了使信号似乎更好地满足FFT处理的周期性要求，减少泄漏。 

　　如下图所示，若周期截断，则FFT频谱为单一谱线。若为非周期截断，则频谱出现拖尾，如图中部所示，可以看出泄漏很严重。为了减少泄漏，给信号施加一个窗函数（如图中红色曲线所示），原始截断后的信号与这个窗函数相乘之后得到的信号为右侧上面的信号。可以看出，此时，信号的起始时刻和结束时刻幅值都为0，也就是说在这个时间长度内，信号为周期信号，但是只有一个周期。对这个信号做FFT分析，得到的频谱如右侧下边所示。相比较之前未加窗的频谱，可以看出，泄漏已明显改善，但并没有完全消除泄漏。因此，窗函数只能减少泄漏，不能消除泄漏。

 

4、将N次测量回波进行非相干积累，其SNR提高多少倍？

　　答：N次样本的相干（相参）积累将SNR提高了N倍，得到了积累增益。积累的好处不言而喻，高的SNR对信号处理中的检测和参数估计的帮助是十分重要的，但是有得必有失，N个脉冲需要更多的时间，能量和更大的运算代价。

　　对于非相干积累，由于这种积累只利用到了信号的部分信息，也就是幅度信息，所以效率是比相干积累低的。雷达专家Marcum和Swerling指出，非相干积累的增益值在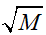和M之间，当M很大时，积累增益接近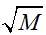。非相干积累的效率要比相干积累低，可以看作是牺牲增益换取的。

三、总结

　　本文详细介绍了雷达基础知识中的旋转因子、频率分辨率、最大可观测频率、窗函数和频谱泄露、补零操作、非相干积累的内容。在大佬们的基础上添加一些自己观点。里面的频率分辨率、窗函数和频谱泄露、补零操作还得好好再琢磨一下。希望能够对大家有所帮助。

四、参考

　　1、频率分辨率的两种解释，这回终于彻底明白了！（声振之家）

　　2、数字信号处理——快速傅里叶变换（队长-leader）

　　3、DFT中的旋转因子W的理解（迷失在频域中）

　　4、什么是泄漏？ (模态空间)

　　5、往年 | 大疆雷达算法校招笔试题目解析（调皮连续波）