这周深圳台风，对于一个河南人来说，第一次碰见台风，心中有一些激动，那个脑中的画面，狂风卷积着乌云，大雨磅礴，电闪雷鸣。结果到最后感觉也没啥啊，还没有老家当时刮风大。难道我遇见了一个假台风？题外话到这，咱们回到正题，今天这篇是高斯白噪声下雷达测量精度的最后一篇--------角度精度公式的详细推导。
一、角度的估计精度
天线扫描时角度的估计精度问题，与时延估计类似。时延估计中输入波形s(t)与频谱S(w)成傅里叶变换对关系。而天线方向图函数F(θ)与其口径电流分布f(x)也有相对应的傅里叶变换关系。
图1给出了某平面天线在x轴的孔径为a，口径电流分布函数为f(x)，根据天线理论，电压方向图F(θ)为：
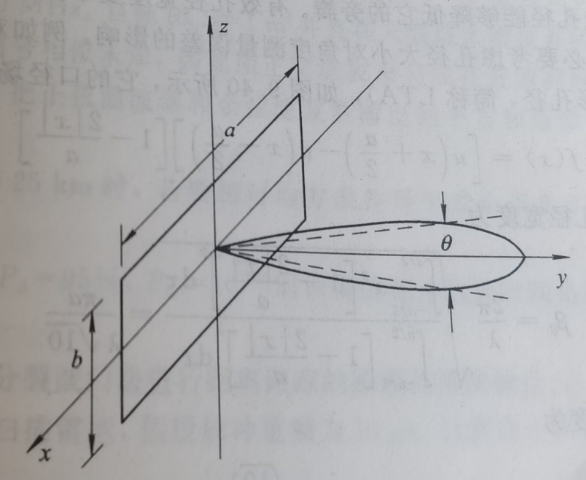
图1 平面天线及其方向图
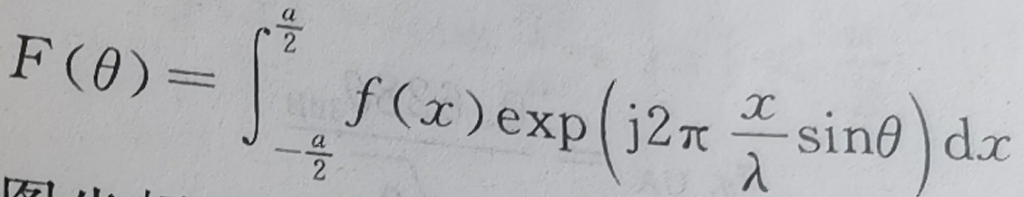
当θ足够小时，sinθ约等于θ，方向图坐标对波长λ归一化后得到公式：
可以看出F(θ/λ)是f(x)的反傅里叶变换。这与波形和它的频谱之间的关系类似。具体可参考前面关于距离和速度精度的公式推导。因此类比可得到测角误差为：
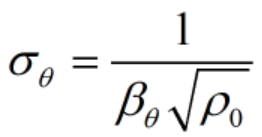
其中λ为波长，βθ为天线的均方根孔径宽度，并且：
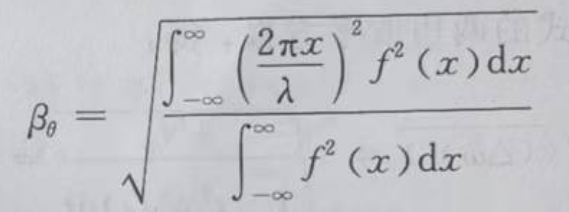
二、两个例子
1、矩形孔径(UA)
对于孔径具有均匀幅度照射的天线来说，它的有效孔径带宽为：
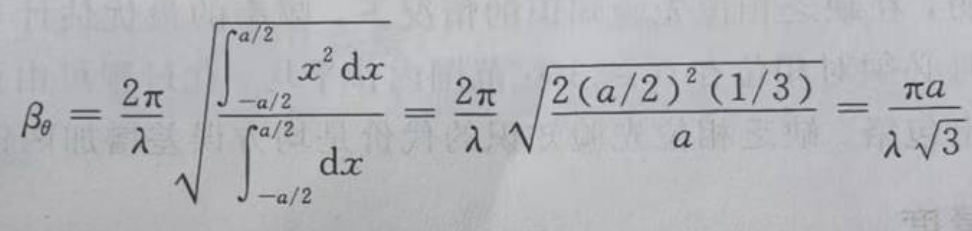
因此，它对应的测角误差为：
又因为半功率波束宽度θ3dB与a和λ的关系为：θ3dB=0.88λ/a；所以测角的均方根误差为：
可以看出测角精度与θ3dB成正比，与√ρ0成反比。例如当θ3dB=3°，信噪比ρ0=20dB，则测角精度为0.6053°。约为波束宽度的1/20。
2、线性锥形孔径(LTA)
已知尖锐的天线孔径能够降低它的旁瓣。有效孔径宽度变小使得旁瓣降低，但是同时主波束变宽。因此有必要考虑孔径大小对角度测量误差的影响。例如线性锥形孔径。如图2所示，它的口径场分布函数为：
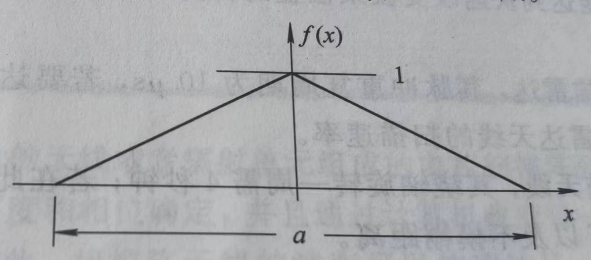
图2 线性锥形孔径图
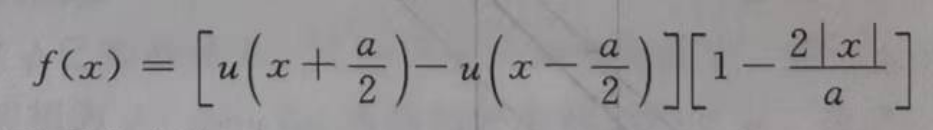
因此天线的均方根孔径宽度为 ：
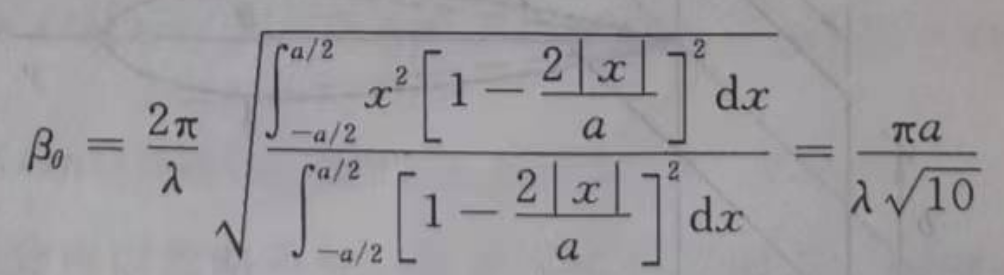
则LTA天线的测角精度为：
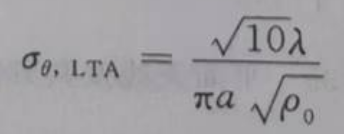
对比UA和LTA的测角精度可知：
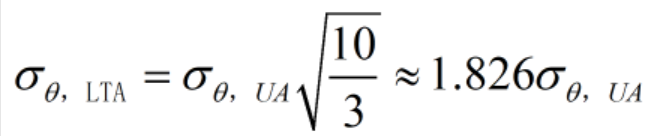
上式结果表明相同信噪比条件下，线性锥形孔径由噪声引起的角度测量精度约为矩形孔径的两倍。因此，对于尺寸为a的孔径下的余弦照射f(x)=cos(pi*x/a)(其中|x|<=a/2)，有效孔径带宽为1.33a/λ;而对抛物面照射有效孔径带宽为0.93a/λ。
三、总结
到这高斯白噪声条件下的测量精度就全部结束了，其中测距精度由信号的有效带宽和信噪比决定，测速精度主要由信号的有效时宽和信噪比来决定，测角精度主要由天线孔径和信噪比决定。不难看出，在三个测量精度中信噪比都会对其产生影响，左右测量的精度。因此如果雷达在测量过程中点云数据的精度不高，可以适当的调节一下信噪比来提高雷达的测量精度。
关于雷达测量精度的所有内容到这就结束了，后面应该会针对雷达的波形复用和分离进行好好学习，主要包括FDMA\TDMA\DDMA\CDMA。大家如果感兴趣的话不妨后面看一看。
四、参考文献
《现代雷达系统分析和设计》
