今天来到了深圳市图书馆，有一说一座位挺多的，地方也挺大的，可能是时间比较长了。没有光明区的图书馆特别让人惊艳。而且连WIFI还需要读者证号，有一点不方便。回到正题，承接上回，上一篇学习了高斯白噪声下雷达距离精度公式详细推导，给出了详细的推导过程。接下来我们接着来学习高斯白噪声下雷达速度精度公式详细推导。话不多说直接开始。
与距离精度推导公式一样，速度精度公式的推导过程中也需要用到一个公式，里面的具体参数意义可以参考之前的文章高斯白噪声下雷达测量精度---------距离精度公式详细推导，这里就不过多的解释了：
一、频率的估计精度
单基地雷达中的速度的测量等效于多普勒频移的测量。频率估计的另一个应用是在调频连续波雷达中，用瞬时频率来测量距离。
频率ω包含在中频信号中，参考信号为：
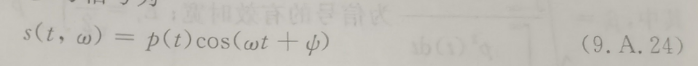
p(t)的持续时间为T，T远大于2Π/ω。
将公式9.A.24带入9.A.11d中，对频率的估计为ωest，
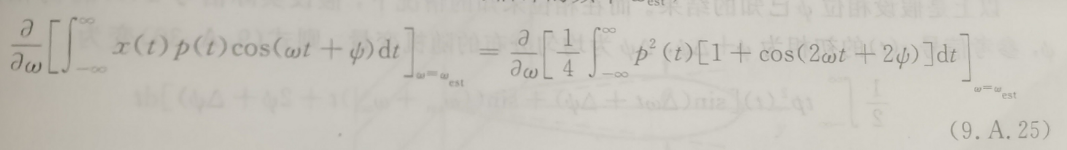
当T远大于2Π/ω时，上式右边的第二项积分可近似为0，而第一项由于和ω无关，则右侧公式的结果为0。然后对左侧的公式进行微分化简。那么上式可以得到：
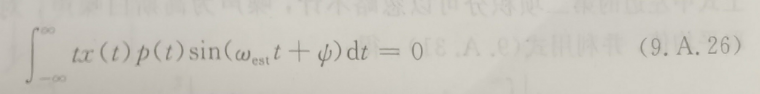
或者将三角函数展开，再用Us和Uc来表示。将其简化为：
其中
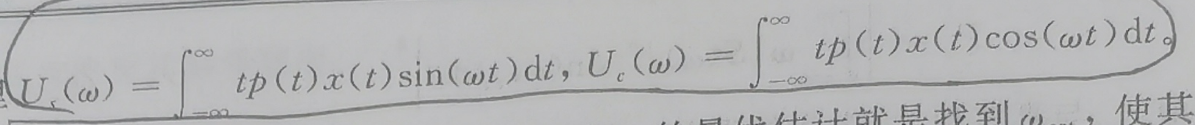
1、相位已知：
给定相位Ψ，根据公式9.A.27,频率ω的最优估计就是找到ωest让其满足：
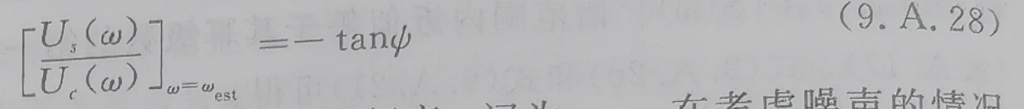
假如9.A.24为实际信号，ω为实际信号频率，记为ωact。考虑噪声的情况下，观测信号为：
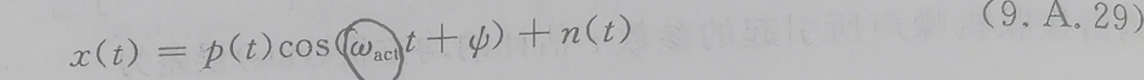
书上写得是将9.A.29带入9.A.11d中，但个人觉得应该是带入9.A.26中。将得到的噪声结果移动到等式右侧中。
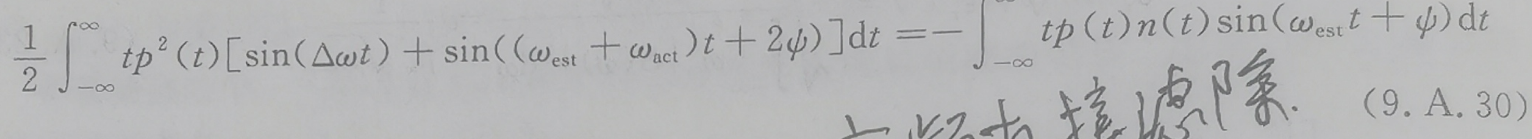
其中Δω=ωest-ωact为频率估计误差。
当T远大于2Π/ω时，ω=ωest或者ω=ωact,上面公式中的左边第二项积分可以忽略（高频分量可以滤除），然后对两边求绝对值的平方，再求平均得到：
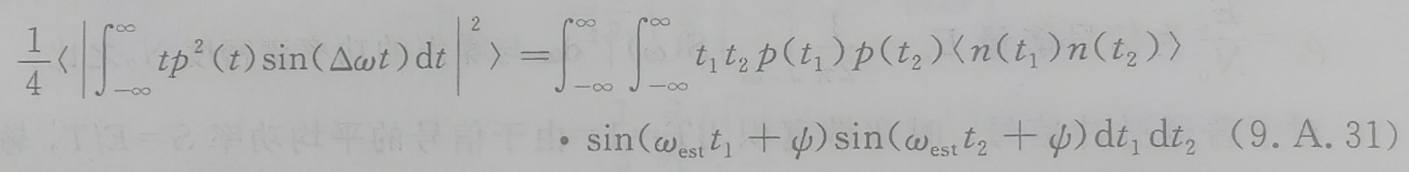
假设为高斯白噪声；那么
N0为噪声功率密度，Δω足够小，sin(Δωt)可以用幂级数的第一项Δωt来代替。因此可以化简为（这个右侧的两倍是sin2(x)的积分的结果）：
对上面的等式取平方根处理并移项，频率ω估计的均方根误差为：
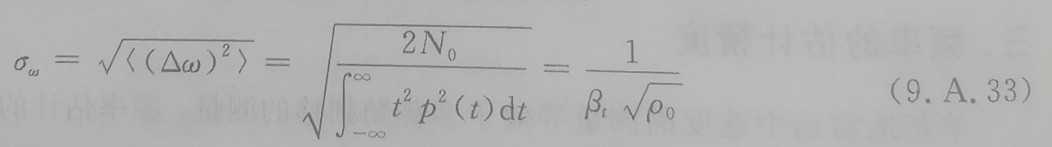
2、相位未知：
在相位未知的情况下，假设实际信号x(t)的初相为Ψ，参考信号s(t)的初相为Ψ+ΔΨ，ΔΨ为均匀分布的随机变量。那么公式9.A.30就变成了：
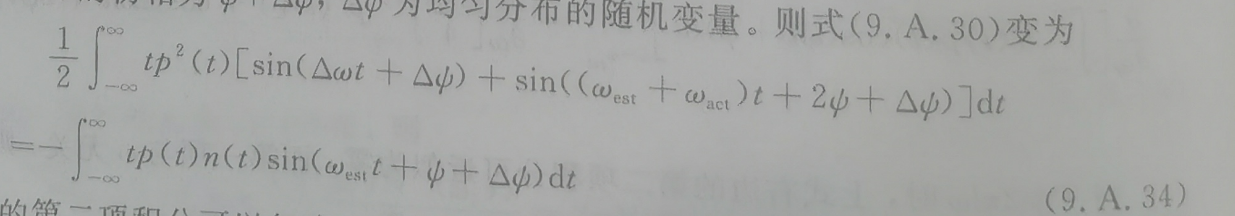
同样上式左侧的第二项可以忽略不记，噪声为高斯白噪声，对两边取绝对值的平方，再取平均值并利用9.A.31，可以得到
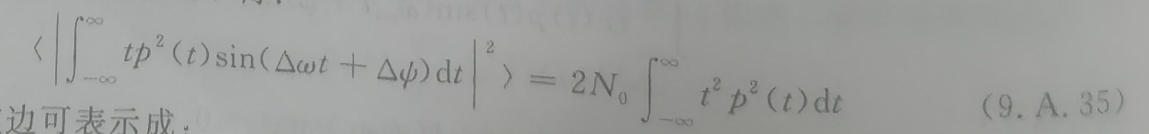
上式左边可以表示为
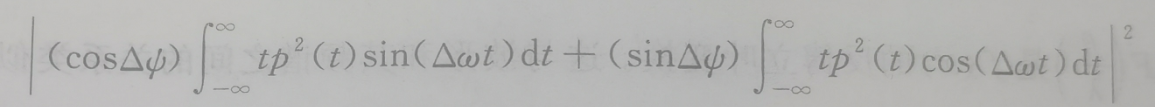
其中p2(t)由于是偶函数，上式中的第二项为为奇函数（f(x)=-f(-x)）,所以为0.假设Δω、ΔΨ相互独立，并且Δω足够小。那么sin(Δωt)≈Δωt。上式可以化简为：
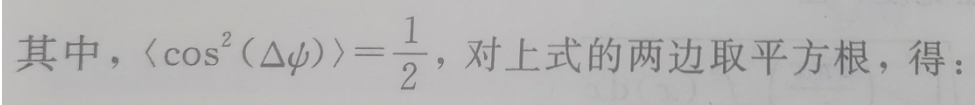
书上给的答案是未知相位的精度误差是已知相位精度误差的2倍，但从公式结果来看应该是√2倍才对。
二、总结
从上面的结果来看，在缺乏相位先验知识的情况下，频率的最优估计与相位有关。这也就是说在频率估计时必须对相位在0°和360°范围内作平均，此过程可由正交滤波完成并得到匹配滤波器的输出包络。缺乏相位先验知识的代价是均方误差增加√2倍。
关于高斯白噪声条件下速度精度的公式推导到这里就结束了，里面有很多三角函数积分、微分的知识，过程本身并不难。就是有些数学知识需要大家再重温掌握一下。文章就到这里了，感兴趣的可以点个关注，后面还有角度精度的公式推导。
三、参考文献
《现代雷达系统分析和设计》
