一、背景
前面写的一篇博客毫米波雷达入门知识里面介绍了距离精度、速度精度和角度精度。并给出了一个简单公式来说明哪些因素影响它们的大小。但具体怎么得到的并未说明，正好前两天在《现代雷达系统分析和设计》这本书上有看见相关内容，就趁着周末，再加上光明区的这个图书馆这么给力的，记录一下，加深自己的印象，也希望能够帮助到大家，话不多说咱们进入主题。
首先，本文是在高斯白噪声条件下的最大似然法的测量精度，主要包括三个部分分别是时延的估计精度、频率的估计精度和角度的估计精度，本文就先对时延（距离）的估计精度进行详细推导，后面会对频率（速度）和角度的估计进行详细推到。其中的最大似然估计方法不做过多的描述，只把要用到的公式单独拎出来，大家如果想详细了解的话可以去参看《现代雷达系统分析和设计》中的相关内容。另外如有侵权请留言删除。
二、噪声背景下的最佳估计
参数估计是通过观测数据来构造相应函数。该函数应能利用这一组观测数据的信息，以便由它获得参量的最佳估计。参数估计的方法有很多。其中不乏由代价最小的贝叶斯估计、最大后验估计、最大似然估计等。由于雷达本身的性质，无法知道代价函数和参量的先验知识，因此通常使用最大似然估计方法。下面简要介绍一下高斯背景下最大似然估计的测量精度。由于后面的距离、速度和角度精度测量都要用到这个公式。因此在这直接给出，用于后面的推导，具体怎么得到的不做过多介绍。
公式中x(t)为接收输入端的波形，它是信号加噪声n(t),即x(t)=s(t;β)+n(t)。其中参数β就是待测量的（可以是速度、距离、角度或者径向速度），所以测量之前它是未知的。另外运用最大似然估计对参数β进行的估计表示为βest。
另外由于一般情况下β是多维的，包含一组参数，因此将参数矢量表示为：
β=[β1 β2 ...... βM]T
因此可以利用公式9.A.11d对雷达坐标（参数β分别为角度θ、时延τ和多普勒频率fd）进行估计和推导其测量精度。
三、时延的估计精度
下面针对时延参数为例进行讨论。由于雷达角度上的分辨率主要是天线方向图决定。而距离和多普勒分辨能力取决于雷达的信号形式和相应的信号处理方法，因此，假设期望信号接收到的中频脉冲信号为
其中sexp(t-τ)为期望信号，α为信号幅度，ψ为期望信号的初始相位，τ为时延。
单基地雷达中，一般通过估计脉冲到达时间来实现对距离的估计。此时，公式9.A.11d中需要估计的参数β定义 为τ。信号这时为s(t-τ)。此时结合9.A.11d得到公式9.A.14。（公式之所以等于零，这点我也还没想清楚。后面如果理解了再更新，如果大家知道为什么等于零欢迎留言探讨学习一下）
对上式中的x(t)和s(t-τ)进行傅里叶变换得：
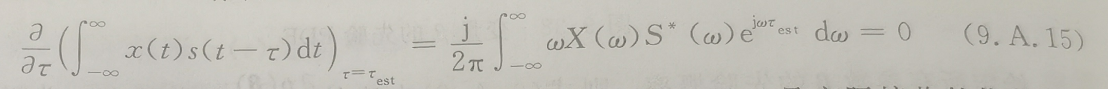
公式中S*(ω)为S(ω)的共轭，S(ω)是期望信号的傅里叶变换，X(ω)是实际接收的信号加噪声的傅里叶变换。
这里τact是实际到达时间，N(ω)是噪声的傅里叶变化的结果。将9.A.15和9.A.16相结合得到：
这里的Δτ其实是τact和τest之间的误差，对上式双边取绝对值平方求平均，那么等式左侧是信号功率，右侧是噪声平均功率。在时间T内，上式中的噪声平均功率为：
在信号频带内，噪声谱近似均匀分布，那么：
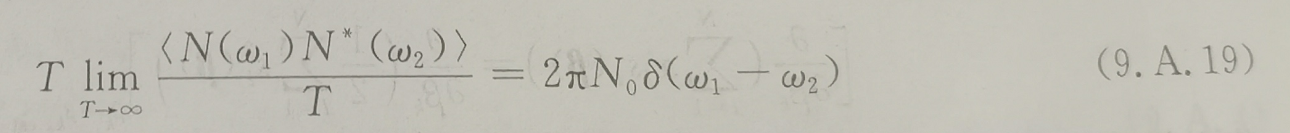
N0为噪声的功率谱密度（单位为W/Hz，即单位带宽上的功率）因此噪声功率可化为：
同样对公式左边取模平方得到信号功率为：
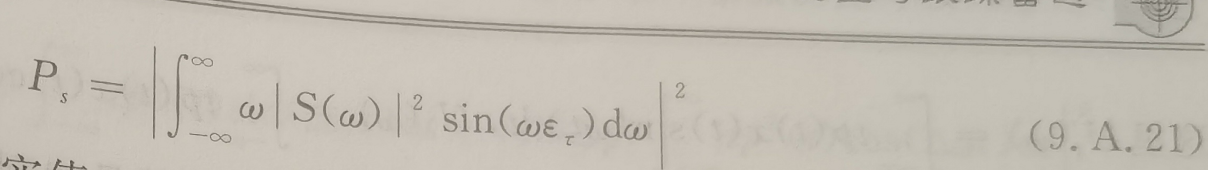
其中ετ表示估计值τest和真实值τact之间的误差，即ετ=τest-τact。如果估计误差ετ足够下，那么sin(ωετ)在|S(ω)|2谱范围内近似等于幂级数的第一项，sin(ωετ)约等于ωετ。那么结合17、20和21可得：
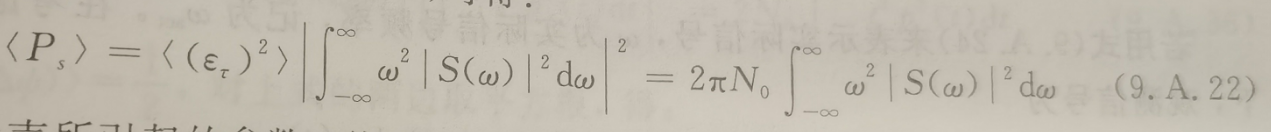
则由接收机噪声所引起的参数时延τ估计的均方跟误差为：
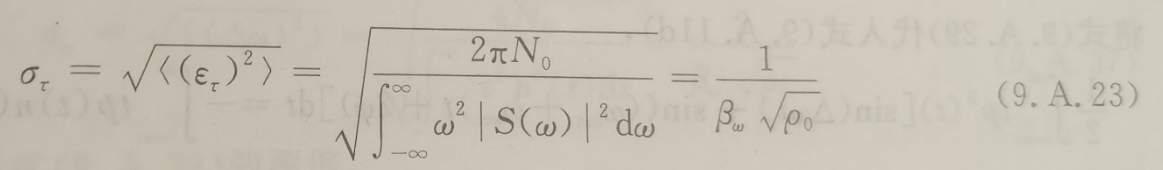
其中：
为信号有效带宽（单位为弧度/秒）；ρ0为信号能量与噪声的功率谱密度N0之比。信号能量可表示为：
对于普通脉冲信号，时宽带宽积BT=1，由于信号的平均功率S=E/T，输入噪声的平均功率N=N0B，那么：
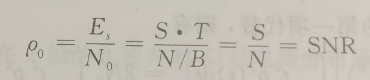
因此，ρ0也就是匹配滤波器的输出信噪比。
以上就是高斯白噪声下雷达的距离精度公式的详细推导，理解起来应该不难，里面主要用到的知识有傅里叶变换和微积分的原理，另外个人觉得里面最核心的两个东西就是噪声功率和信号功率。如果搞懂这点基本上就没太大问题了。后面会更新一下速度和角度精度公式的详细推导，如果大家感兴趣的话不妨点赞关注收藏一下，方便以后找。
四、参考文献：
《现代雷达系统分析和设计》
