参考内容：书籍《卡尔曼滤波原理及应用------matlab仿真》这本书对kalman算法的解析很清晰，MATLAB程序很全，适合初学者（如有侵权，请联系删除(qq:1491967912)）
1、EKF算法存在的问题
上一篇学习的EKF算法对非线性的系统方程或者观测方程及进行泰勒展开并保留其一阶项，由于仅保留了一阶项，将引入一些线性误差。另外当线性化假设不成立时，该方法会造成跟踪性能下降，最终可能导致跟踪发散。除此之外，通常计算系统的状态方程和观测方程的雅可比矩阵是一个很复杂的问题，这样会增加算法的复杂度。不利于实际的应用。
2、无迹kalman滤波相对于扩展kalman滤波的优点
无迹kalman滤波（UKF）不是采用的将非线性函数线性化的做法。无迹kalman仍然采用的是线性kalman滤波的架构，对于一步预测方程，使用无迹变换（UT）来处理均值和协方差的非线性传递问题。UKF算法是对非线性函数的概率密度分布进行近似，用一系列确定样本来逼近状态的后验概率密度，而不是对非线性函数进行近似，不需要对雅可比矩阵进行求导。UKF没有高阶项忽略，因此对于非线性分布的统计量有较高的精度，有效克服了扩展Kalman滤波的估计精度低、稳定性差的缺陷。
3、无迹变换（UT变换）
UT变换其实现原理是在原来分布中按照某个规则去取点，使这些点的均值和协方差状态分布与原状态分布的均值和协方差相等；将这些点带入非线性函数中，相应的得到非线性函数的点集，通过这些点集可求取变换的均值和协方差。这种得到的非线性变换后的均值和协方差精度最少具有2阶精度；对任何一种非线性系统，当高斯型状态微量经由非线性系统进行传递，利用这组取样点获得精确到三阶矩的后验均值和协方差。
4、无迹Kalman滤波原理
4.1 无迹变换
无迹kalman滤波也是一种非线性滤波方法。与扩展kalman不同的是，无迹Kalman不对非线性方程f和h在估计点处做线性逼近，而是利用无迹变换（UT变换）在估计点的周围确定采样点，用这些样本点表示的高斯密度近似状态的概率密度函数。
非线性变换比较如下图所示
图中Px为相对应的过程噪声方差，从结果来看UKF算法在效果上与EKF相比更加准确。
4.2 UT变换基本原理举例。
假设有一个非线性变换y=f(x)。状态向量x为n维随机变量，并且已知其均值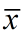
和方差P，可通过下面的UT变换来得到2n+1个Sigma点X和相应的权值w来计算y的统计特征：
（1）计算2n+1个Sigma点，即采样点，这里的n指的是状态的维数
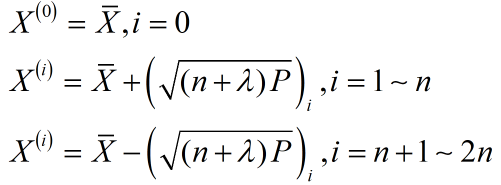
上式中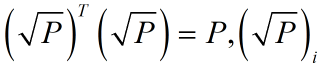
表示矩阵方根的第i列。
（2）计算采样点的相应权值
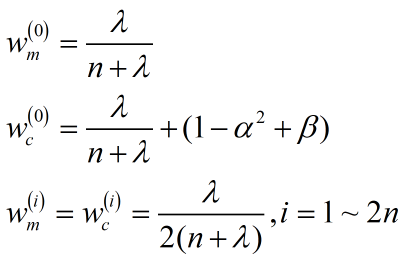式中下标m为均值 ，c为协方差，上标为第几个采样点。参数
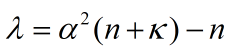是一个缩放比例参数，用来降低预测的误差，α的控制采样点的分布状态，
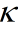为待选参数，其具体取值虽然没有界限，但通常应保证
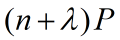为半正定矩阵待选参数
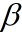是一个非负的权系数可以合并方程中的动差，这样可将高阶项的误差包含在内。
UT变换得到的sigma点集具有以下性质。
（1）由于sigma点集围绕均值对称分布并且对称点具有相同的权值，因此sigma集合的样本均值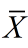
，与随机变量X的均值相同。
（2）对于sigma点集的样本方差与随机变量X的方差相同。
（3）任意正态分布的sigma点集，是由标准正太分布的sigma集合经过一个变换得到的。
补充：正定矩阵和半正定矩阵
给定一个大小为N*N的实对称矩阵A，若对于任意长度为N的非零向量X。有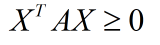
恒成立，则矩阵 A是半正定矩阵（
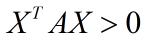恒成立，则矩阵 A是正定矩阵）。
5、无迹kalman滤波算法的实现
对于不同时刻k，由具有高斯白噪声W（k）的随机变量X和具有高斯白噪声V(k)的观测变量Z构成的非线性系统可写成下面的格式。
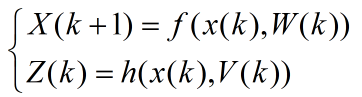
式中，f是非线性状态方程函数；h是非线性观测方程函数。假定W（k）具有协方差矩阵Q，V(k)具有协方差矩阵R。随机变量X在不同时刻k的无迹kalman滤波算法的基本步骤如下所示。
第一步：根据4.2节求采样点和采样点对应的权值的公式获取一组采样点（sigma点集）及其对应的权值。
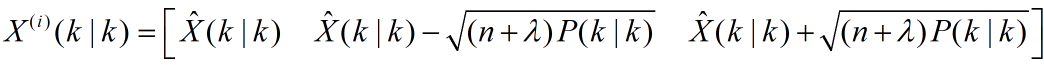
第二步：计算2n+1个sigma点集的一步预测，i=1,2,...,2n+1.
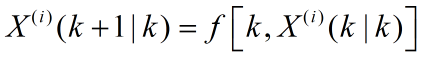第三步：计算系统状态量的一步预测及协方差矩阵，它由sigma点集的预测值加权求和得到，其中权值
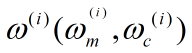通过4.2节权值计算公式得到的。
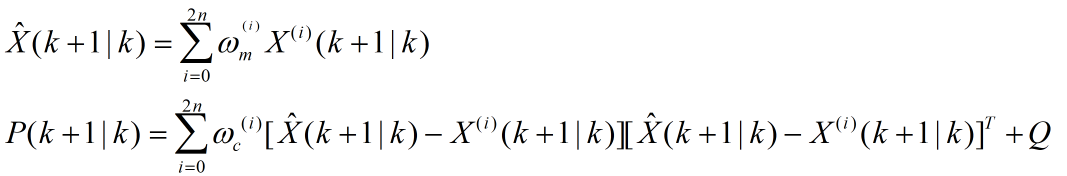
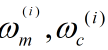分别为均值权重和协方差权重。
这是UKF不同于传统的kalman滤波算法的主要点，传统的kalman算法只需通过上一时刻的状态代入状态方程，仅计算依次便获得状态的预测；但UKF在此利用一组sigma点的预测的基础上，并计算对它们加权求均值，得到系统状态量的一步预测。
第四步：根据系统状态量的一步预测值，再次使用UT变换，产生新的sigma点集。
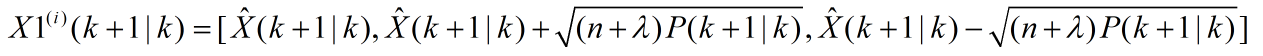
第五步：将由步骤4预测的sigma点集带入预测方程，得到预测的观测量，i=1,2,...,2n+1.
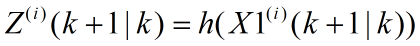
第六步：由步骤5得到sigma点集的观测预测值，通过加权求和得到系统预测的均值和协方差。
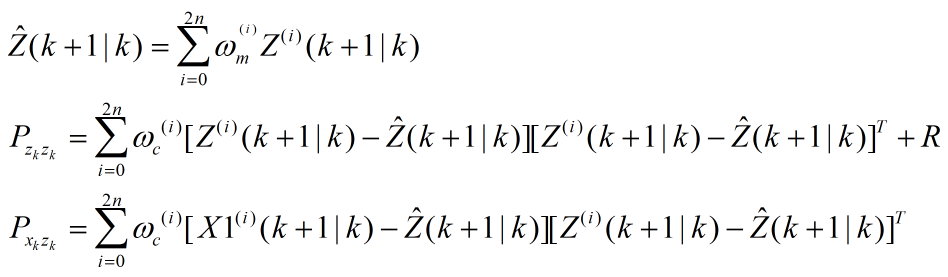
第七步：计算kalman增益矩阵
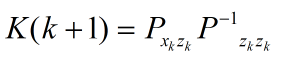
第八步：最后计算系统的状态更新和协方差更新。
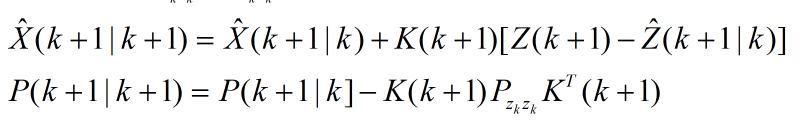
总的从上面可以看出，无迹kalman滤波在处理非线性滤波时并不需要在估计点处做泰勒级数展开，然后再进行前n阶近似，而是在估计点附近进行UT变换，使获得的sigma点集的均值和协方差与原统计特性匹配，再直接对这些sigma点集进行非线性映射，以近似得到状态概率密度函数。这种近似其实质是一种统计近似而非解。
6、无迹kalman滤波在目标跟踪中的应用
6.1原理介绍
假定目标做匀速直线运动，在单个观测站对目标进行观测的前提下，再假设目标的初始状态已知。目标的运动方程可以写成如下形式。
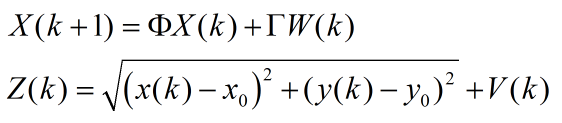
式中：
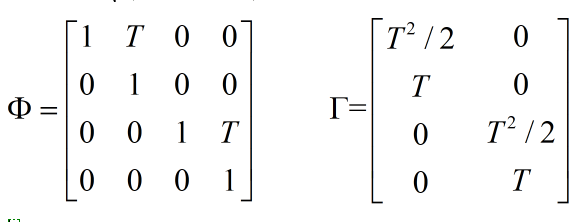
W(k)的均方差为Q=σw*diag([1,1]),σw<<1为一个可调节的参数。下面是基于UKF算法的跟踪matlab程序。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 无迹kalman滤波在目标跟踪中的应用
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
close all
T=1; %雷达扫描周期
N=60/T; %总的扫描次数
X=zeros(4,N); %目标x，vx，y，vy
X(:,1)=[-100 2 200 20]; %目标的位置和速度初始化
Z=zeros(1,N); %目标的观测位置信息
delta_a=1e-1; %该值是一个可调节的参数，需要起值<<1,若增大该值，轨迹会变成曲线
Q=delta_a*diag([0.5 1]); %过程噪声均方值
G=[T^2/2 0;T 0;0 T^2/2;0 T]; %过程噪声驱动矩阵
F=[1 T 0 0;0 1 0 0;0 0 1 T;0 0 0 1]; %状态转移矩阵
Xstation=[200 300]; %雷达站的位置
R=5; %观测噪声方差
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
v=sqrtm(R)*randn(1,N); %观测噪声矩阵
w=sqrtm(Q)*randn(2,N); %状态噪声矩阵（其实是加速度）
for t=2:N
X(:,t)=F*X(:,t-1)+G*w(:,t-1); %目标真实轨迹
end
for t=1:N
Z(t)=Dist(X(:,t),Xstation)+v(:,t); %目标观测轨迹
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
L=4; %状态维数
alpha=1; %控制采样点的分布状态
kalpha=1;
belta=2; %不小于0的权系数
lamda=-3;
%lamda=alpha^2*(L-kalpha)-L; %缩放比例参数，用来降低总的预测误差
%%%%%%%%%%%%%%%%%%%%求取采样点相应的权值%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for j=2:2*L+1
% Wm(j)=lamda/(2*(L+lamda));
% Wc(j)=lamda/(2*(L+lamda));
Wm(j)=1/(2*(L+lamda));
Wc(j)=1/(2*(L+lamda));
end
Wm(1)=lamda/(L+lamda);
Wc(1)=lamda/(L+lamda)+(1-alpha^2+belta);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
X_ukf=zeros(4,N);
X_ukf(:,1)=X(:,1); %UKF初始化
P=eye(4); %协方差矩阵初始化
for i=2:N
X_estimate=X_ukf(:,i-1);
%第一步：获得一组sigma点集
cho=(chol(P*(L+lamda)))'; %chol的作用相当于sqrtm函数
for k=1:L
xgamaP1(:,k)=X_estimate+cho(:,k);
xgamaP2(:,k)=X_estimate-cho(:,k);
end
xSigma=[X_estimate,xgamaP1,xgamaP2]; %sigma点集
%第二步：对sigma点集进一步预测
xSigma_pre=F*xSigma;
%第三步：利用第二步的结果计算均值和协方差
X_pred=zeros(4,1); %均值
for k=1:2*L+1
X_pred=X_pred+Wm(k)*xSigma_pre(:,k);
end
P_pred=zeros(4,4); %协方差矩阵预测、
for k=1:2*L+1
P_pred=P_pred+Wc(k)*(X_pred-xSigma_pre(:,k))*(X_pred-xSigma_pre(:,k))';
end
P_pred=P_pred+G*Q*G';
%P_pred=P_pred+G*Q*Q'*G';
%第四步：根据预测值，再一次使用UT变换，得到新的sigma点集
cho_new=(chol(P_pred*(L+lamda)))';
for k=1:L
XaugsigmaP1(:,k)=X_pred+cho_new(:,k);
XaugsigmaP2(:,k)=X_pred-cho_new(:,k);
end
Xaugsigma=[X_pred XaugsigmaP1 XaugsigmaP2];
%第五步：观测预测
for k=1:2*L+1 %观测预测
Zsigmapre(1,k)=hfun1(Xaugsigma(:,k),Xstation);
end
%第六步：计算观测预测均值和协方差
Zpred=0; %观测预测的均值
for k=1:2*L+1
Zpred=Zpred+Wm(k)*Zsigmapre(1,k);
end
Pzz=0; %协方差矩阵
for k=1:2*L+1
Pzz=Pzz+Wc(k)*(Zsigmapre(1,k)-Zpred)*(Zsigmapre(1,k)-Zpred)';
end
Pzz=Pzz+R;
Pxz=zeros(4,1);
for k=1:2*L+1
Pxz=Pxz+Wc(k)*(xSigma_pre(:,k)-X_pred)*(Zsigmapre(1,k)-Zpred)';
end
%第七步：计算kalman增益
K=Pxz*inv(Pzz); %kalman增益
%第八步：状态和协方差更新
X_estimate=X_pred+K*(Z(i)-Zpred); %状态更新
P=P_pred-K*Pzz*K'; %协方差更新
P0=P;
X_ukf(:,i)=X_estimate;
end
%误差分析
for i=1:N
Err_kalmanFilter(i)=Dist(X(:,i),X_ukf(:,i)); %滤波后的误差
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%画图
figure;
hold on;box on;
plot(X(1,:),X(3,:),'-k.'); %真实轨迹
plot(X_ukf(1,:),X_ukf(3,:),'-r+'); %无迹kalman滤波轨迹
legend('真实轨迹','UKF轨迹')
figure
hold on;box on
plot(Err_kalmanFilter,'-ks','MarkerFace','r');
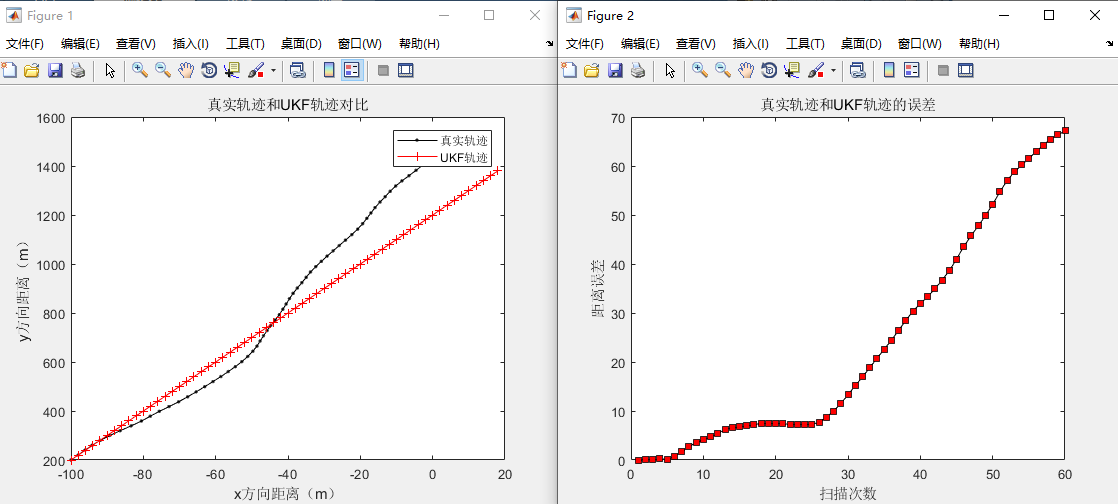
这是针对匀速运动的目标进行跟踪的应用，但在实际情况中，往往目标运动速度是变的，需要考虑加速度信息，下一期UKF算法会针对匀加速的目标跟踪进行学习，这时状态矩阵和量测矩阵从匀速运动的四维变成了匀加速的六维矩阵。具体步骤敬请期待。
