参考内容：书籍《卡尔曼滤波原理及应用------matlab仿真》这本书对kalman算法的解析很清晰，MATLAB程序很全，适合初学者（如有侵权，请联系删除(qq:1491967912)）

本文内容从两个方面来学习EKF在目标跟踪中的应用。

　　1、数学建模

　　2、基于观测距离的EKF目标跟踪算法

1、数学建模。

　　以匀速直线运动系统为例，介绍目标跟踪的状态方程和观测方程的建立过程，也即数学建模过程。

　　假定目标做的是匀速直线运动，速度为v，目标在k时刻的位置设为state（k）,经过采样时间T，目标的位置信息为

state(k+1)=state(k)+v*T.显然在直角坐标系中目标有x和y两个方向的分量，运动系统的状态量有x方向上的位置、y方向上的位置、x方向上的速度和y方向上的速度四个量。运动过程中还存在随机扰动u(k)的干扰（其实是加速度带来的影响，由于前提是匀速直线运动，所以把加速度当成了随机扰动）因此系统可以表示为：

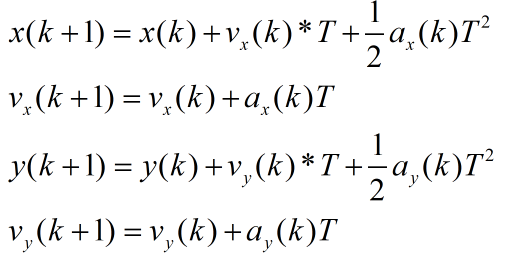
　　令 

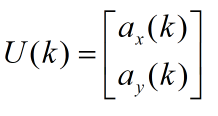
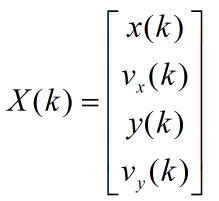
　　系统的状态方程可以化简为：

 

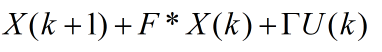
　　式中的

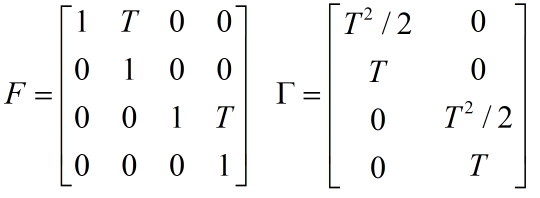
       接下来是观测方程：以雷达为例，假定雷达的位置为（x0,y0）,目标k时刻的位置为（x(k),y(k)）,测得的目标和雷达之间的距离为Z，则观测方程可写为。

 

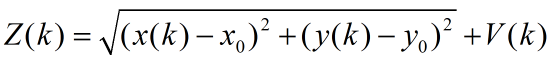
 　　其中，V（k）称为测量噪声，是雷达自身测量的误差，其方差为R。从上述模型来看，状态方程是线性的，但观测方程是非线性的。

2、基于观测距离的EKF目标跟踪算法

　　假定目标做匀速直线运动，初始状态X（0）已经通过航迹起始算法获得。过程噪声u(k)可以写为：

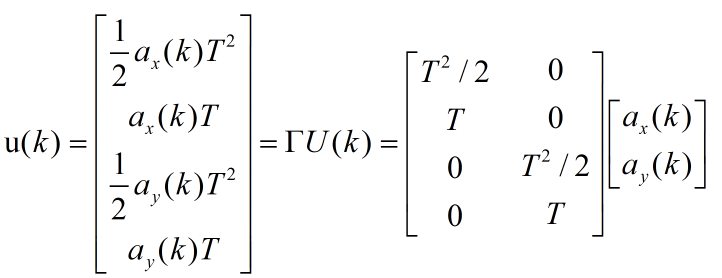
记过程噪声u(k)的均方差为:

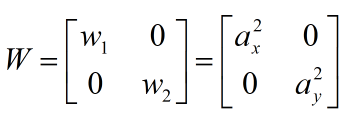
式中的w1和w2为一个可调节的参数，二者远远小于1.

 过程噪声u(k)的协方差为:

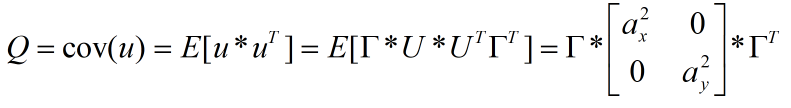
因此协方差与均方值之间的关系可以写为

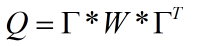
　　从模型来看状态方程是线性的，无需线性化求的状态转移矩阵F；但观测矩阵是一个非线性的，因此基于距离信息进行目标跟踪是一个非线性估计问题，因此要采用EKF对目标进行跟踪。 

运用线性化方法将非线性方程线性化。具体线性化可参考上一篇扩展KALMAN滤波（EKF）基本知识和相应的MATLAB仿真中的公式6和7.得到相应的雅可比矩阵。

 

 

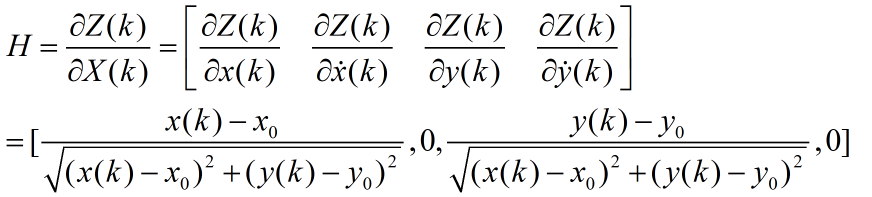
 上述所有方程基本上包含了EKF递推公式的所有结果。通过以上方程可以方便编写MATALB程序。

 

 1 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 2 %功能说明：扩展kalman滤波在目标跟踪中的应用
 3 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 4 clc
 5 clear all
 6 close all
 7 T=1;                   %雷达扫描周期
 8 N=100/T;               %采样次数
 9 X=zeros(4,N);          %目标真实位置、速度
10 X(:,1)=[-100 2 200 20];     %目标的起始位置和速度
11 Z=zeros(1,N);               %传感器测量的距离
12 delta_w=1e-3;               %若增大会变成曲线
13 W=delta_w*diag([0.5 1]);    %过程噪声方差
14 G=[T^2/2 0;T 0;0 T^2/2;0 T];        
15 R=4;                        %观测噪声方差
16 F=[1 T 0 0;0 1 0 0;0 0 1 T;0 0 0 1];    %状态转移矩阵
17 x0=200;y0=100;
18 Xstation=[200 100];                     %雷达的位置
19 for i=2:N
20    X(:,i)=F*X(:,i-1)+G*sqrt(W)*randn(2,1);     %目标的真实轨迹 
21 end
22 for i=1:N
23    Z(i)=Dist(X(:,i),Xstation)+sqrt(R)*randn(1,1);  %目标的观测轨迹
24 end
25 %EKF滤波
26 X_ekf=zeros(4,N);                %EKF滤波
27 X_ekf(:,1)=X(:,1);               %EKF初始化
28 P=eye(4);                        %协方差矩阵初始化。
29 I=eye(4);
30 for i=2:N
31     Xn=F*X_ekf(:,i-1);
32     Z1=Dist(Xn,Xstation);
33     %求解观测矩阵
34     H=[(Xn(1)-x0)/sqrtm((Xn(1)-x0)^2+(Xn(3)-y0)^2) 0 (Xn(3)-y0)/sqrtm((Xn(1)-x0)^2+(Xn(3)-y0)^2) 0];
35     P1=F*P*F'+G*W*G';
36     K=P1*H'/(H*P1*H'+R);
37     X_ekf(:,i)=Xn+K*(Z(i)-Z1);
38     P=(I-K*H)*P1;
39 end
40 %误差分析
41 for i=1:N
42     Err_Kalman(i)=Dist(X(:,i),X_ekf(:,i));
43 end
44 
45 %%%%%%画图
46 figure
47 plot(X(1,:),X(3,:),'k.');hold on;
48 plot(X_ekf(1,:),X_ekf(3,:),'r*');
49 legend('真实轨迹','EKF轨迹');
50 grid on;
51 xlabel('横坐标\m');
52 ylabel('纵坐标\m');
53 
54 figure
55 plot(Err_Kalman,'-ks');
56 xlabel('时间\s');
57 ylabel('位置估计偏差\m');

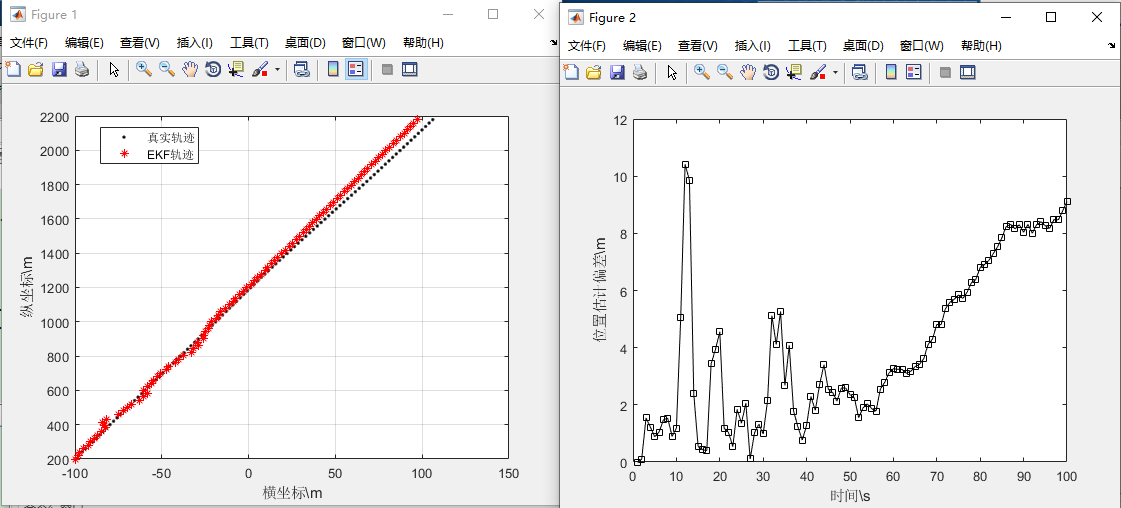
 仿真结果如下图所示