参考内容：书籍《卡尔曼滤波原理及应用------matlab仿真》这本书对kalman算法的解析很清晰，MATLAB程序很全，适合初学者（如有侵权，请联系删除(qq:1491967912)）
EKF滤波算法是建立在KF滤波算法的基础上，核心思想是，对于非线性系统，首先对滤波值
的非线性函数
展开成泰勒级数但只保存一阶及以下部分（舍去二阶和高阶部分），得到近似的线性化模型。然后就是利用KF算法完成对目标的滤波估计等处理。
EKF的优点是不需提前计算标准轨迹（过程噪声W（k）与观测噪声V（k）为0时的非线性方程的解），但它的缺陷是只能在滤波误差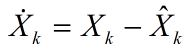
和一步预测误差
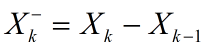较小的时候才能使用。
1、扩展kalman滤波原理
1.1 局部线性化
离散非线性系统动态方程可写为：
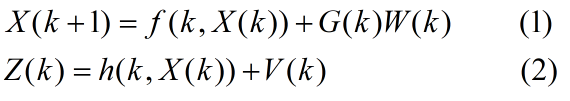
其中，当过程噪声W（k）和观测噪声V(k)恒为零时，模型1、2的解为非线性模型的理论解，称为“标称轨迹”或“标称状态”。另外，把非线性系统1、2的真实解称为“真轨迹”或“真实值”。
接下来是具体的数学推导。首先假定没有控制量的输入，过程噪声是均值为零的高斯白噪声，同时噪声的驱动矩阵G（k）是已知的，观测噪声V（k）是加性均值为零的高斯白噪声，并假定过程噪声W（k）和观测噪声V（k）二者之间相互独立。
首先进行的局部线性化的步骤，将EKF中的非线性模型局部线性化。这里会用到泰勒级数展开公式，关于泰勒级数的知识请参考如何通俗地解释泰勒公式？这里只给出泰勒公式的在0点的n阶展开公式：
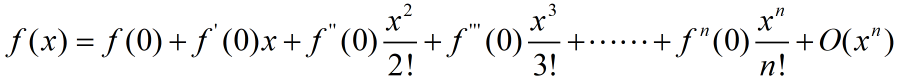根据系统状态方程1，将非线性函数f（*）围绕滤波值
做一阶泰勒展开，结果为：
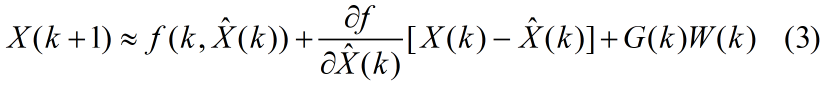令
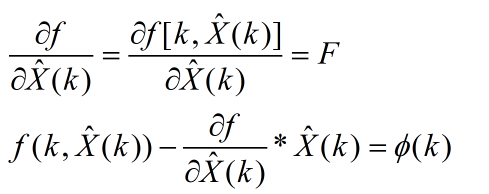将上面两个公式带入到公式3中得到线性化的状态方程为：
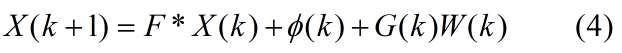状态初始值为X(0)=E[X(0)]。与KF算法相比，在已经求得前一步滤波值的条件下
，状态方程4增加了非随机的外作用项
。
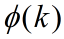另外由系统量测方程，将非线性函数h(*)围绕滤波值，做一阶泰勒展开。得
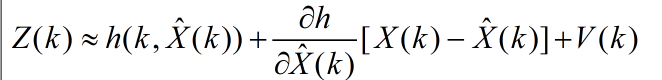
令：
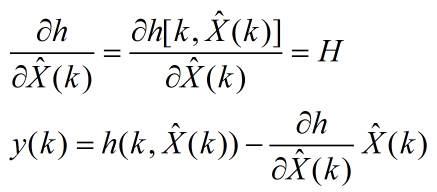
则观测方程为：
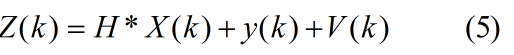
1.2、线性Kalman滤波
这样就将非线性化模型1、2转换为了线性化模型4、5，对这个线性化的模型应用kalman滤波基本方程可得扩展kalman滤波方程。
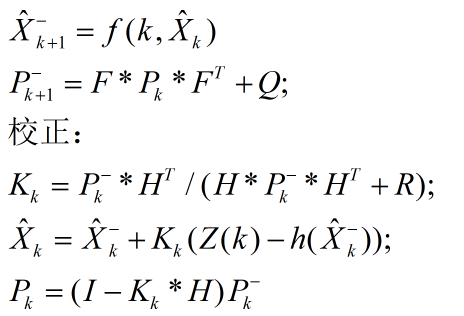
式中，滤波初值和滤波误差方差矩阵初值分别为：
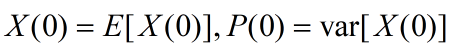
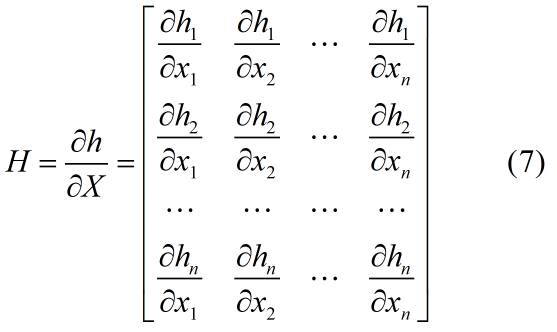
与kalman滤波基本方程相比，在线性化后的系统方程中，状态转移矩阵F和观测矩阵H由f和h的雅可比矩阵替代。假设状态变量有n维，即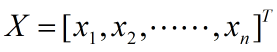
，则相应雅可比矩阵的求法如下。
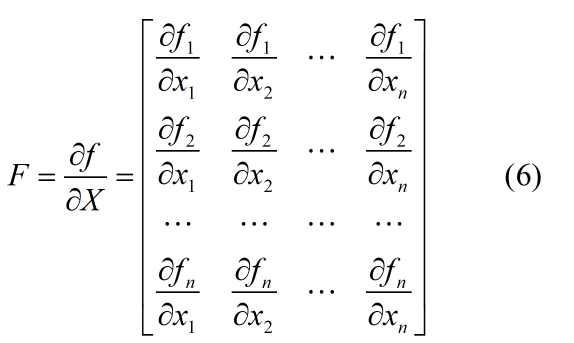
1.3、扩展Kalman滤波器九大步骤：
第一步：初始化初始状态方程X(0)、观测方程Z（0）、协方差矩阵P0；
第二步：状态预测：
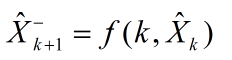第三步：观测预测：
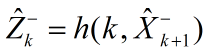第四步：一阶线性化状态方程，求解状态转移矩阵F。
第五步：一阶线性化观测方程，求解观测矩阵H。
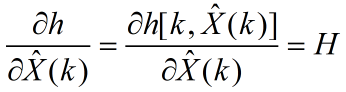第六步：求协方差矩阵预测
。
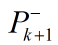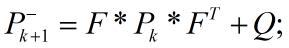
第七步：求Kalman滤波增益
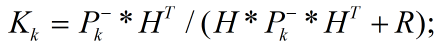
第八步：求状态更新
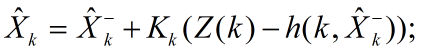
或者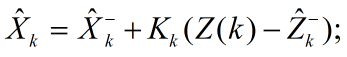
第九步：协方差更新
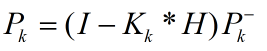
上面的九个步骤就是EKF设计的一个计算周期，各个时刻EKF对非线性系统的处理就是这个计算周期不断循环的过程。
2、matlab仿真程序
假设总时间为50s，过程噪声方差Q=5；观测噪声方差R=2；系统的状态方程和观测方程为：
状态方程：X（k+1）=0.5X(k)+2.5X(k)/(1+X(k)^2)+8cos(1.2k)+w(k)
观测方程：Z(k)=X(k)^2/20+v(k)
其中w(k)、v(k)是对应的过程噪声和观测噪声。假设初值X（0）=0.1，协方差的初值为P=1;具体程序如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%函数功能：标量非线性扩展kalman滤波问题
%状态方程：X（k+1）=0.5X(k)+2.5X(k)/(1+X(k)^2)+8cos(1.2k)+w(k)
%观测方程：Z(k)=X(k)^2/20+v(k)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
close all
T=50; %总时间
Q=5; %Q值的改变会得到不同的滤波结果
R=2; %测量噪声
%产生过程误差
w=sqrt(Q)*randn(1,T);
%产生测量噪声
v=sqrt(R)*randn(1,T);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%状态方程
X=zeros(1,T);
X(1)=0.1; %状态方程初始化
Z=zeros(1,T);
Z(1)=X(1)^2/20+v(1); %测量方程初始化
for i=2:T
X(i)=0.5*X(i)+2.5*X(i)/(1+X(i)^2)+8*cos(1.2*i)+w(i);
Z(i)=X(i)^2/20+v(i);
end
Xekf=zeros(1,T);
Xekf(1)=X(1);
I=eye(1);
P=[1];
for i=2:T
Xekf(i)=0.5*X(i)+2.5*X(i)/(1+X(i)^2)+8*cos(1.2*i); %状态预测
Z1(i)=X(i)^2/20;
F=0.5+2.5*(1-Xekf(i))/(1+Xekf(i)^2)^2; %求解状态转移矩阵
H=Xekf(i)^2/20; %求解观测矩阵
P1=F*P*F+Q;
K=P1*H'/(H*P1*H'+R);
X(i)=Xekf(i)+K*(Z(i)-Z1(i));
P=(I-K*H)*P1;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%%%%误差分析
Xstd=zeros(1,T);
for i=1:T
Xstd(i)=abs(X(i)-Xekf(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%画图
figure;
hold on;box on;
plot(X,'-ko','MarkerFace','g');
plot(Xekf,'-bs','MarkerFace','r');
legend('真实值','EKF滤波的估计值');
xlabel('时间\s');
ylabel('状态值');
%误差分析
figure;
hold on;box on;
plot(Xstd,'-ko','MarkerFace','g');
xlabel('时间\s');
ylabel('状态估计偏差');
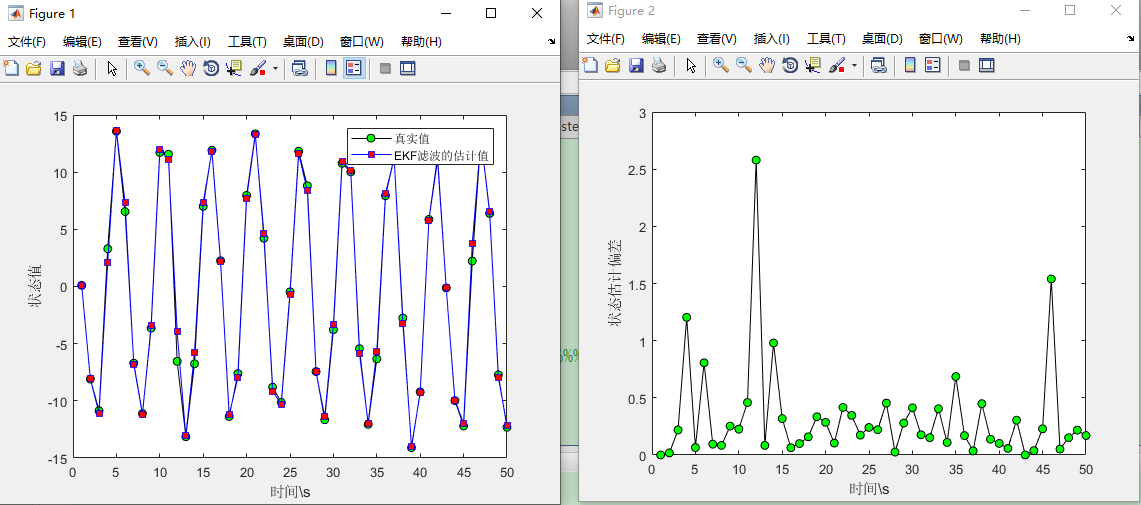
以上就是关于扩展Kalman滤波的全部原理和公式如果有错误还请批评指正。
