参考内容：B战的DR_CAN的卡尔曼滤波器视频，讲的特别的好，建议要学习的可以去看看，非常通俗易懂，很好理解。
1、初见卡尔曼滤波器-----递归运算
卡尔曼滤波器用一句话来说是一种 optimal recursive data processing algorithm
最优化 递归 数字处理 算法
卡尔曼滤波器更像是一个观测器，而不像传统意义上的滤波器。
卡尔曼滤波器的应用非常广泛，尤其在导航中，之所以会广泛运用是因为生活中存在大量的不确定性，当描述一个系统时这种不确定性主要分为三类。
1、不存在完美的数学模型
不确定性：2、系统的扰动不可控，也很难建模
3、测量传感器哦存在误差
例：
不同的人测量硬币的直径，用Zk表示测量的结果，下标k代表第几次测量的结果，由于每个人测量的结果和尺子的误差可能会不一样，例如Z1=50.1mm,Z2=50.5mm,Z3=50.6mm。若要你估计一下真实结果，你可能第一时间会对上面的三个数据直接取平均值。
估计值
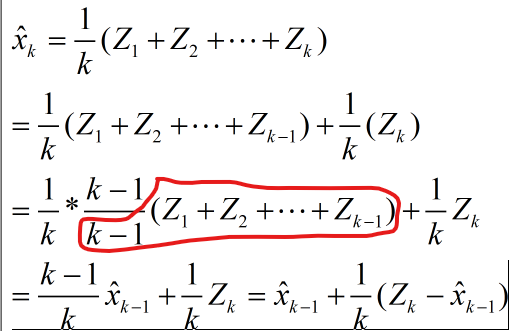
随着k的不断增大，1/k不断趋近于0，此时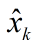
趋近于
，可以看出随着k的增加，测量的结果就不重要了。当k比较小的时候，1/k会比较大，测量的结果就非常重要。
令1/k=kk
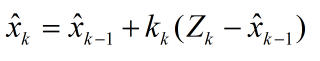
它的意思是： 当前的估计值=上一次估计值+系数*（当前测量值-上一次估计值）；
kk在卡尔曼滤波中称为：卡尔曼增益
两个参数：
估计误差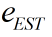
（估计值与真实值之间的误差）、测量误差
（测量值与真实值之间的误差）；
（第k-1次的估计误差）除以（第k-1次的估计误差+第k次的测量误差）。
讨论：在k时刻，
1、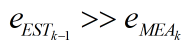
：当k-1次的估计误差远远大于第k次的测量误差，kk趋近于1，此时第k次的估计值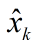趋近于第k次的测量值
。
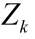2、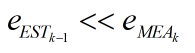
：当k-1次的估计误差远远小于第k次的测量误差，kk趋近于1，此时第k次的估计值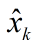趋近于第k-1次的估计值。
卡尔曼思想解决一个简答问题：
step1:计算卡尔曼增益：
step2：计算估计值：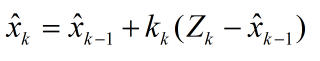
step3:更新估计误差（非常重要，之后推导）：
下面是一个简单的例子。
图中的数据就是按照这三个步骤逐步出来的结果，图右侧是数据画出数据结果，其中蓝色的线是测量值的结果，另外一条是估计的结果，可以看出估计出的结果很快就趋近与实际值50，并且很稳定。
第一节初始卡尔曼滤波先到这，后面会具体对卡尔曼滤波进行推导。如果有错误的地方还请批评指正。谢谢。
