线性代数3 伴随矩阵和可逆矩阵

1.伴随矩阵的概念和公式

复习：
称Aij = (-1)^i+j×Mij为行列式元素aij的代数余子式
aij的余子式Mij为原行列式中去除第i行和第j列后形成的n-1阶的行列式。
矩阵对应的行列式的写法：如果用A代表矩阵，则|A|代表的是A对应的行列式（并且为了区分，一般在写行列式的时候都会加上绝对值符号）

伴随矩阵的概念：
由矩阵A的行列式|A|的所有代数余子式（每个元素对应一个）所构成的矩阵称为矩阵A的伴随矩阵，记为A*

（伴随矩阵其实是在求逆矩阵A^-1时引入的一个过程性概念，详细理解逆矩阵的概念和意义之后就会理解伴随矩阵的意义）
计算伴随矩阵的过程就是计算矩阵对应的行列式的所有代数余子式的过程，要注意是代数余子式而不是余子式。

伴随矩阵相关公式：

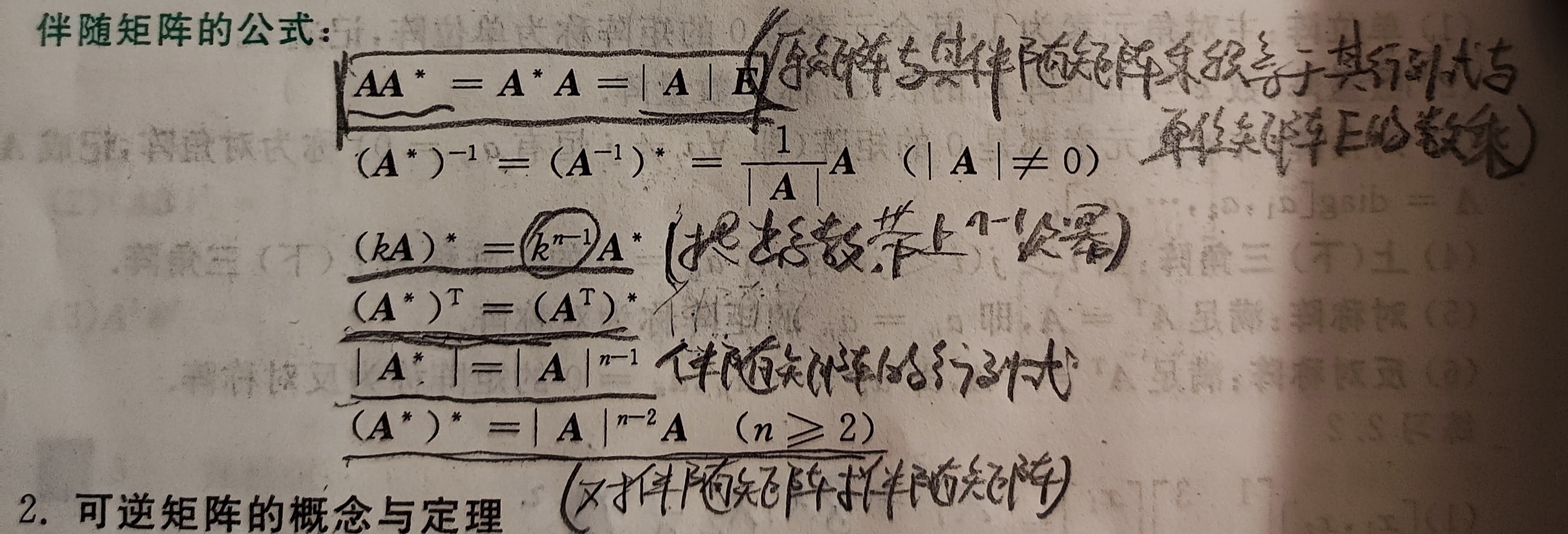
2.可逆矩阵的概念和定理

可逆矩阵的概念：
对于n阶方阵A，若存在一个n阶矩阵B使 AB = BA = E
则称A是可逆矩阵（或非奇异矩阵），称B为A的逆矩阵，即B = A^-1.

关于这个概念：
1.可逆矩阵首先必须是方阵，因为不是方阵的话矩阵相乘不符合交换律，就不可能有AB = BA
2.若B为A的逆矩阵，A是可逆矩阵；则也可以反过来说A为B的逆矩阵，B也是可逆矩阵。

与可逆矩阵相关的定理：
定理1：若矩阵A可逆，则A的逆矩阵唯一
定理2：矩阵A可逆 等价于 A的行列式|A|≠0
即：矩阵可逆能推出其行列式不为0；反之由矩阵行列式不为0 能推出矩阵可逆。
定理3：对于n阶矩阵A和B，若AB=E，则必有BA=E。

3.n阶矩阵可逆的充要条件

这五个条件都是n阶矩阵A可逆的充要条件


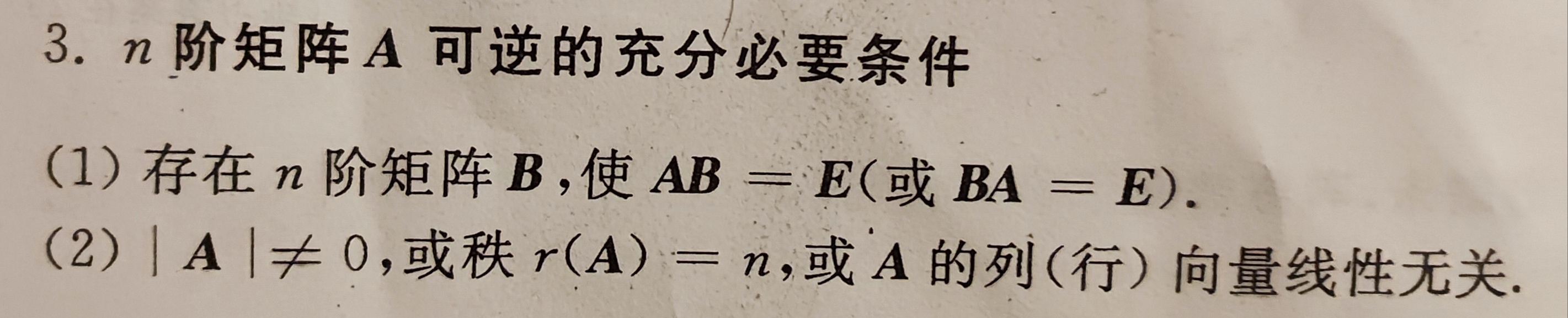
解释：
1比较容易理解，基本上就是矩阵可逆的定义。
2中的矩阵的秩，向量线性无关等概念在后面会学习
3中，Ax = 0其实就相当于矩阵A的行列式≠0
4
5矩阵的特征值在后面会学到

4.逆矩阵的运算性质

（1）若k≠0且矩阵A可逆，则：
(k×A)^-1 = 1/k × A^-1
(矩阵的系数在求逆时可以提出到括号外，提出后系数变为原来的倒数）
（2）若矩阵A，B都可逆，则：
(AB)^-1 = B^-1 × A^-1
对相乘的两个矩阵整体求逆的结果。
要注意结果中的运算顺序，AB求逆后，结果为B^-1乘A-1
特殊情况: (A²⁾-1 = (A^-1)2
(即为A与B相等的情况)
（3）矩阵求逆与转置的运算法则
若A的转置可逆，则(A^T)-1 = (A^-1)T
即：矩阵的先转置后求逆与先求逆后转置的结果是一样的。
（4）对矩阵两次求逆，则会得到原矩阵
（5）对于可逆矩阵A：
A的逆矩阵的行列式值等于A的行列式的倒数

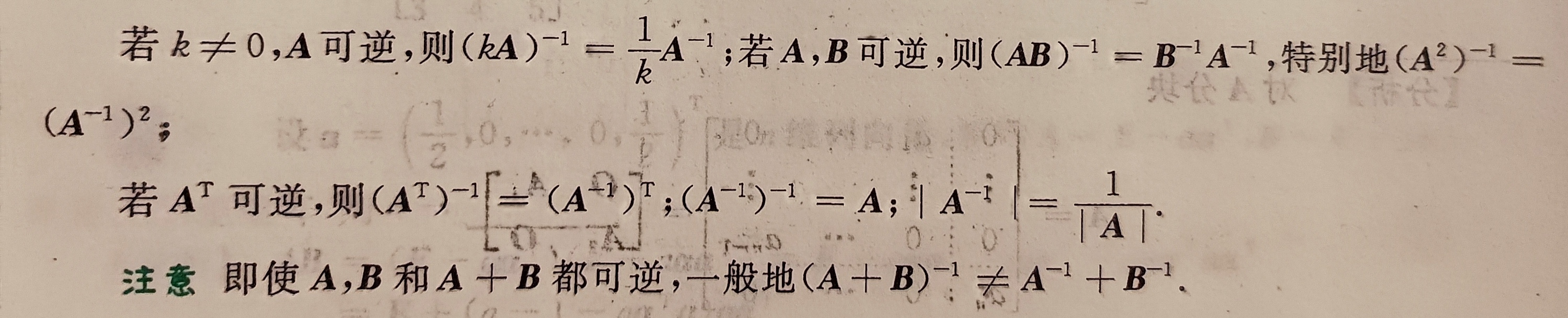
最后补充了一点：矩阵之和的逆矩阵不等于两个矩阵的逆矩阵之和

5.矩阵求逆的几种常用方法总结

1将求逆转化为求行列式和伴随矩阵的过程
2 初等变换还没学到
3 找一个能满足定义的矩阵B，应该只适用于比较简单或者特殊的矩阵
4 分块矩阵还没学到，应该是利用分块矩阵求逆的法则将复杂的矩阵求逆转换为简单的矩阵