数学 多元函数微分学 多元函数的极值与最值

一，无条件极值

1.极值/极值点的定义：f(x,y)在某点的某邻域内值最大/最小，则称f(x,y)在这点取得极大值/极小值（极值指的是函数值），这一点(x0,y0)称为极值点。极大值/极小值统称为极值。

2.多元函数取极值的必要条件：多元函数取得极值 => 该点处偏导数若存在则必为0

驻点的概念：偏导数等于零的点称为驻点。（是由坐标(x,y)确定的点）

3.用偏导数判断极值情况（多元函数取得极值的充分情况）

 <h4>二，条件极值</h4>

指的是函数f(x,y)在某个方程式作为限制条件之下的极值

根据这种方法直接解就行。

<h4>三，最值问题</h4>

求最值一般分为三步进行：求出所有极值点的可能点，在求出边界上的最值，将所有这些最值可能点进行比较得出最终的最值。

这里一定要注意考虑边界上的值，这就是求最值与求极值的区别。

一般在求边界时需要用到条件极值来求（构造拉格朗日函数）

 最值问题比较容易考应用题，在这个过程中比较重要的是根据问题建立目标函数，以及处理边界值

 

---

 

例题：关于几何的最值问题

1.

建立目标函数后的计算步骤和一般求最值的步骤相同。

*拉格朗日函数 用于求空间内任意一点到曲面上的点的最短距离：

L=D+λ*F

其中D表示空间内点到曲面上点的距离的平方(x-x0)^2+(y-y0)^2+(z-z0)^2，F(x,y,z)即为曲面的函数表达式

要注意，这里λ也是L的一个变量，也就是距离函数为L(x,y,z,λ)

求极值时要对这四个变量都求偏导，并令偏导等于0，得出最值点的可能点。

2.**几何公式：平面内点到直线的距离**

 3.平面内直线的两点式

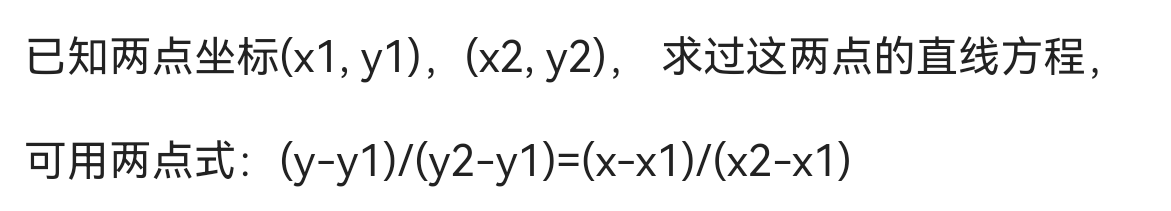
 4.平面内两点间距离