[CodeForces - 1225F]Tree Factory【树】【dfs】【贪心】
[CodeForces - 1225F]Tree Factory【树】【dfs】【贪心】
标签:codeforces题解 贪心 树 dfs
题目描述
Time limit
2000 ms
Memory limit
524288 kB
Source
Technocup 2020 - Elimination Round 2
Tags
constructive algorithms greedy trees *2500
题面

Input1
5
0 0 1 1
Output1
0 2 1 4 3
2
1 3
Input2
4
0 1 2
Output2
0 1 2 3
0
题目大意
将一棵竹子(链)变成一棵树的操作:可以将这棵树中的任意非根结点接到它的祖父结点(前驱的前驱)上,且这个结点的子孙全不变。
题目中给定结点数,和除根结点外每个结点的父节点,即给定一棵树。问什么样的竹子(链)变成这棵树所花费的操作数最少。输出这棵竹子,操作数,和每次需要操作操作的结点。
例如,
给定一棵树
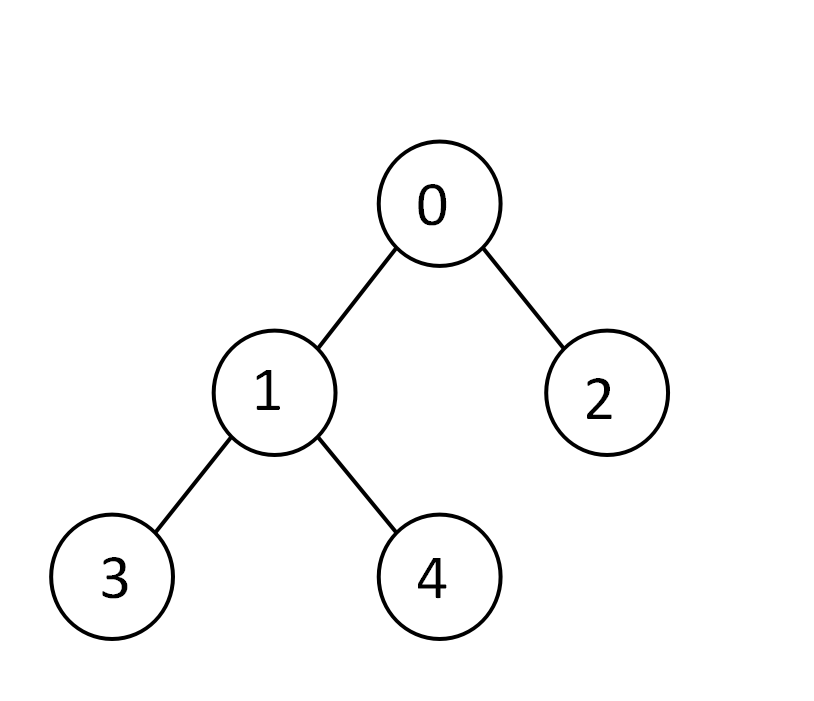
生成它所需操作数最少的竹子(链)为
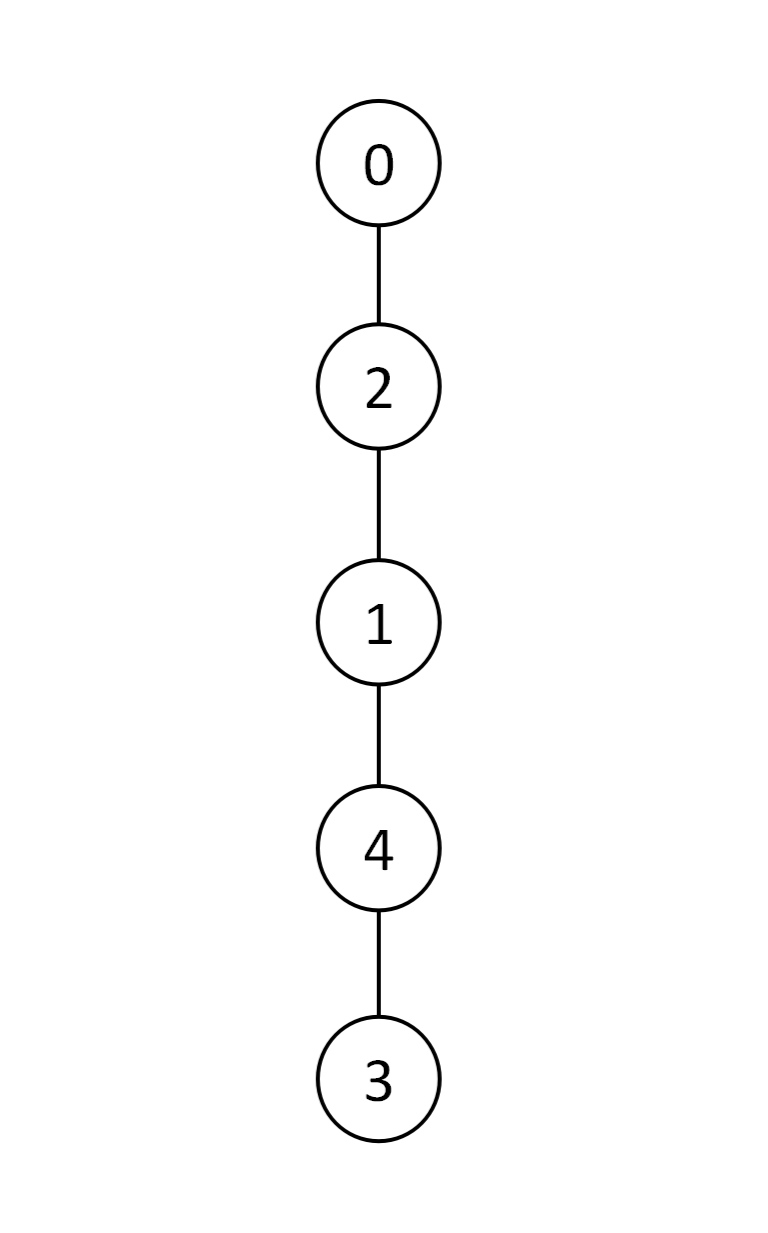
需要依次对1结点和3结点操作
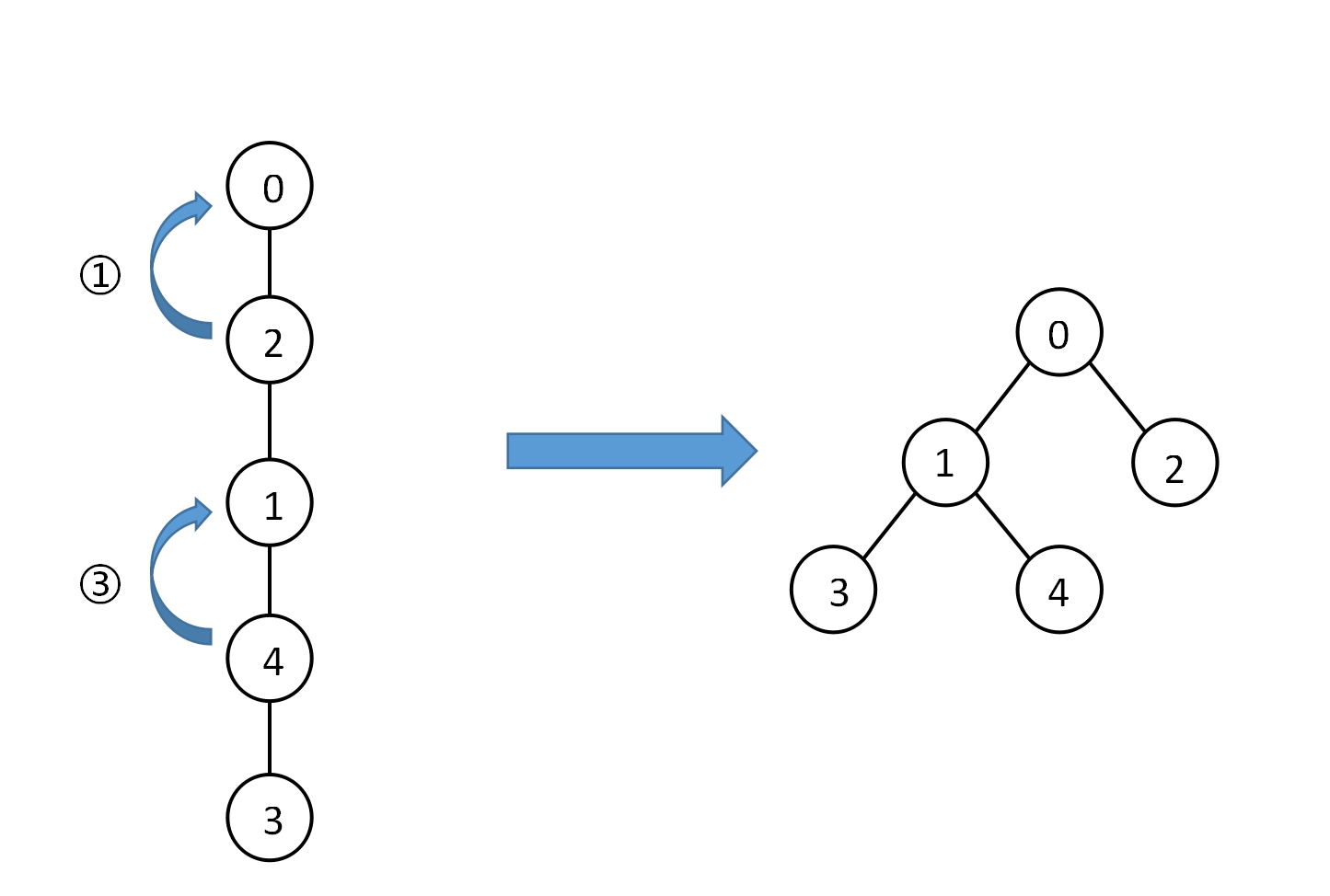
解析
-
题目问的是要由链生成树,其实我们首先要做的是由给定的这棵树生成操作数最少的链。
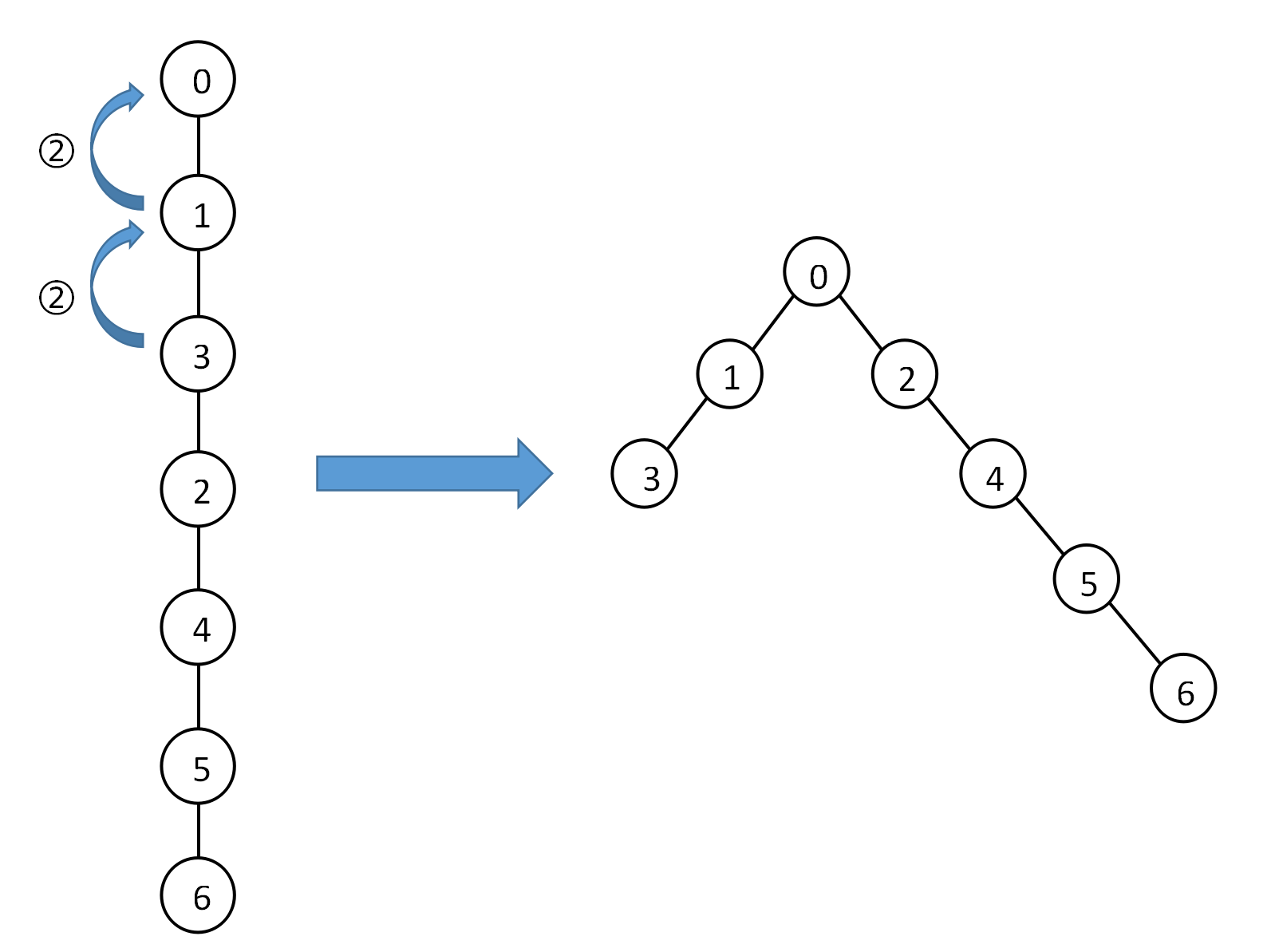
我们先从简单的问题开始思考,给定一棵如下二叉树。根节点的左子树高度小于右子树。
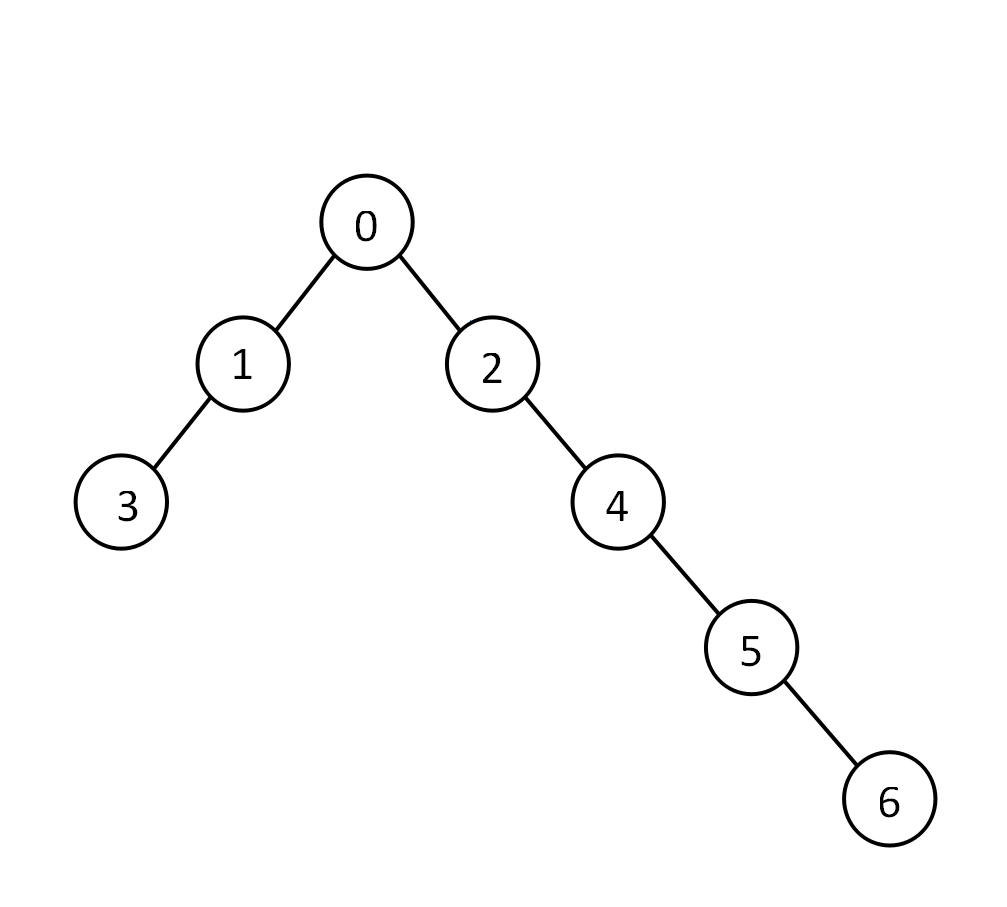
将2结点接到3结点的后面,生成0132456的链,操作数为2。
将1结点接到6结点的后面,生成0245613的链,操作数为4。
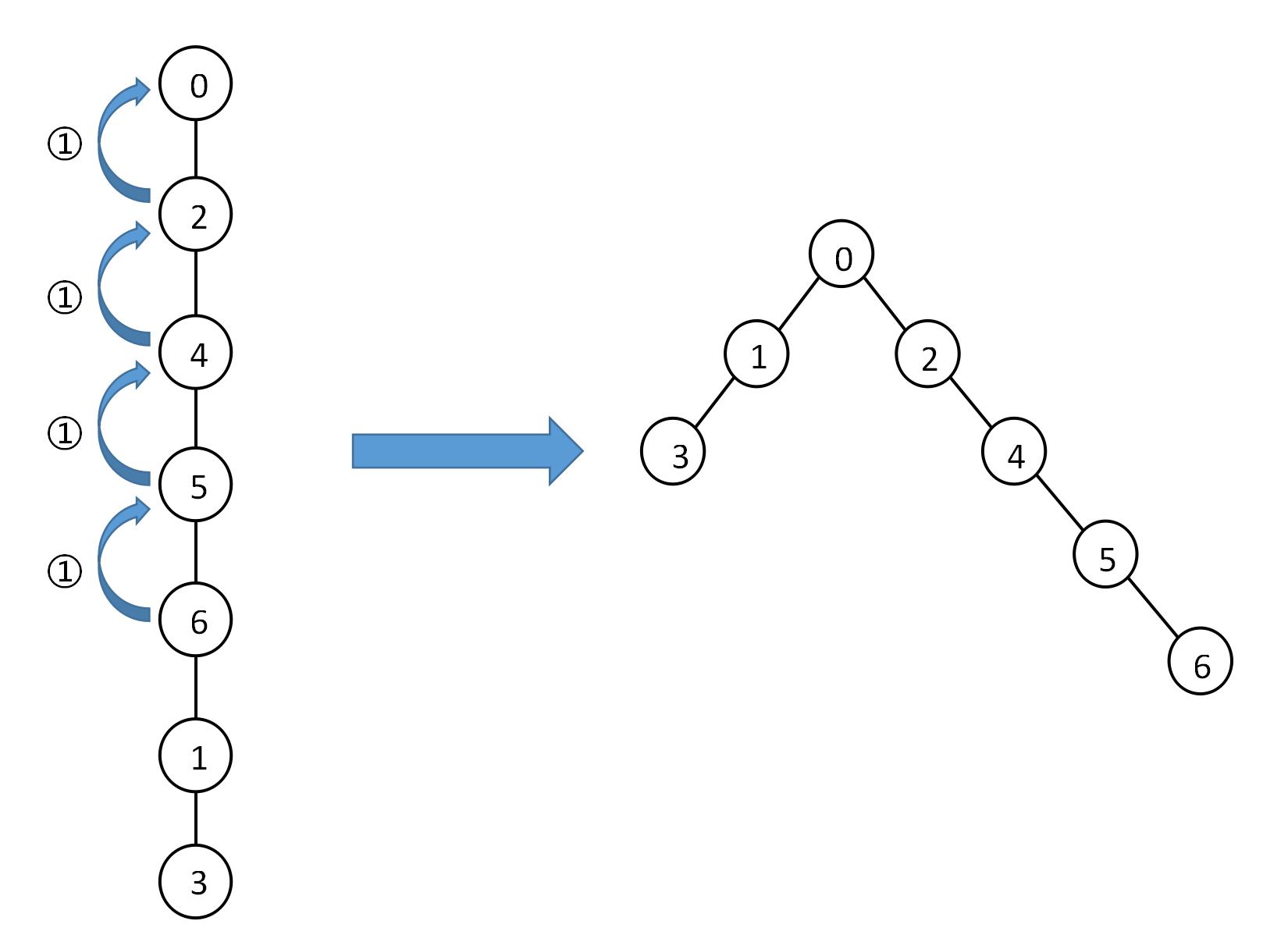
由上述的例子可见,对于一个结点,如果它的左子树高度小于右子树,需要把它的右子树全部接到左子树之后;如果它的右子树高度小于左子树,需要把它的左子树全部接到右子树之后。这个结论同样也可以推广到普通树,对于一个结点,应该按其子树高度将各个子树依次相接。 -
建好了链,下面的问题是如何通过操作将这个链还原为树。
设\(a[1 \cdots n]\)为链的次序,\(p[u]\)为链中结点\(u\)的前驱结点,\(fa[u]\)为树中结点\(u\)的父亲结点。
从\(a[1]\)开始循环到\(a[n]\),依次对每个结点\(a[i]\)进行操作。如果\(a[i]\)的链中前驱\(p[a[i]]\)不是它树中的父亲结点\(fa[a[i]]\),就进行一次操作把\(a[i]\)接到\(a[i]\)的前驱的前驱上。并记录下a[i]。每次操作\(p[a[i]]\)的值都改变。
循环的次序为什么是有序的,不能反着来?
因为反着来无法保证最优解。链\(a[1 \cdots n]\)本身就是高度小的子树在左边,高度大的子树在右边。只有按照\(a[1]\)到\(a[n]\)(从左到右)的顺序进行操作,才能保证每个子树还原的操作数是最小的。
通过代码
/*
Status
Accepted
Time
93ms
Memory
10572kB
Length
1525
Lang
GNU G++11 5.1.0
Submitted
2020-01-13 17:20:42
RemoteRunId
68700673
*/
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 50;
int fa[MAXN], p[MAXN], high[MAXN], a[MAXN], n, cnt = 0;
vector<int> e[MAXN], ans;
inline int read() //1e5的数据量,使用快读.
{
int res = 0;
char ch;
ch = getchar();
while(!isdigit(ch))
ch = getchar();
while(isdigit(ch)){
res = (res << 3) + (res << 1) + ch - 48;
ch = getchar();
}
return res;
}
inline bool cmp(int i, int j)
{
return high[i] < high[j];
}
void dfs1(int u) //第一次dfs,算出每个结点的高度.
{
if(!e[u].size()){
high[u] = 1;
return;
}
for(int i = 0; i < e[u].size(); i ++)
dfs1(e[u][i]);
int maxx = 0;
for(int i = 0; i < e[u].size(); i ++)
maxx = max(maxx, high[e[u][i]]);
high[u] = maxx + 1;
return;
}
void dfs2(int u) //第二次dfs找出链的顺序a[1..n].
{
a[++ cnt] = u;
sort(e[u].begin(), e[u].end(), cmp); //按照子树高度由小到大排序.
for(int i = 0; i < e[u].size(); i ++)
dfs2(e[u][i]);
return;
}
int main()
{
n = read();
for(int i = 1; i < n; i ++){
int t;
t = read();
e[t].push_back(i); //由父结点指向儿子的边.
fa[i] = t; //i的父亲是t.
}
dfs1(0); //两次dfs找到链.
dfs2(0);
for(int i = 1; i <= n; i ++)
printf("%d%c", a[i], i == n? '\n': ' ');
for(int i = 2; i <= n; i ++)
p[a[i]] = a[i - 1]; //预处理p[1...n]数组.
for(int i = 2; i <= n; i ++){ //进行还原.
int u = a[i];
while(p[u] != fa[u]){
ans.push_back(u); //每次操作都记录下a[i],存在ans中.
p[u] = p[p[u]];
}
}
printf("%d\n", ans.size());
for(int i = 0; i < ans.size(); i ++)
cout << ans[i] << " " ;
return 0;
}


