tarjan图论算法

tarjan图论算法

标签： tarjan 图论 模板

---

洛谷P3387 【模板】缩点

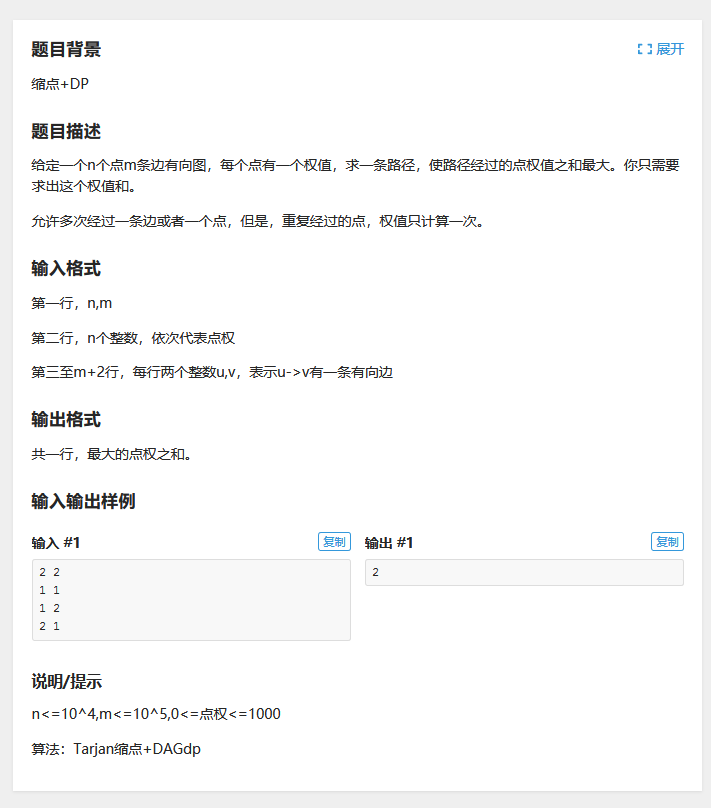
算法：Tarjan有向图强连通分量+缩点+DAGdp

代码：

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
#define psk push_back
using namespace std;

const int MAXN = 1e5 + 50;

int dfn[MAXN], low[MAXN], dfscnt = 0, scccnt = 0;
int sccnum[MAXN], s[MAXN], in[MAXN], top = 0;
int p0[MAXN], p[MAXN], d[MAXN];

vector<int> G[MAXN], G0[MAXN];
queue<int> q;

inline int read()
{
    int res = 0, f = 1;
    char ch;
    ch = getchar();

    while(!isdigit(ch)){
        if(ch == '-')
            f = -1;

        ch = getchar();
    }

    while(isdigit(ch)){
        res = res * 10 + ch - 48;

        ch = getchar();
    }

    return f * res;
}
void tarjan(int now)
{
    dfn[now] = low[now] = ++ dfscnt;
    s[top ++] = now;

    for(int i = 0; i < G0[now].size(); i ++){
        int v = G0[now][i];

        if(!dfn[v]){
            tarjan(v);
            low[now] = min(low[now], low[v]);
        }
        else if(!sccnum[v])
            low[now] = min(low[now], dfn[v]);
    }

    if(low[now] == dfn[now]){

        scccnt ++;

        do{
            sccnum[s[-- top]] = scccnt;
        }while(s[top] != now);

    }
    return;
}

int topoo()
{

    for(int i = 1; i <= scccnt; i ++)
        if(!in[i]){
            d[i] = p[i];
            q.push(i);


        }


    while(!q.empty()){
        int u = q.front();q.pop();

        for(int i = 0; i < G[u].size(); i ++){
            int v = G[u][i];

            if(d[v] < d[u] + p[v])
                d[v] = d[u] + p[v];

            in[v] --;

            if(!in[v])
                q.push(v);
        }
    }

    return *max_element(d + 1, d + 1 + scccnt);
}


int main()
{
    int n, m;

    n = read(), m = read();

    for(int i = 1; i <= n; i ++)
        p0[i] = read();

    for(int i = 0; i < m; i ++){
        int u, v;

        u = read(), v = read();

        G0[u].psk(v);
    }

    for(int i = 1; i <= n; i ++)
        if(!dfn[i])
            tarjan(i);

    for(int i = 1; i <= n; i ++){
        p[sccnum[i]] += p0[i];

        for(int j = 0; j < G0[i].size(); j ++){
            int v = G0[i][j];
            if(sccnum[i] == sccnum[v])
                continue;
            G[sccnum[i]].psk(sccnum[v]);

            in[sccnum[v]] ++;
        }
    }

    printf("%d", topoo());

    return 0;
}

---

洛谷P3388 【模板】割点（割顶）

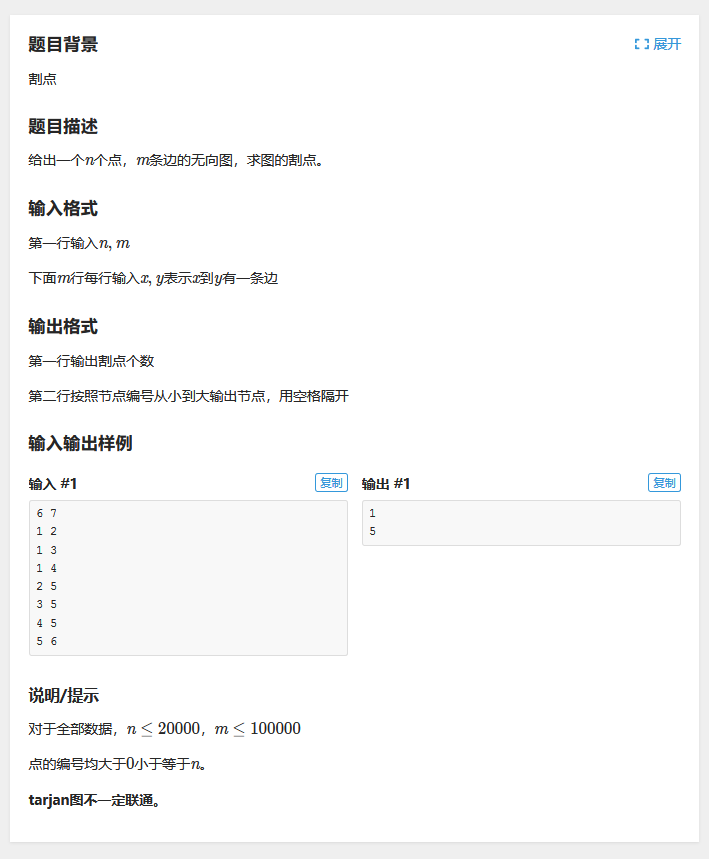
算法：tarjan求无向图割点割边
代码：

#include <cstdio>
#include <cstring>
#include <vector>
#include <iostream>
#define pbk push_back
using namespace std;

const int MAXN = 1e5 + 50;

int dfn[MAXN], low[MAXN], n, m;
int dfscnt = 0, iscut[MAXN];

vector<int> G[MAXN];

inline int read()
{
    int res = 0, f = 1;

    char ch;

    ch = getchar();

    while(!isdigit(ch)){
        if(ch == '-')
            f = -1;

        ch = getchar();
    }


    while(isdigit(ch)){
        res = (res << 3) + (res << 1) + ch - 48;

        ch = getchar();
    }

    return f * res;
}
void tarjan(int now, int rt)
{
    int chcnt = 0;

    dfn[now] = low[now] = ++ dfscnt;

    for(int i = 0; i < G[now].size(); i ++){
        int v = G[now][i];

        if(!dfn[v]){
            tarjan(v, rt);
            low[now] = min(low[now], low[v]);

            if(now == rt)
                chcnt ++;
            else if(low[v] >= dfn[now])
                iscut[now] = 1;
        }

        else
            low[now] = min(low[now], dfn[v]);
    }

    if(chcnt >= 2)
        iscut[now] = 1;
    return;
}

int main()
{
    int n, m, tot = 0;

    n = read(), m = read();

    for(int i = 0; i < m; i ++){
        int u, v;

        u = read(), v = read();

        G[u].pbk(v);
        G[v].pbk(u);
    }

    for(int i = 1; i <= n; i ++)
        if(!dfn[i])
            tarjan(i, i);

    for(int i = 1; i <= n; i ++)
        if(iscut[i])
            tot ++;
    printf("%d\n", tot);
    for(int i = 1; i <= n; i ++)
        if(iscut[i])
            printf("%d ", i);

    return 0;
}

---

求无向图边双连通分量

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
#define pbk push_back
using namespace std;

const int MAXN = 1e5 + 50;

vector<int> G[MAXN], bcc[MAXN];

int low[MAXN], dfn[MAXN], bnum[MAXN], s[MAXN];
int n, m, top = 0, dfscnt = 0, bcnt = 0;

inline int read()
{
    int res = 0, f = 1;
    char ch;

    ch = getchar();

    while(!isdigit(ch)){
        if(ch == '-')
            f = -1;

        ch = getchar();
    }

    while(isdigit(ch)){
        res = (res << 3) + (res << 1) + ch - 48;

        ch = getchar();
    }

    return f * res;
}
void tarjan(int now, int fa)
{
    dfn[now] = low[now] = ++ bcnt;
    s[top ++] = now;

    int flag = 0;
    for(int i = 0; i < G[now].size(); i ++){
        int v = G[now][i];

        if(v == fa && !flag){
            flag = 1;
            continue;
        }

        if(!dfn[v]){
            tarjan(v, now);
            low[now] = min(low[now], low[v]);
        }
        else if(!bnum[v])
            low[now] = min(low[now], dfn[v]);
    }

    if(low[now] == dfn[now]){
        bcnt ++;

        do{
            bnum[s[-- top]] = bcnt;
            bcc[bcnt].pbk(s[top]);
        }while(s[top] != now);
    }

    return ;
}
int main()
{
    n = read(), m = read();

    for(int i = 0; i < m; i ++){
        int u, v;

        u = read(), v = read();

        G[u].pbk(v);
        G[v].pbk(u);
    }

    for(int i = 1; i <= n; i ++)
        if(!dfn[i])
            tarjan(i, 0);

    printf("%d\n", bcnt);

    for(int i = 1; i <= bcnt; i ++){

        printf("%d ", i);

        for(int j = 0; j < bcc[i].size(); j ++)
            printf("%d ", bcc[i][j]);
        printf("\n");
    }
    return 0;
}

---

求无向图点双连通分量

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
#define pbk push_back
using namespace std;

const int MAXN = 1e5 + 50;

int low[MAXN], dfn[MAXN], n, m;
int s[MAXN], top = 0, bcnt = 0, dfscnt = 0;

vector<int> G[MAXN], bcc[MAXN];

inline int read()
{
    int res = 0, f = 1;

    char ch;

    ch = getchar();

    while(!isdigit(ch)){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }

    while(isdigit(ch)){
        res = (res << 3) + (res << 1) + ch - 48;

        ch = getchar();
    }

    return f * res;
}
void tarjan(int now, int rt)
{
    low[now] = dfn[now] = ++ bcnt;

    s[top ++] = now;
    if(now == rt && !G[now].size()){
        bcc[++ bcnt].pbk(s[-- top]);
        return ;
    }
    for(int i = 0; i < G[now].size(); i ++){
        int v = G[now][i];

        if(!dfn[v]){
            tarjan(v, rt);
            low[now] = min(low[now], low[v]);

            if(low[v] >= dfn[now]){
                do{
                    bcnt ++;

                    bcc[bcnt].pbk(s[--top]);
                }while(s[top] != v);

                bcc[bcnt].pbk(now);
            }
        }
        else
            low[now] = min(low[now], dfn[v]);
    }
    return;

}

int main()
{
    n = read(), m = read();

    for(int i = 0; i < m; i ++){
        int u, v;
        u = read(), v = read();

        G[u].pbk(v);
        G[v].pbk(u);
    }


    for(int i = 1; i <= n; i ++){
        if(!dfn[i])
            tarjan(i, i);

    }

    for(int i = 1; i <= bcnt; i ++){
        printf("%d ", i);
        for(int j = 0; j < bcc[i].size(); j ++)
            printf("%d ", bcc[i][j]);
        printf("\n");
    }

    return 0;
}