FlashAttention逐代解析与公式推导

Standard Attention

标准Attention计算可以简化为：

\[O = softmax(QK^T)V \tag{1} \]

此处忽略了Attention Mask和维度归一化因子\(1/\sqrt{d}\)。

公式(1)的标准计算方式是分解成三步：

\[S = QK^T \tag{2} \]

\[P=softmax(S) \tag{3} \]

\[O = PV \tag{4} \]

但这样做的问题在于，假设\(Q,K,V \in R^{N\times d}\)，其中\(N\)为序列长度，\(D\)为注意力头的维度，那么输出\(O \in R^{N\times d}\)，\(S,P\in R^{N\times N}\)。由于在标准实现下，\(S,P\)都需要从HBM中读写，因此构成了\(O(N^2)\)的内存复杂度。一般情况下\(N\gg D\)，例如GPT-2中，\(N=1024\)，\(d=64\)，因此\(S\)和\(P\)的\(O(N^2)\)显存开销是远大于\(Q,K,V,O\)的\(O(Nd)\)的。

一个朴素的想法是：我们能否不进行\(O(N^2)\)的HBM读写，通过避免这一频繁的读写操作来大大提升Attention的计算效率。

Online Softmax

假设我们不将\(S,P\)写回HBM，那么就得将其放在片上SRAM中。但是这里的问题是片上SRAM受限于容量，一般无法一次性完整的计算Attention，因此我们必须采用分块（Tiling）操作，使得分块后的内存需求不超过SRAM的大小。但计算softmax的时候，其归一化因子（分母）需要所有的输入数据，因此进行分块计算的难度较大。

考虑softmax的公式，对于输入序列\(x\)：

\[x=[x_1,x_2,...,x_d] \tag{5} \]

原生softmax函数为：

\[softmax(x_i)=\frac{e^{x_i}}{\sum_{j=1}^{d}e^{x_j}} \tag{6} \]

为了避免数值溢出的问题，现在一般采用safe softmax的方式，即定义：

\[m(x)=max([x_1,x_2,...,x_d]) \tag{7} \]

safe softmax函数在e指数上减去\(m(x)\)，使得所有的e指数项的值分布在0到1之间（因为\(x_i-m(x)\leq 0\)），从而规避数值溢出的问题，此外还能提升数值稳定性，加快计算速度。改造后的函数为：

\[softmax(X)=\frac{e^{x_i-m(x)}}{\sum_{j=1}^{d}e^{x_j-m(x)}} \tag{8} \]

接下来我们需要研究如何对safe softmax应用分块策略来计算，即所谓的online softmax。

标准的softmax情况下，算法为：

for i = 1 to N do:

\[m_i\leftarrow max(m_{i-1},x_i) \tag{9} \]

end

for i = 1 to N do:

\[d_i \leftarrow d_{i-1}+e^{x_i-m_N} \tag{10} \]

end

for i = 1 to N do:

\[a_i \leftarrow \frac{e^{x_i-m_N}}{d_N} \tag{11} \]

end

可以看到这个计算过程需要三次1到N的循环，在Attention中，这里的\(x_i\)来自于\(QK^T\)，由于我们没办法在SRAM中装下\(Q\)和\(K\)，因此我们需要从内存中访问他们三次。假如我们能够想办法将\((9)\)到\((11)\)放到一个循环中，我们就能将访存从三次减少到一次。然而，由于\((9)\)和\((10)\)之间存在依赖，因为\((10)\)中包含一个不到最后一次循环就无法获知的\(m_N\)，因此我们很难将它们合并起来。

我们可以构造一个\(d_i^{'}=\sum_{j=1}^ie^{x_j-m_i}\)替代原有的\(d_i=\sum_{j=1}^ie^{x_j-m_N}\)以取消其对\(m_N\)的全局依赖，并且只要一达到\(i=N\)，我们自然而然的就有\(d_N^{'}=d_N\)，因此我们可以用\(d_N^{'}\)来替换\((11)\)中的\(d_N\)。并且我们可以求得\(d_{i}^{'}\)和\(d_{i-1}^{'}\)之间的递推关系：

\[d_i^{'}=\sum_{j=1}^ie^{x_j-m_i} =(\sum_{j=1}^{i-1}e^{x_j-m_i})+e^{x_i-m_i}=(\sum_{j=1}^{i-1}e^{x_j-m_{i-1}})e^{m_{i-1}-m_i}+e^{x_i-m_i}=d_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i} \tag{12} \]

可以看到这里的公式依赖于\(m_{i-1}\)和\(m_i\)。因此我们可以把\((9)\)和\((10)\)放进一个循环中：

for i = 1 to N do:

\[m_i\leftarrow max(m_{i-1},x_i) \tag{13} \]

\[d_i^{'} \leftarrow d_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i} \tag{14} \]

end

for i = 1 to N do:

\[a_i \leftarrow \frac{e^{x_i-m_N}}{d_N^{'}} \tag{15} \]

end

这样我们实现了3次循环到2次循环的合并，从而减少了1/3的内存访问。但是我们能否进一步直接合并到一步循环内呢。对于softmax来说，很不幸的是不可能的。但对于我们要求的Attention来说，这是可以实现的。

FlashAttention V1

对于Attention来说，我们最终要获得的并非是softmax后得出的矩阵\(P\)，而是输出矩阵\(O=PV\)，因此我们的目标是尝试找到一个一步循环求得\(O\)​的方法。

我们先来看应用了online softmax的Attention计算过程：

for i = 1 to N do:

\[x_i \leftarrow Q[k,:]K^T[:,i] \]

\[m_i\leftarrow max(m_{i-1},x_i) \]

\[d_i^{'} \leftarrow d_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i} \]

end

for i = 1 to N do:

\[a_i \leftarrow \frac{e^{x_i-m_N}}{d_N^{'}} \tag{16} \]

\[o_i\leftarrow o_{i-1}+a_iV[i,:] \tag{17} \]

end

\[O[k,:]\leftarrow o_N \]

我们将\((17)\)中的\(a_i\)替换成定义式\((16)\)，从而有：

\[o_i=(\sum_{j=1}^i\frac{e^{x_j-m_N}}{d_N^{'}}V[j,:]) \tag{18} \]

这里可以看到依赖于两个全局值\(m_N\)和\(d_N^{'}\)。我们可以应用和online softmax推导时类似的技巧，先构造一个\(o_i^{'}\)：

\[o_i^{'}=(\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i^{'}}V[j,:]) \]

只要达到\(i=N\)，我们就有\(o_N^{'}=o_N\)，并且我们可以求出一个\(o_{i-1}^{'}\)到\(o_i^{'}\)之间的递推公式：

\[o_i^{'}=(\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i^{'}}V[j,:])=(\sum_{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i^{'}}V[j,:])+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:]\\ =(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{'}}\frac{e^{x_j-m_i}}{e^{x_j-m_{i-1}}}\frac{d_{i-1}^{'}}{d_i^{'}}V[j,:])+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:] \\ =(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{'}}V[j,:])\frac{d_{i-1}^{'}}{d_i^{'}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:] \\ = o_{i-1}^{'}\frac{d_{i-1}^{'}}{d_i^{'}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:] \tag{19} \]

可以看到这里不再依赖任何一个全局值，因此我们可以得到Flash Attention的算法：

for i = 1 to N do:

\[x_i \leftarrow Q[k,:]K^T[:,i] \]

\[m_i\leftarrow max(m_{i-1},x_i) \]

\[d_i^{'} \leftarrow d_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i} \]

\[o_i^{'}=o_{i-1}^{'}\frac{d_{i-1}^{'}}{d_i^{'}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:] \]

end

\[O[k,:]\leftarrow o_N^{'} \]

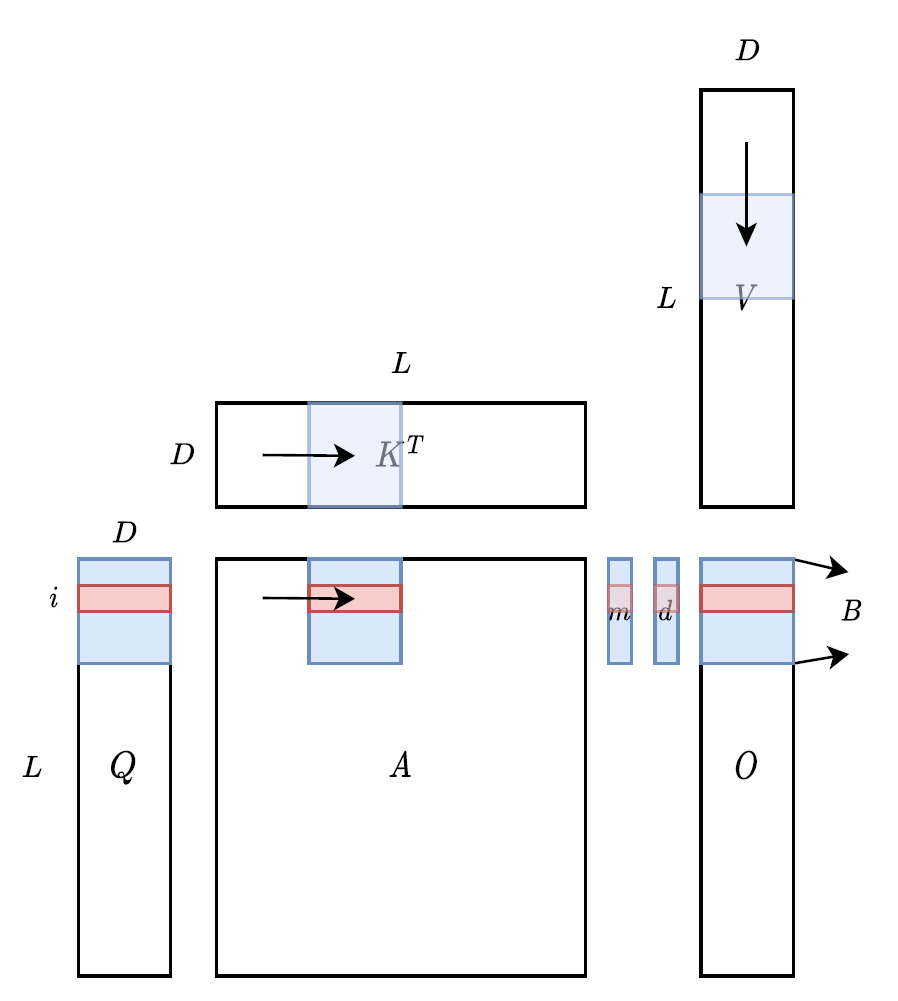
我们可以进一步对这个算法应用分块（tiling），假定tile的大小为\(b\)，共分块\(\#tiles\)个。那么\(x_i\)为存储\([(i-1)b:ib]\)的\(QK^T\)值的向量。\(m_i^{(local)}\)为向量\(x_i\)的局部最大值。那么对于每个tile，有：

for i = 1 to #tiles do:

\[x_i \leftarrow Q[k,:]K^T[:,(i-1)b:ib] \]

\[m_i^{(local)}\leftarrow max_{j=1}^b(x_i[j]) \]

\[m_i \leftarrow max(m_{i-1},m_i^{(local)}) \]

\[d_i^{'} \leftarrow d_{i-1}^{'}e^{m_{i-1}-m_i}+\sum_{j=1}^b e^{x_i[j]-m_i} \]

\[o_i^{'}=o_{i-1}^{'}\frac{d_{i-1}^{'}}{d_i^{'}}e^{m_{i-1}-m_i}+\sum_{j=1}^{b}\frac{e^{x_i[j]-m_i}}{d_i^{'}}V[j+(i-1)b,:] \]

end

\[O[k,:]\leftarrow o_{N/b}^{'} \]

形象的理解如下图所示：

最后我们来看效果，由于\(S\)和\(P\)的计算完全在SRAM上完成（之前做不到的原因在这节开头时说了，想要完整的把\(S\)，\(P\)放上去，片上SRAM的容量不够，但是采用分块迭代策略后就ok了）而不需要对HBM做写回。因此在Standard Attention一节我们分析的，\(O(N^2)\)的\(S\)，\(P\)的HBM读写开销就没有了，只有\(Q\)，\(K\)，\(V\)，\(O\)的\(O(Nd)\)的开销，但我们之前也分析过，由于\(N\gg d\)，所以\(N^2\gg Nd\)，我们可以进一步的当作现在的显存开销变成了只有与\(N\)线性相关，而非二次相关的\(O(N)\)。从\(O(N^2)\)到\(O(N)\)，这显然是一个非常显著的改进。

FlashAttention V2

在V1的基础上，我们来看V2的一个insight。从硬件的角度来说，GPU计算矩阵乘加的算力是远高于其他的运算的。具体来说，以A100为例，FP16/BF16的矩阵乘法可以达到312TFLOPS，但是对于非矩阵乘法的FP32，其算力只有19.5TFLOPS，差了一个数量级（16x）。因此一个明显的改进思路是减少FlashAttention中的非矩阵乘加运算。

观察公式\((19)\)，一个切入点是每个循环计算\(O\)时进行了两次除法，即：

\[o_i^{'}=o_{i-1}^{'}\frac{d_{i-1}^{'}}{d_i^{'}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{'}}V[i,:] \]

两项都需要除以\(d_i^{'}\)。因此相当于是进行了2N次的除法。但实际上这个除法操作可以提取到循环外，即每次更新\(o_i^{'}\)时，采用：

\[\widetilde{o}_i^{'}=\widetilde{o}_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i}V[i,:] \]

因此每次更新时可以只维护未缩放的\(\widetilde{o}_i^{'}\)。当\(i=N\)时，利用\(o_N^{'}=\widetilde{o}_N^{'}/d_N^{'}\)​，可以将之前每次循环中的2N次除法提出，变成循环结束后进行一次除法，从而大大减少除法的计算量（从2N次变为1次）。

即：

for i = 1 to N do:

\[x_i \leftarrow Q[k,:]K^T[:,i] \]

\[m_i\leftarrow max(m_{i-1},x_i) \]

\[d_i^{'} \leftarrow d_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i} \]

\[\widetilde{o}_i^{'}=\widetilde{o}_{i-1}^{'}e^{m_{i-1}-m_i}+e^{x_i-m_i}V[i,:] \]

end

\[o_N^{'}=\frac{\widetilde{o}_N^{'}}{d_N^{'}} \]

\[O[k,:]\leftarrow o_N^{'} \]

最本质的原因其实在于在迭代计算时，实际上每一次\(o_i^{'}\)的缩放项\(d_{i-1}^{'}/d_i^{'}\)都可以把上一次\(o_{i-1}^{'}\)的共分母\(d_{i-1}^{'}\)​给吸收掉。因此也可以在迭代时直接丢弃这个冗余的运算（不妨联想一下反向传播的链式法则，有一定的相似性）。

V2为了应对训练时的需求，在前向计算的循环中也会暂存维护一个变量，不过我们这里不做详细讨论。此外V2在算法上也根据GPU特性更改了内外层循环的顺序来提高并行度，但这里就不去做详细介绍了，可以看论文以及其他的博客理解。

FlashAttention V3

现在来看V3。在V2的基础上，为了提升Flash Attention算法在H100 GPU上的利用率，V3做了几件事，首先将GEMM操作以Producer & Consumer的形式进行了异步化，随后通过Ping-Pong操作将softmax操作隐藏到GEMM操作中（GEMM-softmax流水线），最后应用了更低精度的FP8数制GEMM操作来实现性能提升。

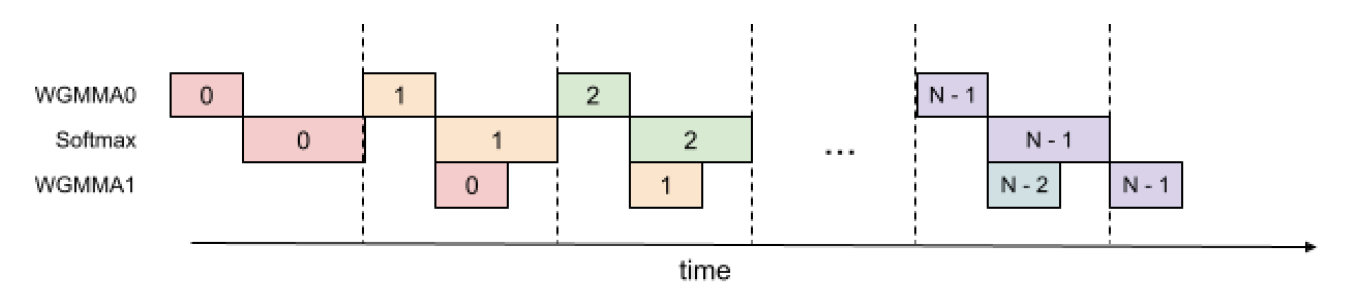
Producer和Consumer的理解其实很简单，Producer的目的是从HBM中加载计算所需的\(Q\)，\(K\)，\(V\)，而Consumer的内容和V2的公式完全一样，主要起到消耗掉Producer提供的\(Q\)，\(K\)，\(V\)并计算\(O\)然后写回。通过Ping-Pong调度这两个部分，可以把慢速的softmax操作隐藏到分段的GEMM操作中。具体来说，以下图为例，当一个Warpgroup在进行GEMM操作时，另一个Warpgroup在进行前一批GEMM操作后的softmax操作中去。

更一步的，在一个Warpgroup中，我们可以将一些softmax的指令与GEMM的指令进行并行来进一步提高吞吐率。如下图所示，可以将一些Softmax的指令隐藏到GEMM的指令执行时间中去。

具体的算法上和V2实际上没有发生什么变化。

参考文献

From Online Softmax to FlashAttention

FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning

FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision