模拟集成电路设计系列博客——8.2.3 振荡器的相位噪声

8.2.3 振荡器的相位噪声

振荡器的相位噪声是一个基本特征。因为不存在一个无损失的振荡器（那就是永动机了），任何振荡器都需要一些有源电路来维持振荡，而这些有源电路会引入噪声。具体哪个器件引入了噪声的机理很微妙，到了后来才逐渐变得易于理解。但是，相位噪声的现象学事实是公认的，并且足以作为集成电路振荡器和PLL的基本认知。

集成电路振荡器的相位噪声可以用下面的公式来建模：

\[S_{phi,osc}(f)=h_0+\frac{h_2}{f^2}+\frac{h_3}{f^3} \tag{8.2.9} \]

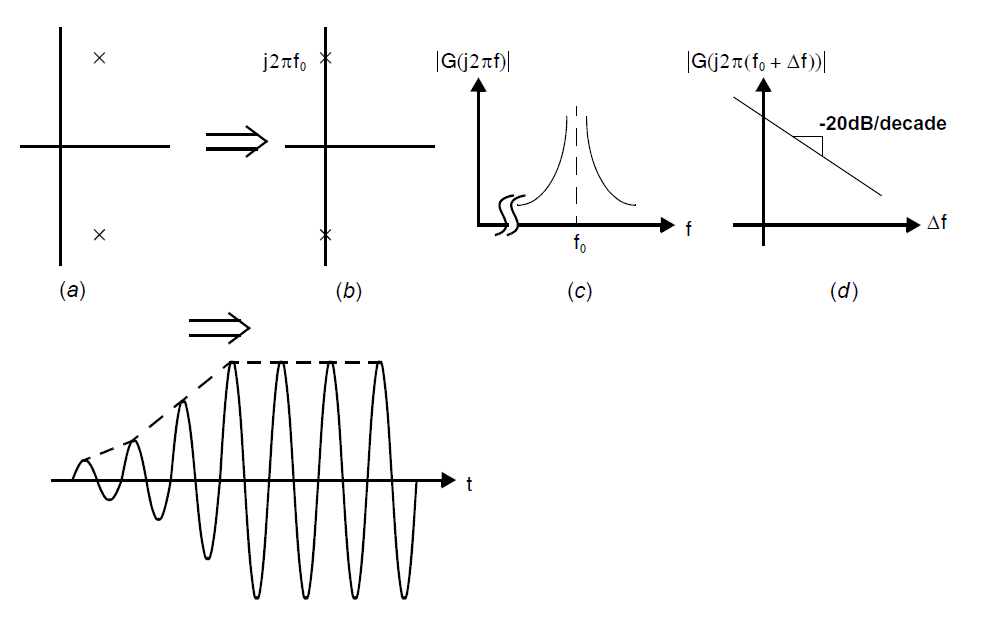
尽管从\((8.2.9)\)中严格推导出为什么包含这三项很困难，但是它们的存在可以通过简单的讨论理解。对环形振荡器和LC振荡器的小信号分析基本上揭示了其极点位于右半平面，如下图中(a)所示，因此其因此其冲激响应为一个指数发散曲线。这些振荡器的幅度最终会饱和。尽管饱和是一个非线性行为，但这个结果类似一个线性系统中极点恰好处于虚轴上的状态，如下图中(b)所示：振荡器保持固定幅度振荡。线性模型的频率响应为\(G(j2\pi(f_0)+\Delta f)\)，小频率偏移\(\Delta f\)大致恒定，极点项除外。

\[G(j2\pi(f_0)+\Delta f)=(\frac{1}{1-j(f_0+\Delta f)/jf_0})\cdot(...)=(\frac{-f_0}{\Delta f})\cdot(...) \tag{8.2.10} \]

振荡器内的噪声通过\(|G(j2\pi(f_0)+\Delta f)|^2\)整形，根据\((8.2.10)\)其与\(1/\Delta f^2\)成正比。我们将\(1/\Delta f^2\)噪声整形记为\(\mathcal{L}(\Delta f)\)，在实践中可以在噪声频谱中观察到这个整形，如下图所示。

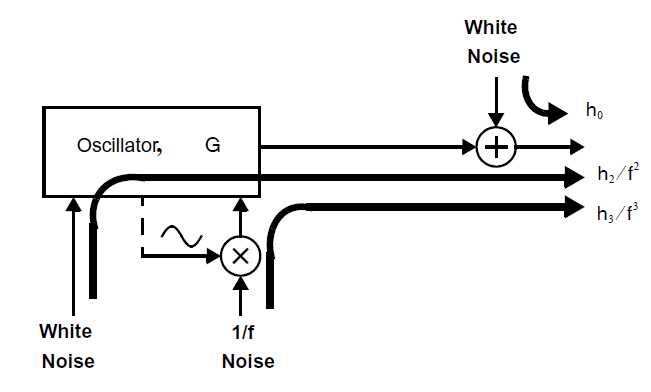
因此，振荡器闭环反馈回路中的噪声被振荡器的响应整形导致了\((8.2.9)\)中的\(h_2/f^2\)。一些一些噪声源在振荡器中开关，导致了其噪声频谱密度在被振荡器响应整形之前上变频。下图展示了一个典型的例子，噪声被一个有着振荡输入的差分对的尾电流源引入。闪烁噪声因此发生了上变频，导致被闭环振荡器响应的整形后产生了\((8.2.9)\)中的\(h_3/f^3\)项。叠加在正弦曲线上的加性白噪声会产生白相位噪声。当白噪声被引入振荡器（例如通过缓冲器）后会发生的情况，产生的相位白噪声可以通过\((8.2.9)\)中的\(h_0\)来建模。

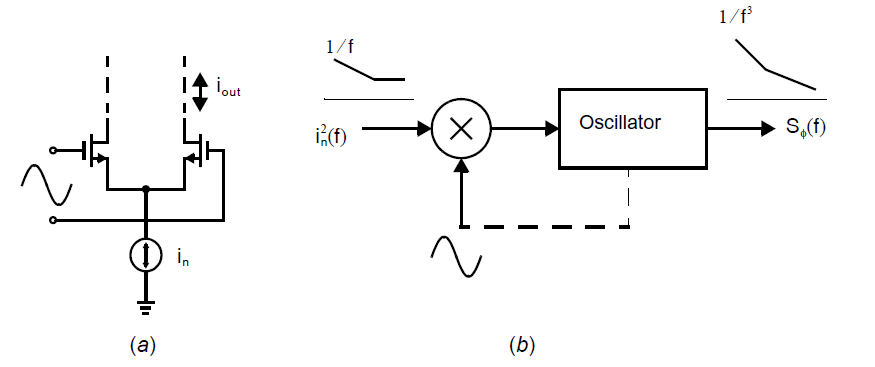
上述三种噪声的来源可以见下图：

\((8.2.9)\)中的相位噪声的对数曲线如下图所示：

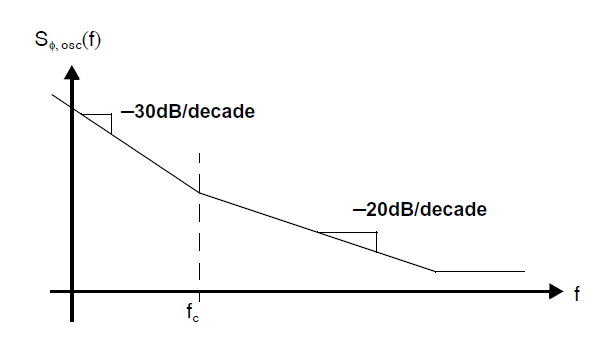
角频率\(f_c\)标记了\(1/f^2\)决定的区域到\(1/f^3\)的区域的转折点，\(f_c\)由这两项对\(S_{\phi}\)贡献相同的频率点决定：

\[f_c=\frac{h_3}{h_2} \tag{8.2.11} \]

一个潜在的应用\((8.2.9)\)做相位噪声建模的麻烦是，闭环噪声项\(1/f^2\)和\(1/f^3\)导致不同的噪声源开始分离。这些具体的噪声我们会在下一章节介绍。由于一个振荡器的绝对抖动确实会发生分离，\((8.2.9)\)的简单相位噪声模型公式在非常小偏移频率\(f\)时是不精确的。问题在于将相位噪声定义为\(\phi_k\)的噪声频谱密度严格的仅仅在相位是平稳随机过程时才能有效。但实际上相位并不是平稳随机过程[Gardner, 2005]。在通过长周期时间的观察（以秒为单位）这种非静态会导致分析问题，所以在只有几赫兹时一般不会考虑相位噪声。在超过这个限制之后，\((8.2.9)\)的相位噪声模型是可靠二点，并且可以积分用于精确的估计抖动。

为了理解一个振荡器的绝对抖动的无界性，考虑P周期抖动在增大P时会发生的变化（P周期抖动指P个周期下实际相位与理想相位的误差）。如下图所示：

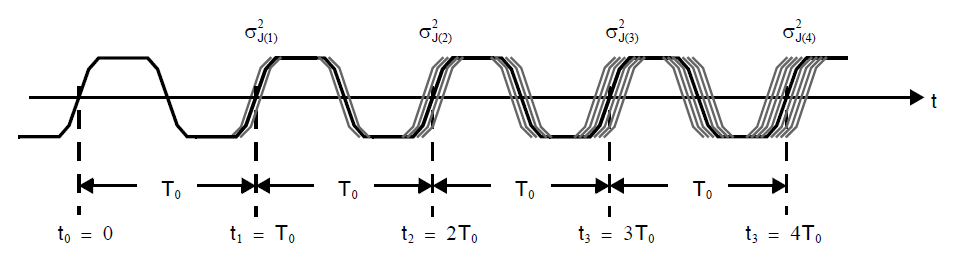
随着P的增大，振荡器第P次过零点时间的方差增大。从定性上讲，这是因为由于内部噪声导致的振荡器状态干扰持续存在，围绕其闭合反馈回路循环。因此，抖动成为过去所有时间的噪声贡献的叠加，并且无限制地增长。随着 P 的增加，积分中包含更多的低频相位噪声，因此产生的 P 周期抖动会增加。如下图所示[Liu, 2004]：

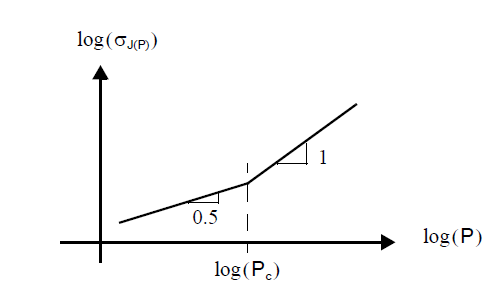
\(h_2/f^2\)的相位噪声分量导致 P 周期抖动与\(\sqrt{P}\)成正比增加，通过公式表达为：

\[\sigma_{J(P)}=\sqrt{h_2T_0^3}\cdot \sqrt{P} \tag{8.2.12} \]

一旦P变得足够大，低于\(f_c\)的频率就会产生显着影响。\(h_3/f^3\)项就会导致 P 周期抖动与\(P\)成正比例增长，两种行为之间的转换点为：

\[P_c\approx \frac{1}{25T_0f_c} \tag{8.2.13} \]

通过上图中的时域测量结果，\((8.2.12)\)和\((8.2.13)\)可以用于估算集成电路振荡器的相位噪声。

例题：

观察不同P在\(1.5 GHz\)下工作的VCO的P周期抖动，以获得如上图所示的曲线，得到\(P_c=30\)。10 个周期 (\(P=10\))的P周期抖动均方根为2.0ps。使用\((8.2.9)\)的模型估计VCO的相位噪声，但忽略白相噪声项，因为该项仅在非常高的频率下才重要。

解答：

将\(P=10\)，\(\sigma_{J(10)}=2ps\)以及\(T_0=(1/1.5\cdot 10^9)\)代入\((8.2.12)\)，可以得到\(h_2\approx 1350 rad^2\cdot Hz\)。使用\((8.2.13)\)，代入\(P_c=30\)得到\(f_c\approx 2MHz\)。随后代入\((8.2.11)\)可以得到\(h_3 \approx 2.7\cdot 10^9 rad^2\cdot Hz^2\)。因此，VCO的相位噪声建模为：

\[S_{\phi,osc}(f)=\frac{1350rad^2\cdot Hz}{f^2}+\frac{2.7 \cdot10^9 rad^2\cdot Hz}{f^3} \tag{8.2.14} \]