模拟集成电路设计系列博客——8.2.1 环形振荡器
8.2.1 环形振荡器
在这一章节,我们将介绍振荡器的基本概念。环路振荡器可以分成若干种,但两种主要的分类依据是直接产生正弦信号还是产生方波(或者三角波)信号输出。正弦波输出振荡器常被用于一些频率选择或者反馈电路的调谐电路,而方波输出振荡器常被用于一个非线性反馈电路例如弛豫振荡器或者环形计数器。使用调谐电路的正弦振荡器可以进一步被分为RC电路,开关电容电路,LC电路与晶体电路。下图展示了振荡器的分类:
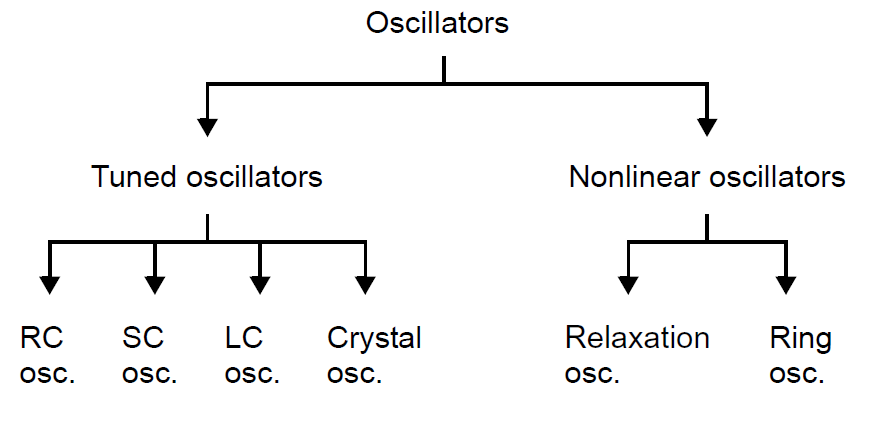
在集成电路中最常用的两种振荡器分别是环形振荡器和LC振荡器。除非在振荡器电路中使用精确的片外元件,否则他们的频率在工艺,温度,以及供电电压偏差下很难做到精确。因此,集成电路振荡器往往会在设计时带有可以修调其工作频率的电路。用于修调的对象一般是振荡器中某些节点的电压,因此这些电路也可以被称为压控振荡器VCO。
接下来我们将首先介绍环形振荡器。最常见的一种实现数字输出MOS VCO的方式就是电压控制的环形振荡器。环形振荡器可以通过奇数个开环反相放大器形成反馈回路来实现。最简单放大器可以就是简单的数字反相器,如下图所示:
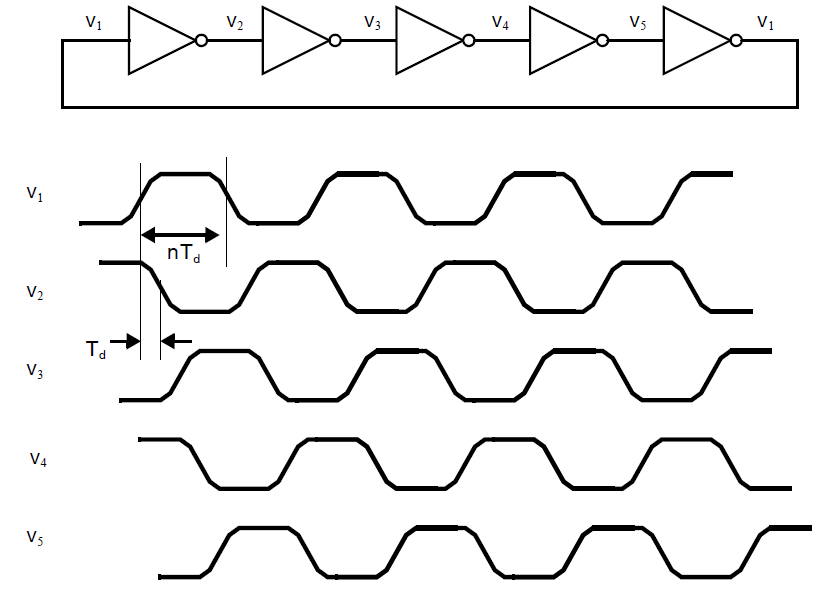
设想在启动时,电路传输中的一些电压从低电压转换成高电压。每半个周期,这个转换会反相围绕整个环路传播。例如,假设第一个反相器的输出变成了1。这个变化会在\(T_0/2\)的时间内传遍五个反相器,此时第一个反相器的输出会变为0;再经过\(T_0/2\)的时间之后,第一个反相器的输出又变回了1,如此反复。假设每个反相器的延迟为\(T_d\),一共有n个反相器,那么半个振荡器周期为:
因此:
上图展示了\(n=5\)的情况。假设反相器的延迟可以用电压控制,那么我们就可以实现VCO。
例题1:
如下图(a)所示的\(n=1\)的反相器环路的行为是?
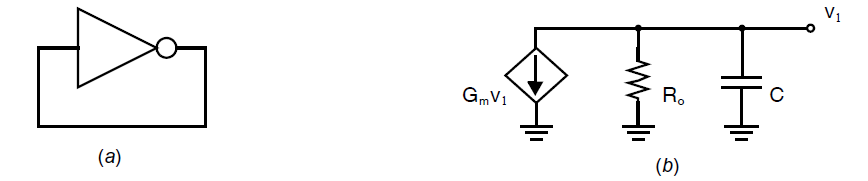
解答:
基于\((8.2.2)\),根据前面的讨论,设计者可以认为这个电路以\(f_0=1/(2T_d)\)频率振荡。但是一个反相器的一阶小信号模型如上图(b)所示,显然是一个无驱动的单时间常数电路,其解为指数衰减:
当反相放大器是一个简单的数字CMOS反相器时,这个分析会很精确并且而且不会发生振荡,在实验中也可以轻易验证。其电压会快速建立到一个地和电源之间的直流值。事实上,这是一个有用的偏置电路,用于产生精确殿宇反相器翻转点的直流电压,其中\(v_{out}=v_{in}\)。
如果反相放大器有其他没有由上图(b)中的小信号原理图表示出的内部节点,那么它将具有一个高阶响应,其分析也会变得更加复杂。
例题1展示了仅仅对环形振荡器做时域分析的缺点。环形振荡器实际上是一个反馈电路,因此为了其能够震荡其应该是不稳定的。假定使用上图(b)中的一阶模型来建模反相器,那么断开环形振荡器任意一点可以得到环路增益:
假定\(G_mR_o>>1\),每个反相器在其单位增益频率点有着接近90°的相移。因此只要有3个或者更多的反相器,就可以保证在相位变得大于180°时环路增益仍然会大于单位增益。但是,在\(n=1\)时,环路在单位增益频率仅仅有90°的相位移动,所以系统仍然稳定。
例题2:
当\(n=2\)时振荡器环路的行为是?
解答:
这是一个双稳定电路,即其具有两个稳定工作点,如下图所示:
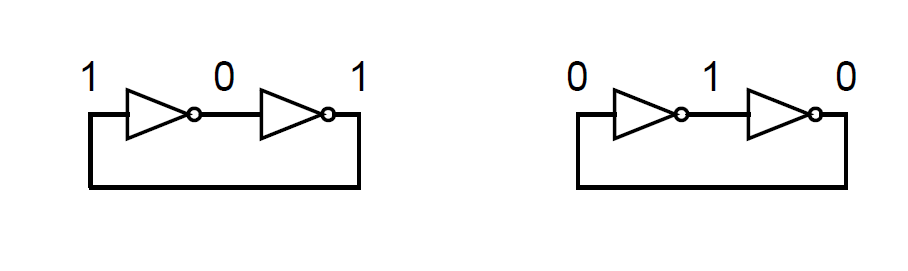
这是基本数字锁存器的理想行为。没有其他的工作点能够稳定,所以一旦启动电路,电路就会建立到两个稳态之一,并且如果不被强制切换到另一个状态下就会保持原有状态。这个电路也不会振荡。
上例中的正反馈环路不稳定但是同样无法震荡。可以将其设想成在直流有着额外180°相移的负反馈环路。因此,节点电压呈现指数发散直到所有级饱和导致环路闩锁。因此,如果使用单端反相器,就需要\(n\)为奇数。
在许多集成环路振荡器中,全差分反相器被用于获得更好的电源电压不敏感性。在使用这种模式时,可以使用偶数个反相器,而环路所需要的反相可以通过将最后一个反相器交叉后再反馈给输入来实现,如下图所示:
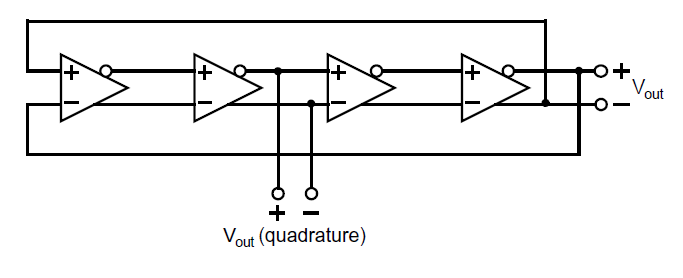
这里有一个非常重要的优点:中间的反相器的输出与最后一个反相器的输出有着一个正交相位的关系(假定所有的反相器以及其负载精确匹配)[Buchwald,1991]。正交输出在许多通信的应用中非常有用,例如正交调制器以及一些时钟提取电路。
一个实现可控延迟的全差分反相器的例子如下图所示:
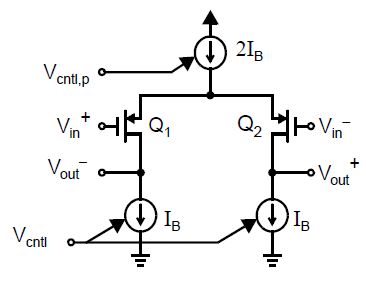
其中电流源负载是可用电压控制的。假定电流源负载正比例于\(V_{cntl}\),比例系数为\(K_{bias}\),我们有:
每个反相器的延迟正比例于反相器的单位增益频率,即:
其中\(C_L\)是反相器的负载电容,\(g_m\)是驱动晶体管的跨导。由于\(g_m\propto \sqrt{I_B}\)。我们你知道延迟正比于\(1/\sqrt{I_B}\propto 1/\sqrt{V_{cntl}}\)。因此,\(f_{osc}\propto \sqrt{V_{cntl}}\) 。所以可以看到振荡器频率与控制电压之间的关系并不是很线性。再PLL中,这个非线性意味着\(K_{osc}\)是\(f_{osc}\)的函数,环路带宽与建立时间同理。这个非线性的主要原因是在更高的频率时,每一级的电压改变的幅度由于\(I_B\)的增加而增加。
如果设计者可以确保延时单元的电压改变独立于振荡器频率,那么就可以实现一个有着良好的电压-频率线性度的环形振荡器VCO[Kim, 1990; Young, 1992; Reynolds, 1994]。一个实现了线性化的差分延迟级,以及用于控制电压摆幅的偏置电路如下图所示[Young, 1992]:
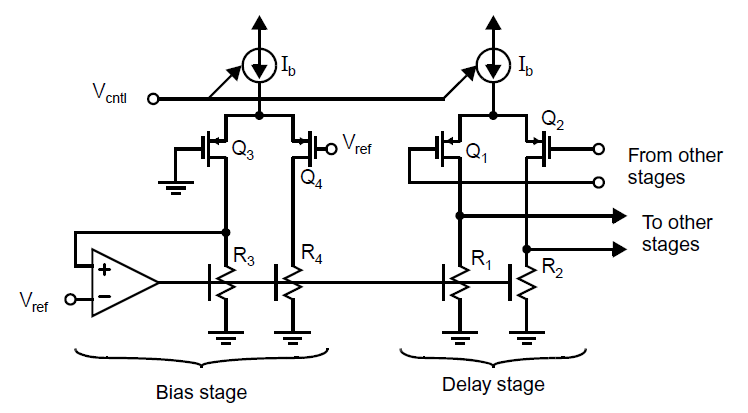
每一级由一个p沟道输入晶体管的差分放大器以及电阻负载组成。电阻负载通过偏置在线性区的n沟道晶体管实现。其阻抗通过偏置电路调节,从而使得所有的\(I_b\)流经其时,其两侧会有\(V_{ref}\)的电压,\(V_{ref}\)则通过一个温度无关的电压基准提供。这可以通过将一个延迟单元复制到偏置电路来实现。这个复制过来的电路由\(Q_3\),\(Q_4\),\(R_3\)和\(R_4\)组成,这个电路中所有的\(I_b\)流经\(Q_3\)和\(R_3\),所以\(Q_4\)和\(R_4\)实际上可以从电路中去除。回忆\(R_3\)实际上是通过n沟道晶体管实现,可以看到包含放大器的负反馈循环会使得\(I_b\)流经时\(R_3\)两端的电压为\(V_{ref}\)。由于放大器的输出也被用于控制所有环形振荡器的延迟单元的线性区晶体管的阻抗,它们也会在\(I_b\)流经时两端电压为\(V_{ref}\)。接下来,如果VCO由于\(V_{cntl}\)的变化而发生频率改变,进而导致\(I_b\)改变,环路会改变所有延迟级的负载,从而使通过其的最大电压仍然为\(V_{ref}\)。假定每一级的电容负载为常数,那么每级的延迟就会与\(I_b\)呈反比,意味着频率与\(I_b\)呈正比。
环形振荡器的一个有趣的改动方式如下图所示:
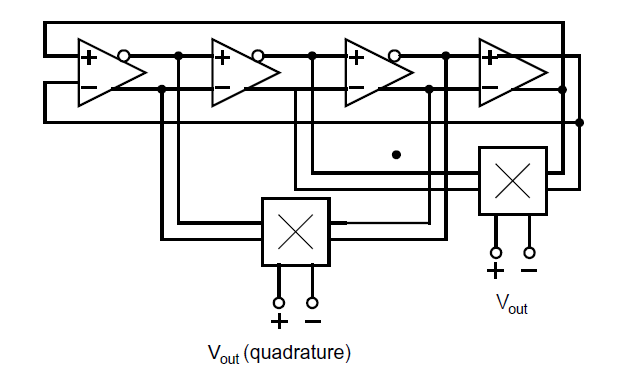
相比最初的差分反相器环形振荡器结构增加了两个乘法器,这个修改可以将输出频率放大一倍,且仍然实现两个正交输出[Buchwald, 1992]。事实上,如果不需要正交输出,那么可以直接将两个乘法器的输出连接到一个额外的第三个乘法器上,这样也可以加倍频率,只是就只有单独一个输出。另一个有趣的变种是[Razavi, 1994],一个三级振荡器的输出被一一个新颖的方式组合来获得一个单端输出,其周期只相当于两个反相器延迟。


