模拟集成电路设计系列博客——8.1.2 锁相环的基本组件
8.1.2 锁相环的基本组件
-
压控振荡器(VCO):PLL的一个关键组件是VCO,一个有着震荡输出的电路(以正弦波或者其他的时钟信号的形式),其频率取决于输入的控制电压\(V_{cntl}\)。因此,假定VCO的输出为随着时间缓慢变化的正弦电压,其可以通过下面的方程表示:
\[V_{osc}(t)=Esin[\omega_0t+\phi(t)] \tag{8.1.1} \]其中\(\omega_0\)为振荡器的标称频率或者自由运行频率,而振荡器的瞬间相位为\(\phi_t\)。这个振荡器的瞬间频率为\([\omega_0t+\phi(t)]\)在\(rad/sec\)单位下的改变速率:
\[\omega_{inst}(t)=\frac{d[\omega_0t+\phi(t)]}{dt}=\omega_0+\frac{d\phi(t)}{dt} \tag{8.1.2} \]因此,如果振荡器相位\(\phi(t)\)固定,那么瞬间频率就和自由运行频率一致,即\(\omega_{inst}(t)=\omega_0\)。
现在定义VCO的瞬间频率与其自由运行频率之差:
\[\omega(t)=\omega_{inst}(t)-\omega_0 \tag{8.1.3} \]当然,\(\omega(t)\)取决于VCO控制电压\(V_{cntl}(t)\)。根据\((8.1.2)\),\(\omega(t)\)与相位的微分线性相关:
\[\omega(t)=\frac{d\phi(t)}{dt} \tag{8.1.4} \]如果我们对公式两侧做积分,有:
\[\phi(t)=\phi(0)+\int_0^t\omega(\tau)d\tau \tag{8.1.5} \]我们可以看到瞬间相位是瞬间频率微分的积分,对\((8.1.5)\)两侧做拉普拉斯变换:
\[\phi(s)=\frac{\omega(s)}{s} \tag{8.1.6} \]其中\(\phi(s)\)和\(\omega(s)\)是\(\phi(t)\)和\(\omega(t)\)各自的拉普拉斯变换。上面的公式可以用于建模VCO的输入控制电压和其输出信号相位的关系。为了取得一个线性模型,我们假设\(\omega(t)\)正比例于控制电压,比例系数为常数\(K_{osc}\),其单位为\(rad/(sec\cdot V)\):
\[\omega(t)=K_{osc}V_{cntl}(t) \tag{8.1.7} \]即使关系是非线性的,这个公式仍然可以被用于小信号模型,其中\(K_{osc}\)为\(V_{cntl}\)发生小改变时引发\(\omega(t)\)改变的系数。
-
分频器:一个分频系数为\(N\)的理想时钟分频器的功能是产生一个周期性输出,其周期为输入周期精确的\(N\)倍。下图展示了一个\(N=4\)的情况:
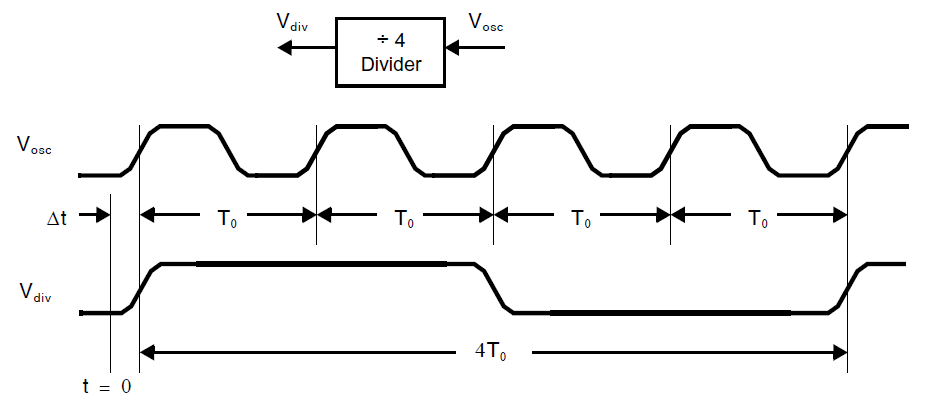
其结果为分频器的瞬时输出频率恰好为输入的\((1/N)\),在PLL中,其输入为VCO的输出。更进一步的,分频器的输出相位\(\phi_{div}(t)\)也恰好是输入\(\phi(t)\)的\((1/N)\)。为了理解这个,注意VCO输出\(V_{osc}\)的相位是时钟的上升沿与一些参考时间的延迟\(\Delta t\),\(t=0\),归一化到周期\(T_0\):
\[\phi = 2\pi \frac{\Delta t}{T_0} \tag{8.1.8} \]假定分频器输出与VCO的输出同步,其相位由相同的延时\(\Delta t\)决定,但是归一化到更长的周期\(NT_0\):
\[\phi_{div}=2\pi \frac{\Delta t}{NT_0}=\frac{\phi}{N} \tag{8.1.9} \]上面的公式提供了分频器的线性模型,两边做拉普拉斯变换后有:
\[\phi_{div}(s)=\frac{\phi(s)}{N} \tag{8.1.10} \] -
鉴相器:鉴相器的作用是产生一个平均值正比例于参考输入相位\(\theta_{in}\)和反馈时钟信号\(\theta_{div}\)的输出信号。类似于在反馈放大器的输入端做的减法。鉴相器有很多种实现形式:一个简单的异或门,一个采样保持电路,一个模拟乘法器,或者一系列数字电路的组合,例如D触发器。所有接收两个时钟信号作为输入,产生一个均值能够提供所需相位信息的输出的电路都可以。
例题1:
模拟乘法器鉴相器的增益为?
解答:
在这个例子中,假定输入信号\(V_{in}\)为一个已知幅度的正弦波。鉴相器通过模拟乘法器来实现,其关系式为:
\[V_{pd}=K_MV_{in}V_{div} \tag{8.1.11} \]其中\(V_{div}\)为分频器输出,\(V_{pd}\)为鉴相器输出,\(K_M\)为乘法器常数,我们假定输入信号的描述为:
\[V_{in}=E_{in}sin(\omega t) \tag{8.1.12} \]分频器的输出同样也是正弦波:
\[V_{div}=E_{div}sin(\omega_t-\phi_d+90°)=E_{div}cos(\omega t-\phi_d) \tag{8.1.13} \]参数\(\phi_d\)表示输入信号与振荡器输出的相位差,之所以有90°的相位差是因为这样在\(\phi_d=0\)时鉴相器的平均输出为零(在这个例子中是模拟乘法器)。模拟乘法器后跟随一个低通滤波器通常被称作模拟上的相关函数。但输入信号和VCO输出有着90°相位差时(\(\phi_d=0\)),他们是非相关的,低通滤波器的输出为零。通过这个90°的相位偏移,如果相位差发生了改变,那么两个波形会产生更大的相位关联(例如\(\phi_d>0\)),相关性增大,随后低通滤波器的输出为正。例如,如果\(\phi_d=90°\),那么振荡器的输出和输入信号恰好同相,鉴相器的输出的平均恰好是两个正弦波之积除以二,因此:
\[V_{cntl}=K_{lp}K_M\frac{E_{in}E_{div}}{2} \tag{8.1.14} \]下图展示了当\(\phi_d\)取得略小于90°时的情况,虚线为两个输入,实线为乘法器输出\(V_{pd}\):
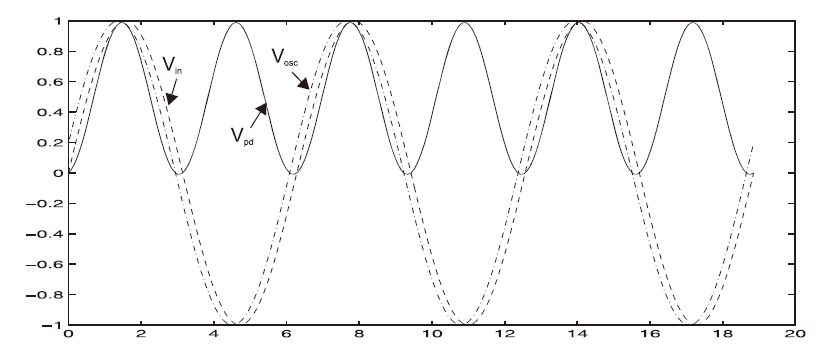
对于\(E_{in}=E_{div}=1V\),以及\(K_M=1V^{-1}\)的情况。此处我们可以看到输出为输入信号的两倍频率,其偏移电压大约为\(1/2V\),这也是低通滤波器可能的最大输出。在另一方面,如果相位改变使得两个波形的相位差更大,那么他们之间的相关度以及滤波器的输出都会为负,如下图所示,展示了不同波形的例子:
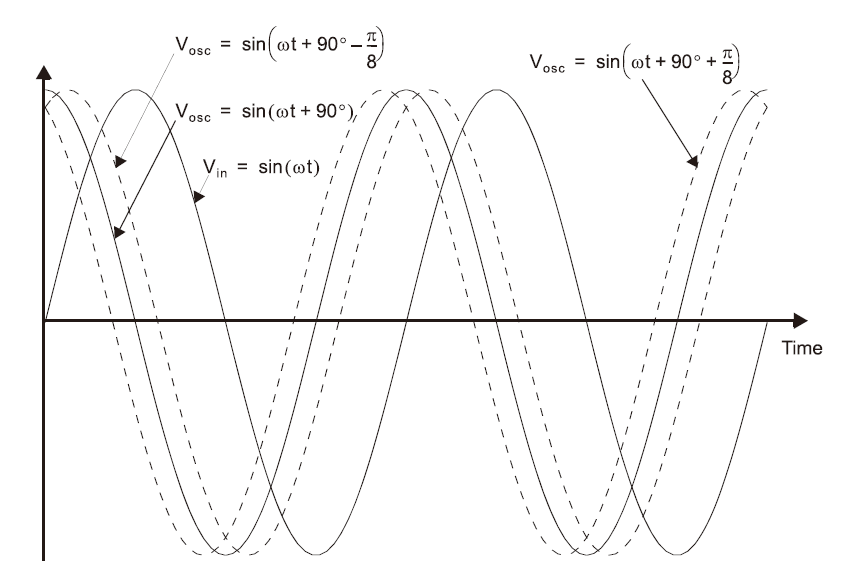
可以看到\(\phi_d>0\)对应更多共相位的波形。
上面的表述可以进行量化,鉴相器的输出为:
\[V_{pd}=K_MV_{in}V_{div}=K_ME_{in}E_{div}sin(\omega t)cos(\omega t-\phi_d) \tag{8.1.15} \]使用三角积化和差公式:
\[sin(A)cos(B)=\frac{1}{2}[sin(A+B)+sin(A-B)] \tag{8.1.16} \]我们有:
\[V_{pd}=K_M\frac{E_{in}E_{div}}{2}[sin(\phi_d)+sin(2\omega t-\phi_d)] \tag{8.1.17} \]低通滤波器会滤除第二项这个两倍于输入信号频率的分量,以你信号\(V_{cntl}\)为:
\[V_{cntl}=K_M\frac{E_{in}E_{div}}{2}sin(\phi_d) \tag{8.1.18} \]注意\(V_{cntl}\)可能是一个直流量,也有可能是一个缓变信号,如果假定输入信号的频率固定或者缓慢改变。对于小的\(\phi_d\),我们可以采取近似:
\[V_{cntl}\approx K_M\frac{E_{in}E_{div}}{2}\phi_d=K_{lp}K_{pd}\phi_d \tag{8.1.19} \]因此低通滤波器的输出近似正比例于振荡器输出和输入信号的相位差,这个近似可以用于分析PLL的线性模型,比例常数\(K_{pd}\)为:
\[K_{pd}=K_M\frac{E_{in}E_{div}}{2} \tag{8.1.20} \]注意模拟乘法鉴相器中,\(K_{pd}\)是一个输入信号幅度与乘法器输出信号幅度的函数。后面我们会知道\(K_{pd}\)会影响环路动态性能,因此我们需要\(E_{in}\)和\(E_{div}\)提前已知。
鉴相器的输出可能是上面例题1中的电压,但在CMOS电路中更常见的是电流,可能是单端也可能是差分。当输出为电流时,定义均值为\(I_{pd}\),鉴相器的增益常数\(K_{pd}\)的单位为\(A/rad\):
\[I_{pd}=K_{pd}\phi_d=K_{pd}(\phi_{in}-\phi_{div}) \tag{8.1.21} \]例题2:
一个电荷泵鉴相器如下图所示:
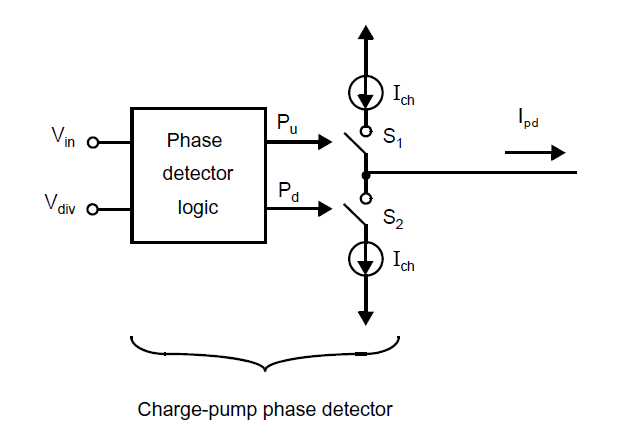
相位检测逻辑的设计原理是当参考时钟领先于反馈时钟,\(\phi_d>0\)时,高逻辑电平产生\(P_u\),如果参考时钟落后,\(\phi_d<0\)时,高电平产生在\(P_d\)。一个典型的逻辑实现如下图所示,试求该鉴相器的增益\(K_{pd}\)。
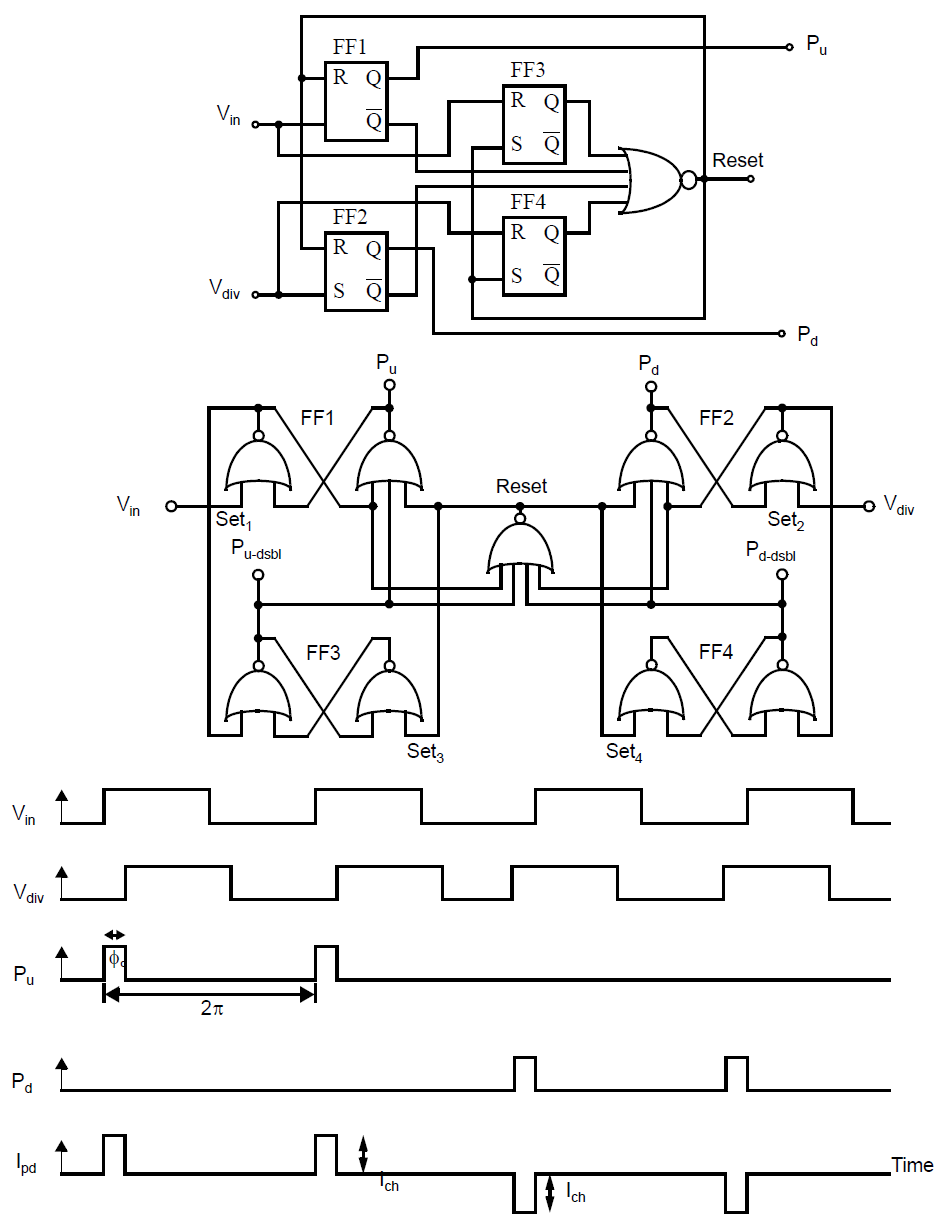
解答:
相位比较器决定进入低通滤波器的是源电流还是沉电流,取决于序列相位检测逻辑的输出。当\(S_1\)闭合,\(I_{ch}\)流入低通滤波器,当\(S_2\)闭合,\(I_{ch}\)流出低通滤波器。序列相位检测逻辑产生两个输出\(P_u\)和\(P_d\),取决于其输入\(V_{in}\)和\(V_{div}\)。其一般是来自PLL输入和VCO的数字信号。尽管有很多种可能的序列相位检测逻辑的实现方式,设计者要考虑的是通过\(V_{in}\)和\(V_{osc}\)的边沿领先控制的电路。如果\(V_{in}\)先于\(V_{osc}\)升高,那么\(P_u\)会在信号不同时升高。这回向环路滤波器中注入电荷来加速VCO。类似的,如果\(V_{osc}\)先于\(V_{in}\)降低,那么\(P_d\)会在输入不同时升高,\(S_2\)闭合,电荷会从环路滤波器中流出,从而降低VCO频率。当边沿一致时,两个输入相位对齐,\(P_u\)和\(P_d\)可能会在数个门延迟时间内升高,但是这个时间足够短,因此其对环路滤波器的输出几乎没有影响,并且这种毛刺会被环路滤波器中的电容显著消除。\(V_{in}\)和\(V_{osc}\)的下降沿对于\(P_u\)和\(P_d\)没有影响,此时两者均为零。这会使得PLL对波形的占空比并不敏感。典型的波形如上图所示。
为了求得鉴相器增益,注意在每个参考时钟\(V_{in}\)的单个周期中被平均的输出电流\(I_{pd}\)是由一个周期中鉴相器\(P_u\)和\(P_d\)所占的周期比例对电荷泵电流\(I_{ch}\)进行缩放获得的:
\[\overline{I_{pd}}=I_{ch}\frac{\phi_d}{2\pi} \tag{8.1.22} \]因此结合\((8.1.22)\)和\((8.1.21)\),我们有:
\[K_{pd}=\frac{I_{ch}}{2\pi} \tag{8.1.23} \] -
环路滤波器:环路滤波器在PLL中起到数个关键作用。其对鉴相器快速变化的输出进行平均。我们也会看到通过决定VCO的输入\(V_{cntl}\)如何对\(I_{pd}\)表示的相位差进行响应,环路滤波器可以决定PLL的环路动态响应。
在大部分PLL中,环路滤波器是一阶或者二阶的。例如,一个常见的一阶低通环路滤波器的传输函数为:
\[K_{lp}H_{lp}(s)=K_{lp}\frac{1+s/\omega_z}{s}=K_{lp}(\frac{1}{s}+\frac{1}{\omega_z}) \tag{8.1.24} \]上面公式中的环路滤波器可以被认为是由比例路径和积分路径组成的。大部分的环路滤波器会引入额外的高阶零极点,但是最关键的PLL设计参数可以通过这个公式获得。
当鉴相器输出为电流时,环路滤波器的增益参数\(K_{lp}\)的单位是\(\Omega\cdot rad/s=F^{-1}\),如果是电压则单位为\(rad/s\)。
例题3:
求取下图中\(I_{pd}\)到控制电压\(V_{cntl}\)的传输函数:
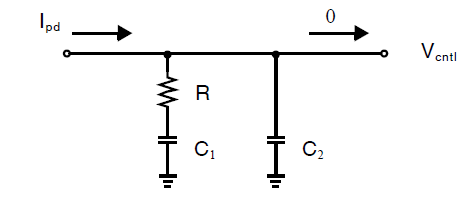
解答:
假定没有电流从环路滤波器流出到VCO的控制端,那么如上图所示,此处可以比认为是两个并联阻抗\(R+1/(sC_1)\)和\(1/(sC_2)\),环路传输函数为:
\[K_{lp}H_{lp}(s)=\frac{V_{cntl}(s)}{I_{pd}(s)}=\frac{1}{s(C_1+C_2)}\frac{1+sRC_1}{1+sR[C_1C_2/(C_1+C_2)]} \tag{8.1.25} \]在实践中,电容\(C_2\)只起到过滤电压脉冲的作用,否则会在\(R\)上出现瞬态电流,因此其值远小于\(C_1\)。假定\((C_1+C_2)\approx C_1\),并且忽略掉\((C_1+C_2)/(RC_1C_2)\)处的高频极点。
\[K_{lp}H_{lp}(s)=\frac{V_{cntl}(s)}{I_{pd}(s)}\approx\frac{1}{C_1}(\frac{1+sRC_1}{s}) \tag{8.1.26} \]将其代入\((8.1.24)\),我们有:
\[K_{lp}=1/C_1 \tag{8.1.27} \]\[\omega_z=1/(RC_1) \tag{8.1.28} \]例子中的环路滤波器常常和上面介绍的电荷泵相位比较器组合使用。当\(S_1\)闭合,\(I_{ch}\)流入低通滤波器,增大VCO的控制电压;当\(S_2\)闭合,\(I_{ch}\)流出低通滤波器,降低VCO的控制电压。当两个开关都断开时,\(C_1\)和\(C_2\)的顶极板都开路,输出电压保持在稳定状态。电阻\(R\)是为了在低通滤波器中引入一个零点。在电容对电流积分时,其提供了一个正比例于输入电流的输出分量。由于两者串联,因此\(V_{cntl}\)上可以看到比例项和积分项。
-
环路小信号分析:PLL的动态特性是设计者常常关注的一个点,具体来说:环路是否稳定?当其离开锁相点时如何稳定?环路内部的噪声如何传递到其输出?如何设计环路来得到一个确定的动态响应?就像反馈放大器一样,线性分析是一个有效的回答上述问题的工具。但是,PLL是一个高度非线性的系统。幸运的是,一旦PLL锁定,其对输入相位的动态响应以及频率变化可以看作近似的线性模型,只有这些改变对于他们的操作点或者偏置点够慢够小。
使用上面描述的关系式,我们可以得到一个PLL的线性模型。需要注意的是这是一个小信号模型,其描述的是在一个工作点上的相对变化。换而言之,相位变量表示的是相对参考信号的相位变化。类似的,任何频率变量也都表示的是相对原始频率的变化。线性化小信号模型的信号流图如下图所示:
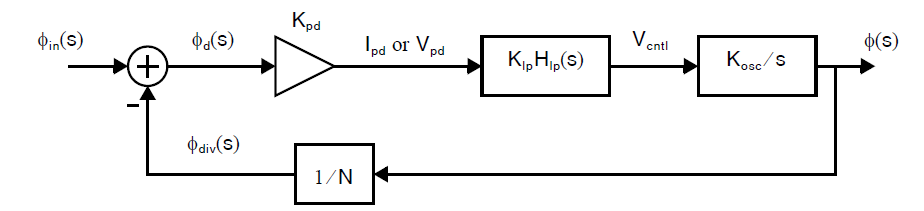
现在我们可以开始对上图中的信号流图进行分析从而得到小信号的传输函数。例如,直接做反馈分析可以知道,关于输入相位\(\phi(s)\)和相位差\(\phi_d(s)\)的传输函数为:
\[\frac{\phi_d(s)}{\phi_{in}(s)}=\frac{1}{1+L(s)} \tag{8.1.29} \]其中\(L(s)\)为环路增益:
\[L(s)=\frac{K_{pd}K_{lp}K_{osc}H_{lp}(s)}{Ns} \tag{8.1.30} \]将\((8.1.30)\)代入\((8.1.29)\)有:
\[\frac{\phi_d(s)}{\phi_{in}(s)}=\frac{s}{s+K_{pd}K_{lp}K_{osc}H_{lp}(s)/N} \tag{8.1.31} \]这个公式很通用,几乎可以用于所有的PLL。PLL之间的差异主要在使用了什么环路滤波器(决定\(H_{lp}(s)\)),鉴相器(决定\(K_{pd}\)),以及振荡器(决定\(K_{osc}\))。


