模拟集成电路设计系列博客——7.5.5 折叠型ADC

7.5.5 折叠型ADC

我们刚了解完输入放大器的数量如何通过插值型架构来减少。但是对于一个N bit的ADC来说，仍然需要\(2^N\)个锁存比较器。这个大量的比较器数量可以通过折叠型ADC架构来减少。折叠型ADC架构类似于两步型ADC，一组LSB分离于一组MSB进行独立的查找。但是，相比两步型ADC需要一个精确的DAC，折叠型ADC通过模拟预处理可以更直接的确定LSB，同时MSB也可以同时确定。

例如，考虑如下图所示的4 bit折叠型ADC。定义折叠率为对于\(V_{in}\)扫描于其输入范围时单个折叠块的输出转换次数，我们可以看到此处的折叠率为4。折叠率决定了MSB转换器需要多少比特。

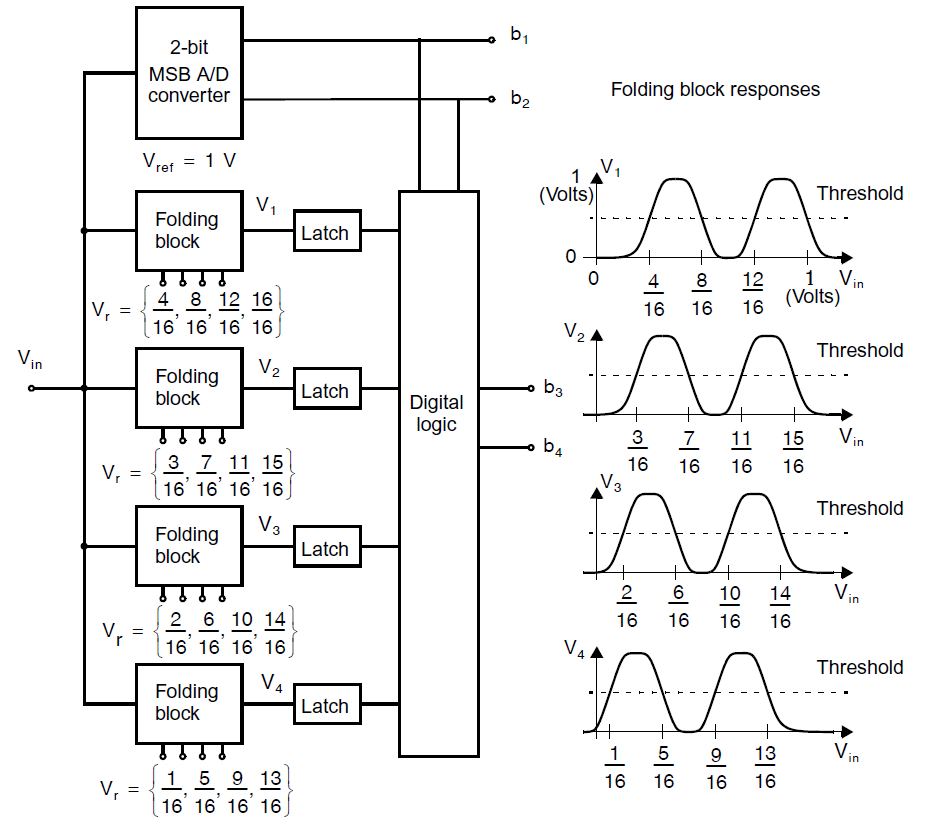
这个ADC的工作流程如下：MSB ADC决定了决定了输入信号在四个输入区间中的哪一个（0到\(1/4\)，\(1/4\)到\(1/2\)，\(1/2\)到\(3/4\)，\(3/4\)到1）。及暖MSB ADC看上去是独立的，但这些需要在折叠块内与合适的信号组合来决定。为了确定两位LSB，\(V_1\)到\(V_4\)在四个MSB区间内都会产生一个温度计码。注意，四个LSB锁存器也被用于不同的MSB区间，当\(V_{in}\)处于\(1/4\)到\(1/2\)或\(3/4\)到1时，温度计码会被取反。例如，随着\(V_{in}\)从0增加到\(1/4\)，温度计码依次为：0000，0001，0011，0111，1111.但是，随着\(V_{in}\)继续增加到\(1/2\)，温度计码依次为1110，1100，1000，0000。同时，注意锁存比较器可以直接用于确定LSB，因为转换点都被折叠块进行了放大。总体来说，相比Flash ADC，折叠降低了锁存比较器的数量。例如，在4 bit转换器中，Flash ADC需要16个锁存器，而折叠型ADC只需要8个。具体来说，4个锁存器被用于MSB ADC，而其他的则如杀个图所示。并且推而广之，实际上锁存器可以得到进一步的节省。

折叠块可以通过交叉耦合差分对来实现，下图展示了一个简化的双极型电路，此处四组差分对晶体管通过如是连接形成下图(b)中的输入-输出响应曲线。输出信号\(V_{out}\)对电压\(V_a\)和\(V_b\)形成了一个或逻辑。换而言之，如果\(V_a\)和\(V_b\)均为低，那么\(V_{out}\)为低，否则\(V_{out}\)为高。关于\(V_a\)和\(V_b\)的行为，当\(V_{in}\)小于\(V_{r3}\)或者大于\(V_{r4}\)时\(V_b\)为低；而\(V_{in}\)大于\(V_{r2}\)或者小于\(V_{r1}\)时\(V_a\)为低。同时，相邻差分对的交叉耦合会使得\(V_{in}\)在\(V_{r1}\)和\(V_{r2}\)之间时\(V_a\)升高，\(V_{in}\)处于\(V_{r3}\)和\(V_{r4}\)之间时\(V_b\)身高。\(V_a\)和\(V_b\)的升高行为可以产生\(V_{out}\)的折叠输出。

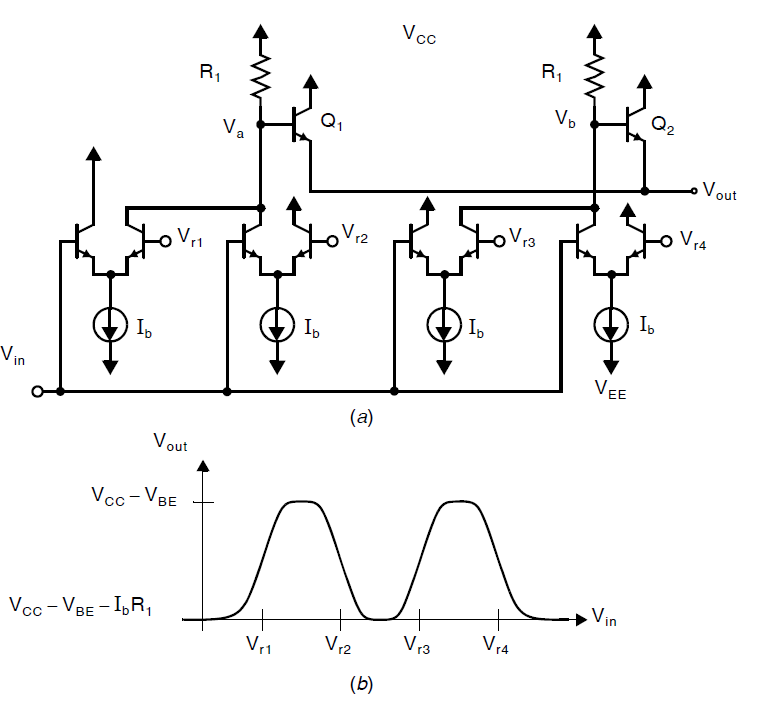
一些值得说明的问题是，对于全范围输入信号，折叠块的输出信号的频率是远高于输入信号的。事实上，折叠块的输出频率等于输入信号频率与折叠率的乘积。这个乘法关系限制了高速ADC中实际折叠率的使用。同时，尽管这里展示的是一个单端电路，但在实际应用中基本上都使用的是差分电路。

另一个值得一提的点是，尽管折叠架构降低了锁存比较器的数量，在Flash ADC中出现的大输入电容问题仍然会出现在上面展示的折叠型ADC中。事实上，Flash ADC的每个比较器有着相似的差分对晶体管输入级，只不过它们不是交叉耦合的。由于每个折叠块中的差分对的数量等于折叠率，且输入信号需要输入到每个差分对的一侧，可以看到输入信号要驱动的晶体管数量等于\(2^N\)，和Flash ADC相同。为了减小这个巨大的输入电容，折叠型ADC也需要利用插值架构。通过对上面的4 bit例子使用二插值技术，我们可以得到下面的架构图：

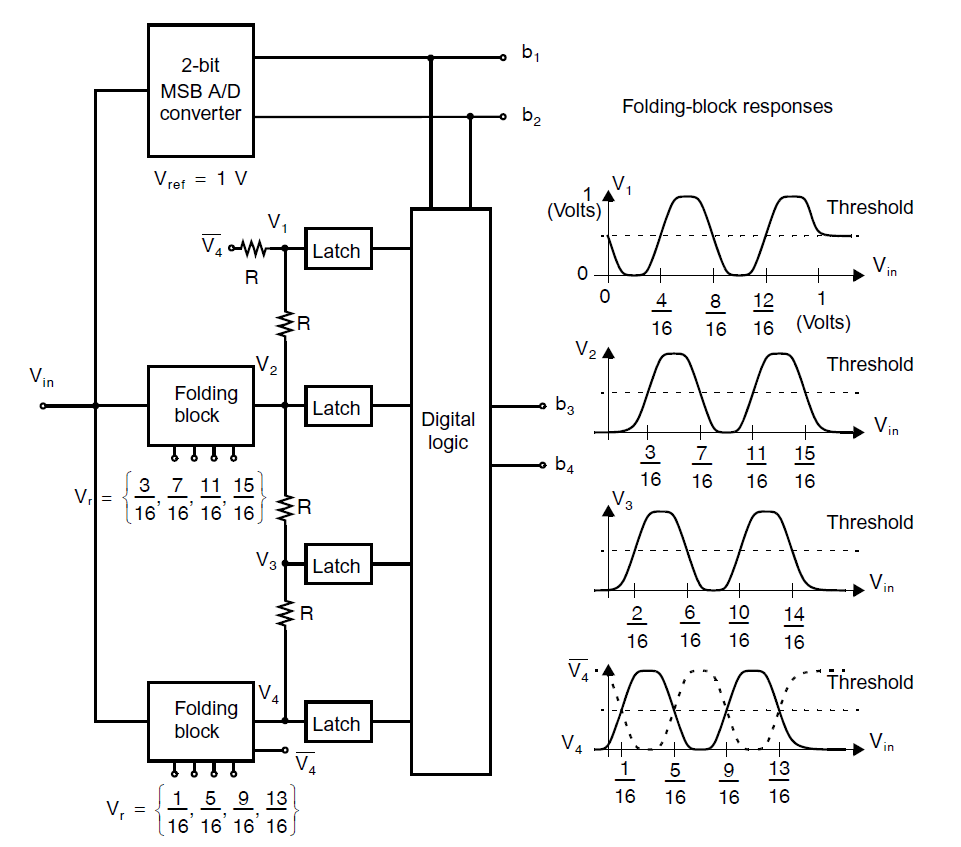
注意一个新的反相信号\(\bar{V_4}\)需要连接顶部折叠块和底部折叠块。对于单端版本电路需要加入这个反相信号，但是在全差分版本中并不需要额外的电路，因为可以通过简单的交叉耦合差分输出线来实现。

在[van Valburg, 1992]中，为了实现了一个非常高速的8 bit ADC，使用了四个折叠块，每个使用了8的折叠率。假定\(V_{ref}=1V\)，那么一个折叠块内相邻参考电压输入的差值为\(1/8V\)。每个相邻的折叠块偏移了\(1/32V\)，使得每过\(1/32V\)就会触发一次过零点。通过在相邻的折叠块之间使用四个8头电阻串，可以实现每\(1/256V\)的过零点（一个有着32个锁存比较器的8 bit转换器连接到插值电阻串）。MSB通过从选定的差分对中选择合适的输出，并将其独立相加来实现额外的折叠放大器，而不进一步增大折叠率。这个ADC同时也包含了防止冒泡错误的电路。另一些折叠型ADC的例子是[van de Grift, 1987; Colleran, 1993]。此外，折叠型ADC已经被用于两步型ADC的中间环节[Vorenkamp, 1992]。

例题：

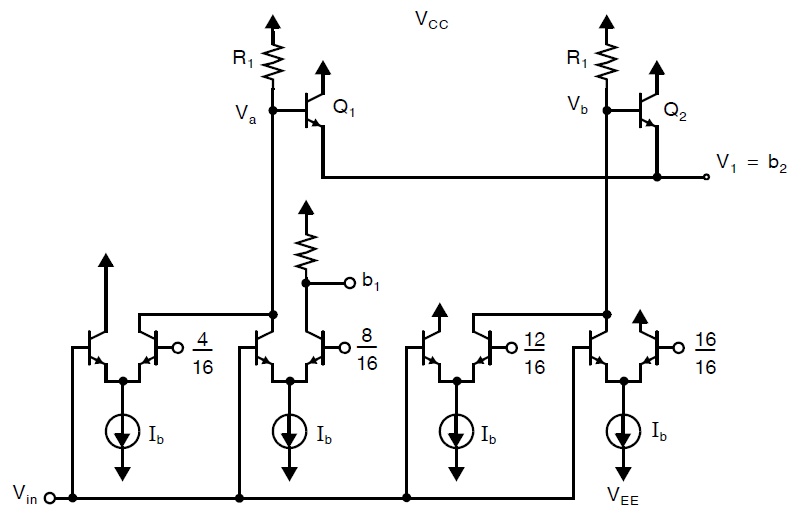
假设使用本节最开始提出的折叠型ADC架构，研究两位MSB如何使用折叠块内部的信号进行驱动。

解答：

MSB中的\(b_1\)通过判断输入信号是否高于或低于\(V_{ref}/2\)来确定。我们可以看到在顶部折叠块中，输入信号与合适的电压\((8/16) V_{ref}\)进行了比较，从而产生\(V_1\)。因此我们可以在顶部折叠块中，直接通过连接到\(V_{r2}\)的晶体管的集极电流来获得MSB。类似的，顶部折叠块使用了\(4/16\)和\(12/16\)的参考，可以用于确定第二个比特\(b_2\)。事实上，信号\(V_1\)可以直接用于确定第二个比特\(b_2\)。因此，两位MSB的\(b_1\)和\(b_2\)可以直接通过折叠块来确定，电路如下图所示：