模拟集成电路设计系列博客——7.5.3 两步型ADC
7.5.3 两步型ADC
两步型ADC常被用于高速中精度的ADC。他们相比Flash ADC能够提供一些额外的优点。具体来说，两步型ADC需要更少的硅面积，消耗更少的能量，有着更小的电容负载，并且比较器需要分辨的电压相比Flash ADC更宽松。两步型ADC的吞吐率可以接近Flash ADC，尽管他们会有着更大的延迟。
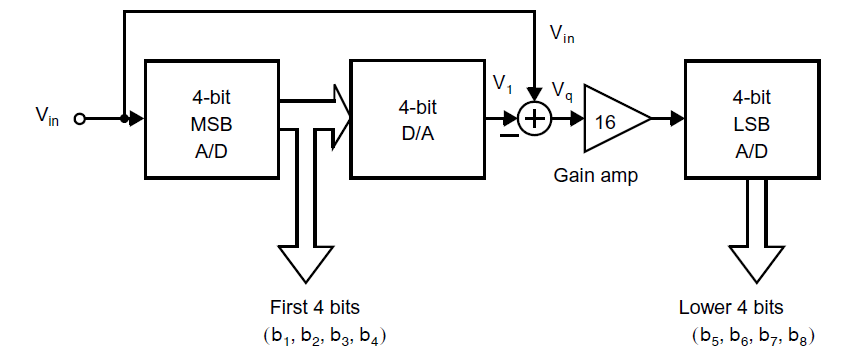
两步型ADC的结构图如下图所示：
实际上，两步型ADC可以被理解成仅有着两个流水级的特殊流水线ADC。上图的例子中展示了两个4 bit级，没有冗余位，组成了一个8 bit输出，4 bit MSB ADC决定了高4位的MSB。为了确定剩余的LSB，量化误差（残差）通过用4 bit DAC将4 bit数字信号转换成模拟值后与输入信号值相减。为了降低对查找剩余LSB的电路的要求，量化误差首先使用增益放大器放大16倍，然后LSB再用4 bit LSB ADC来决定。通过这种方式，相比8 bit的Flash ADC需要使用256个比较器，在两步ADC中仅仅需要使用32个比较器。但是，这种直接的方式会要求所有组件至少具备8 bit的准确性。为了显著减小对于4 bit MSB ADC的精度要求，一般会使用数字错误修正电路。
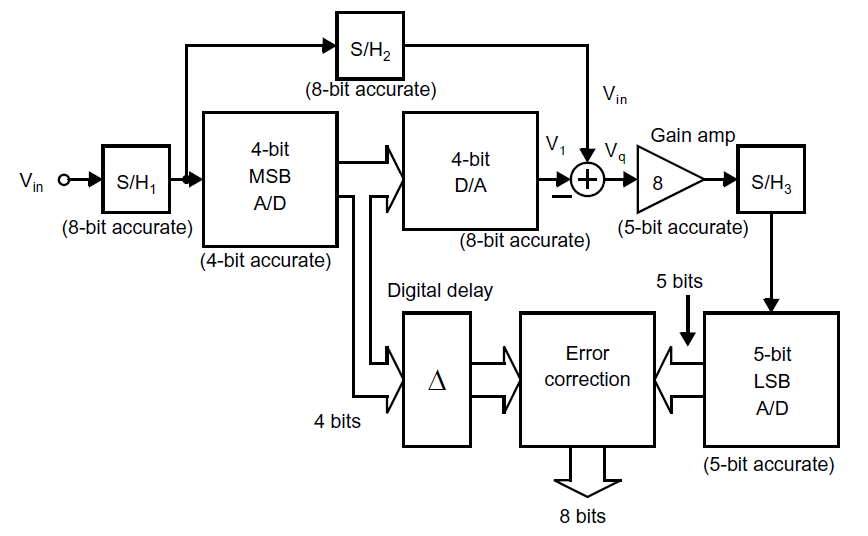
带有数字修正电路的两步型ADC的架构图如下图所示：
其操作类似于流水线ADC中的1.5 bit每级架构。4 bit和5 bit级之间有重合，因此在第一个ADC中的不精确可以通过第二级来抵消。为了理解这种修正如何工作，以及为什么需要一个5 bit的第二级（而不是4 bit），考虑一个理想ADC总的量化错误，定义\(V_{LSB}=V_{ref}/2^8\)（经常用于8 bit精度），我们有理想8 bit ADC：
然而，对于非理想8 bit ADC：
换而言之，量化信号最大情况下是理想值的两倍。
类似的，对于理想4 bit ADC来说（\(V_{LSB}\)仍然用8 bit的定义）：
因此在理想情况下，\(V_q\)的值（到8 bit精度）可以使用4 bit ADC来确定，因为\(V_q\)肯定是在\(16V_{LSB}\)以内的。但是，对于4 bit非理想MSB ADC来说，其绝对精度为\(8V_{LSB}\)，\(V_q\)的上下界范围为\(32V_{LSB}\)。因此，在非理想4 bit MSB ADC的情况下，必须要使用一个5 bit的LSB ADC，否则\(V_q\)会超出范围。注意8倍的增益放大器是用于将量化噪声重新放大回最大的信号电平来减小对5 bit LSB ADC的要求。最后，为了确定\(V_{in}\)，我们可以看到\(V_q\)的数字值在\(0.5V_{LSB}\)以内，而\(V_1\)的数字值有着相同的精度，因为我们假定了DAC有着8 bit精度，并且施加在DAC上的数字值已知。因此我们可以有：
具体来说，\(V_{in}\)可以通过合理的组合\(V_1\)和\(V_q\)的数字等效来获得。
总结来说，MSB ADC只需要精确到\(1/2^4=1/16\)。唯一需要达到8 bit \(0.5LSB\)精度的组件是两个采样保持电路和DAC以及减法电路。对于具体处理一个两步型ADC的例子，可以参考这个10 bit \(75MHz\)的实现[Petschacher,1990]。
除了采样保持电路的难度之外，另一个主要的限制是设计一个高速且精确（在5 bit下达到\(0.5LSB\)精度）的增益放大器。事实上，由于在高速电路中实现增益的难度，一般来说在第一级会使用更少的比特来降低对放大的需求。例如，一个在第一级仅仅分辨1 bit的两步型ADC可以得到非常低的功耗[Verbruggen, 2009]。
