模拟集成电路设计系列博客——7.5.2 周期型ADC

7.5.2 周期型ADC

周期型ADC（或者叫算数ADC）与逐次比较型ADC的工作原理很像，但是与逐次比较型ADC每次减半参考电压不同，周期型ADC每次保持参考电压不变，而将误差电压放大两倍。一个有符号周期型ADC的流程图如下图所示：

周期型ADC的结构图如下图所示[McCharles, 1977; Li, 1984]：

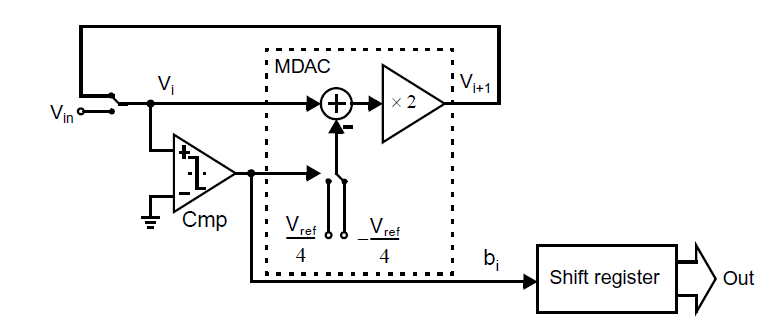
这个转换器只需要少量的模拟电路，因为其在转换时间内一直在重复使用相同的电路。

实现一个高精度的周期型ADC的难度在于构建一个精确的乘以二倍增益电路。幸运的是，如果乘以二操作用4个时钟周期的话，实现这一增益放大器，可以使得电路不再依赖任何电容匹配。乘以二增益放大器的操作如下图所示：

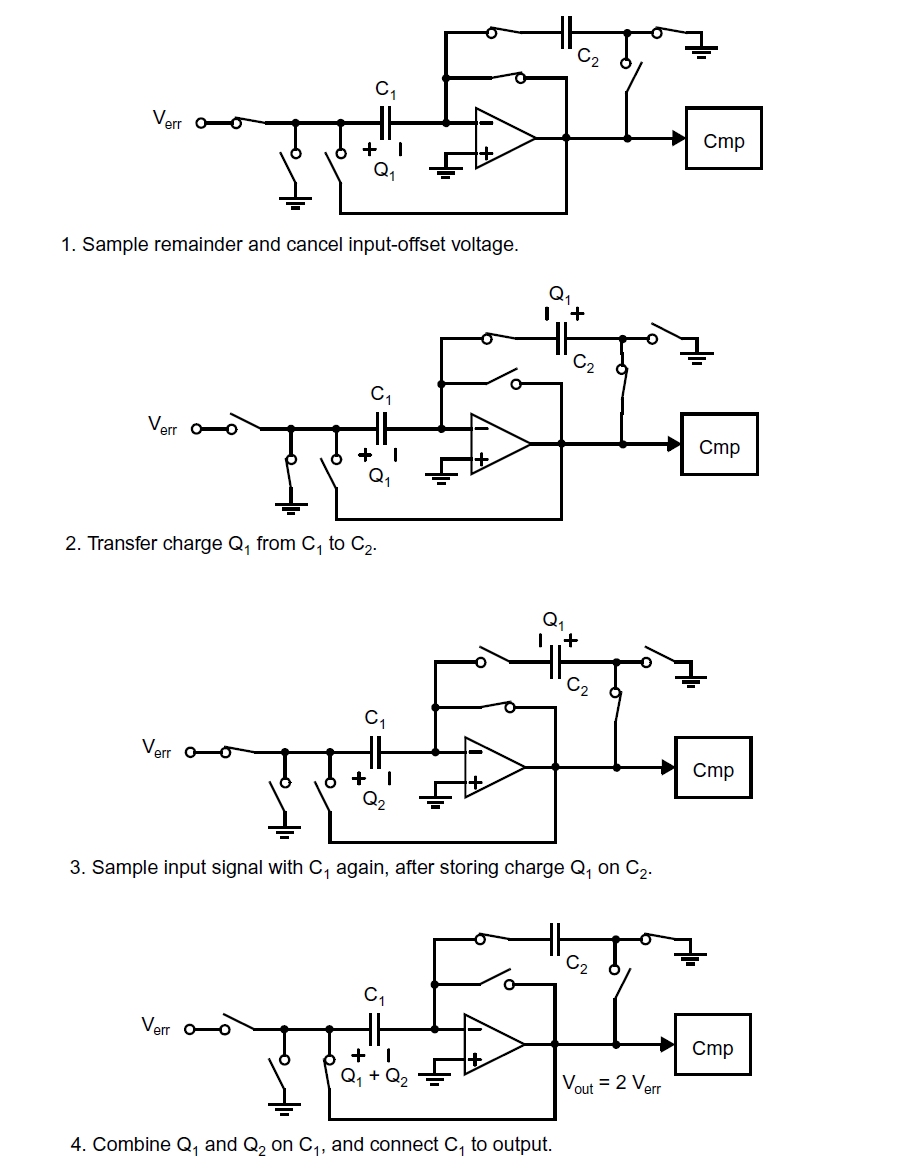
尽管这个电路用单端电路表示以供简化，单实际电路中一般会使用全差分电路。

这个增益放大器的基本思想是使用相同的电容对输入信号采样两次。在第二次采样时，第一个电容的电荷会被存储在第二个其容值不重要的电容上。在第二次采样后，两次的电荷被重新组合到第一个电容上，随后其被连接到放大器的输入和输出之间。

例题：

考虑上图中的乘以二增益电路，假定放大器的输入失调为\(V_{off}\)，求出每个阶段中的\(V_{C1}\)，\(V_{C2}\)和\(V_{out}\)。

解答：

在第一阶段，放大器输出连接到放大器的负输入端，有：

\[V_{out}=V_{off} \tag{7.5.11} \]

而两个电容两端的电压为：

\[V_{C1}=V_{err}-V_{off} \tag{7.5.12} \]

\[V_{C_2}=0-V_{off}=-V_{off} \tag{7.5.13} \]

在第二阶段的结尾，我们有：

\[V_{C1}=0-V_{off}=-V_{off} \tag{7.5.14} \]

这意味着其电容该变量为：

\[\Delta Q_{C1}=C_1(V_{err}-V_{off}-(-V_{off}))=C_1V_{err} \tag{7.5.15} \]

所有的电荷都被移动到\(C_2\)，从而有：

\[V_{C2}=-V_{off}+\frac{C_1}{C_2}V_{err} \tag{7.5.16} \]

并且\(V_{out}=(C_1/C_2)V_{err}\)。

在第三阶段的结尾，\(V_{C2}\)保持不变，因为其一侧为开路。同时，\(V_{C1}=V_{err}-V_{off}\)以及\(V_{out}=V_{off}\)和第一阶段一样。

最后，在第四阶段结束时，\(C_2\)被放电到和第一阶段相同的值，使得\(V_{C2}=-V_{off}\)，其电容的改变为：

\[\Delta Q_{C2}=C_2(\frac{C_1}{C_2})V_{err}=C_1V_{err} \tag{7.5.17} \]

所有的电荷又回到\(C_1\)，使得：

\[V_{C1}=2V_{err}-V_{off} \tag{7.5.18} \]

而输出电压会是所需的\(V_{out}=2V_{err}\)。注意最终的转换结果独立于\(C_1\)，\(C_2\)的尺寸，以及\(V_{off}\)的失调值。